In this post I want to discuss the basic setup of the algoritms used in the spq-sigs project in an attempt to create a multi-programming-language post-quantum foundation aimed at key-reuse-by-design blockchains.

ECDSA and quantum computing

Most blockchains today use ECDSA for signing transactions. A neat little property of ECDSA allows the public key to be derived from the signature with a simple operation, so consider blockchains to be filled with public keys. In theory, once quantum computing reaches a certain scale, ECDSA private keys could be derived from ECDSA public keys within a practical timespan. Think somewhere in the hours up to months range. If we are to believe the marketing and press releases by some of the big players in the Quantum Computing space, this scale will be available within years, but even if we take these numbers with a grain of salt, we should expect someone to have access to sufficiently scaled quantum computing powers before the end of the decade.

We should however consider that there are multiple levels of thread regarding QC and ECDSA as used in blockchains.

Problems with ECDSA key-reusage as used in key-reuse-by-design utility blockchains.
Problems with ECDSA key-reusage in blockchains, where key-reuse is an omission in wallet implementation rather than a design choice.
Problems with ECDSA and the time-window between transaction first transmission and the transaction becoming final.

Examples of blockchains that suffer from the first type of problems are utility blockchains like HIVE, and core blockchain technologies like the FlureeDB blockchain based graph database. The prime example of a blockchain that suffers from the second type of problems is BitCoin. At this moment, almost all blockchains, with the exception of QRL suffer from the third type of problem.

Problem one IMHO is the most urgent of problems, and the problem spq-sigs aims at helping to address. The last problem appears to be the least urgent because of the time constrains involved with the attacks of this type.

Hash-based signatures as ECDSA replacement.

As QRL has already demonstrated, it is possible to create a blockchain using so called hash-based-signatures. Hash-based signatures though are in no way a drop-in replacement for ECDSA. Other than ECDSA, hash-based signatures aren't a one-size-fits-all solution. Different use cases require different dimensioning of the algorithms used. The signatures are much larger, the signing process is statefull, and last but not least, a signing key for making hash based signatures is a resource that can and will get exhausted through usage.

Key-reuse-by-design chains

The spq-sigs project aims to provide quantum resistant signatures specifically for key-reuse-by-design blockchains. The biggest difference between currency type blockchains and key-reuse-by-design utility chains is that the first could potentially use signing keys that are dimensioned for few-time or even one-time usage signing key. While QRL is a great chain in that it demonstrates the viability of hash-based signatures for blockchain technology. I personally think QRL hash-based signature technology is over-dimensioned for the task at hand. This is not the subject of this blog though. The important thing is that a signing key for key-reuse-by-design chains needs to implement are signing keys where a single signing key can sign hundreds of thousands up to possibly billions of signatures.
The spq-sigs project explicitly does NOT aim to be suitable or dimensioned appropriately for signing keys that will only be used one up to a few thousand times.

libsodium as-a-platform

Because spq-sigs aims to aid (key-reuse-by-design) blockchain eco-systems in moving towards hash-based signatures, supporting just one programming language isn't an option. Using different crypto libraries from different languages has issues too. Fortunately the brilliant libsodium library has language bindings in many languages and can serve as a kind of a crypto platform that spans multiple programming languages.

At this moment I'm (slowly) working on a C++ implementation of spq-sigs. Next on the list will be a backport to Python, a first proof of concept was done in Python without libsodium before the design was complete, so a backport to Python is the logical second step.

Other languages on the list to be implemented are:

And hopefully:

Monte

Monte is an object-capability language that has libsodium as dependency (but currently doesn't expose it's API). While I'm not sure it will end up being possible, I think it should be worth exploring given the added security properties a wallet in an o-cap language could potentially provide to a blockchain ecosystem.

The list of languages used to include other languages because this project started off as a project for HIVE specifically, but as the project no longer has any primary target platform (the HIVE crowd wasn't particularly receptive to the dhf-proposal ), I'm now choosing languages in a target-platform-agnostic way. The pressence of clojure on the list being the only exception, because of the fact that I make extensive use of FlureeDB in my day job, and would love to see FlureeDB support hash-based signatures in the future.

Multi-layer keys

Because of the specs needed for key-reuse-by-design, and both performance and size considerations, spq-sigs only supports multi-layer signing keys. The minimum number of levels is two and there currently is no defined upper limit. Use of more than say a dozen layers is not recommended. So how do multi-layer signatures work? In simple terms, we could have our account-level key dimensioned to for example sign up to 64 intermediate level keys. Each intermediate level key could be dimensioned to sign up to 512 message level keys, and every transaction level key, to be used to sign up to 1024 messages. This results in a multi-level key that can sign up to 33,554,432 transactions. This might be a decent fit for for example HIVE where my account level key would be bound to my @pibara identity, and if I end up with a new intermediate key roughly every year, I could live to 115 years old, doing well over a thousand transactions a day on the chain, what on HIVE most likely is much more than an average user needs. But then, if I was using the account for a bot, it might end up being insufficient. Dimentioning the layers is something that falls outside of the scope of the project. Every blockchain project considering spq-sigs use in the future should research typical and outlier usage and pick the appropriate layer dimensions.

It is important to note that the dimentions of the signing keys for spq-sigs are determined by two cross-layer numbers plus a per-layer number.

hashlength: The number of bytes to use as hashing primative length, salt length and the length of the atoms of (derived) entropy used by the signing key. Values from 16 up to 64 are allowed.
wotsbits: The number of bits to encode together in an n-bits one-time-signature. Values from 4 up to 16 are allowed.
merkleheight: The layer-specific height of the layer-key merkle tree. Valued from 3 up to 16 are allowed.

An example of numbers we could use for our HIVE example abouve could be:

hashlength: 24
wotsbits: 12
merkleheight:
- 6
- 9
- 10

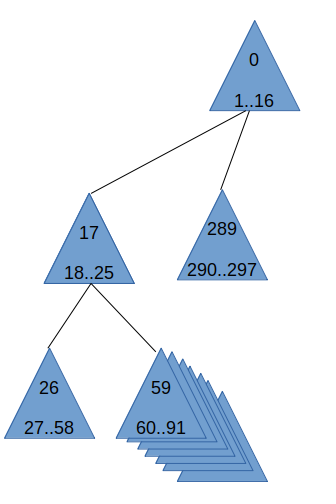
A simple key-index calculation algorithm

This part is rather new to the design of spq-sigs, but it is a bit of a game changer for the whole design. An earlier version of the disign, and the one currently still being used by the code at time of writing, extensively queried the libsodium entropy source for more entropy bits. That design choice was bas for multiple reasons. For one, it laid a burden of administration on the blockchain side of things, but secondly, it required the codebase to have a quite powerfull capability, from a capability perspective, to exaust a global source of entropy, what in general seems like a bad idea.

If we look at the libsodium documentation, we see a solution to both these problems. The key derivation functions. Like the rest of the core spq-sigs design, the crypto_kdf_derive_from_key consists of nothing but blake2b operations. The function needs a shared bit of high entropy data that can be created with the crypto_kdf_keygen function. For spq-sigs, this key will be our private key. Now the other thing that crypto_kdf_derive_from_key needs is a unique 64 bit number.

To do this, we need a little simple algorithm that fits with our multi-layer singing key setup. We start off with the account level key. This key, like every layer key, uses a key-generation-salt. We allocate number 0 for the index number for the salt for the upper level key. The upper level key also needs a lot of private-key data chunks. To determine just how many we:

Calculate the number of times we need to take wotsbits bits to make hashlength bytes. In our example, we have 24 byte hashlength and 12 wotsbits, so that would be exactly 16 times.
We multiply this number by two to get the number of high-entropy chunks we need per signature. In our case we get 32.
We take two to the power merkleheight, in our case 2^6, we get 64
We multiply the two numbers, in our case we get 32x64=2048

This means in our case, the account level key get a total of 2049 numbers to work with. 0 (for the salt) and 1..2048 (for the the private key chunks). The first of the intermediate level keys to get generated will start off at the next number: 2049 for the key-generation salt. Then the next 16384 ones (2050..18433) for the private key chunks.

Then for the transaction level key, we start off at the very next number, 18434, for the key generation salt. The next 32768 ones (18435..51202) for the private key chunks.

Now, after we have signed 1024 transaction with our transaction level key, it is time to replace the transaction level key with a new one. The salt for the next transaction level key will end up at the next unused index: 51202, and the next 32768 ones (51203..83970) for the private key chunks.

Our code uses a simple little algoritm for making sure the indices are allocated as described above.

Layer-key salt

In the above section we already discussed the use of the key-generation salt. What is it? It is basically a tiny bit of extra entropy used to make the underlaying hashing a tiny bit more secure by making it a bit less predictable. Because a signing key is multi layered and will be used to sign possibly millions of transactions, salting, or rather, hashing our salts with a key, can help to add just a tiny bit of extra security against potential rainbow table type attack factors.

The salt is currently used as follows:

As key in crypto_generichash_blake2b_init when generating or validating WOTS chains, when calculating the merkle tree and when combining the pubkey wots chunks into a per-signature hash.
As key in crypto_generichash_blake2b when hashing a message of transaction.

The importance of this salt depends greatly on the type of messages or transactions it gets used on. If there is something like a nonse in the message or transaction then this salt may be useless. The overhead though is limited and making it optional would complicate the design, so using the salt seems a decent addition to spq-sigs.

Double WOTS chains

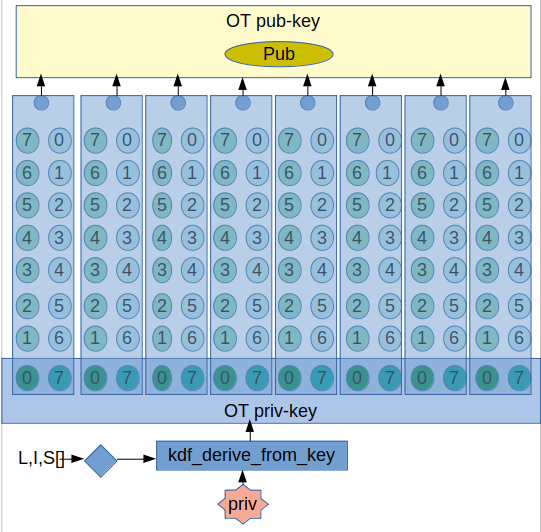
A WOTS chain is basically nothing more than a private-key chunk that gets hashed a number of times to create a public-key chunk. When now you want to sign a couple of bits (wotsbits bits), you take the number those bits represent, and hash the private key that many times. A validator can now take the signature chunk, hash it the remaining number of times, and arive at the public key. If the public key matches, all is fine.

But now imagine a man in the middle. A man in the middle that receives a signature for the bits 111 won't be able to do much, but what if it was 000 or 001? He could replace those bits in the message and create a valid updated signature.

XMSS as used in QRL has a solution for this using a checksum. Because we want our solution to be simple yet robust, we choose for a different and somewhat less compact solution: We use a double WOTS chain. So to sign 001, you will have one WOTS chain, the up WOTS chain do hash the up private key chunk one or 001 times, and we will have a second WOTS chain, the down wots chain where for signing we hash the down private key chunk 6 or 110 times. This means that the same MITM bit change attack can never be done in both WOTS chains.

So how does a signature with the double WOTS chains work?

Each whole signature has its unique index I
We take the hash of the transaction .
We chop up that hash into N chunks of wotsbits bits, each chunk has its unique sub-index S.
We take the value M of the bits of each chunk as the sub-value to sign.
Using I, S and the numbering algoritm above, we use crypto_kdf_derive_from_key to get an up and a down private key chunk
We hash the up private key chunk M times and the down private key chunk the complement of M times.
The resulting two values are our n-bits signature.
We concatenate all n-bits signatures into a transaction signature.
We prepend a merkle-tree header (see below)

One-time-signature key collections

The WOTS chains are simple, but how do we fit them toghether into a single level-key setup?

Well the first thing we do is we hash the up and down pubkey chunks into a single value. Then we do the same concattenating all of the sub-key chunks so we get a single hash for all the WOTS chains for a single signature. We considder these single hash values, for all of the potential signatures a level-key can make to be the level-key full-size pubkey.

A merkle tree of one time pubkeys

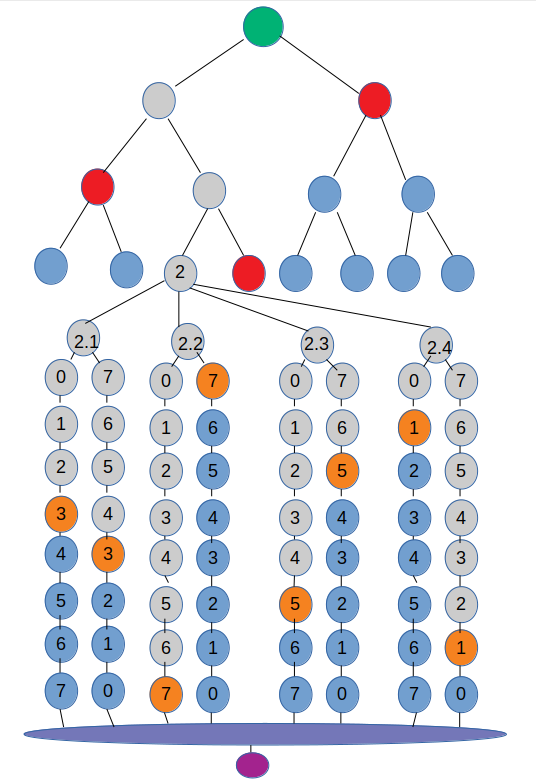
Now we get to the point where the level-keys concepts start to come together. We have a merkle tree that turns our full-size pubkey into a reduced-size pubkey. How this works is that we take the hash of each two consecurive pubkey chunks. Then we repeat the process untill there is only one hash value left, the merkle tree root, or reduced-size pubkey.

As we see in the image, our single small private key gets expanded to a huge private key made up of many hashlength long chunks
of high-entropy data. These are then combined in double WOTS chains to produce an equally large pubkey. That pubkey is then reduced to a smaller but still very large pubkey, that finaly in a merkle tree is reduced to a hashlength long public key.

Signature structure

So now for the signature for a single level. We look at the same image as above. In short, the green, red and orange dots form our one level signature. Using the orange and red dots, through the grey dots, the green dot can be reconstructed if the signature is valid.

The signature for a single level has the following stucture:

The level-key reduced-size pubkey (hashlen long)
The salt used during level-key creation (hashlen)
A merkle-tree header (all the red dots times hashlen)
The signature index (2 bytes)
The WOTS signature (all the orange dots times hashlen)

Full-signature structure

While it would be OK to just concatenate the different signatures needed to get the full chain from account-level pubkey to transaction signature covered, if we know the receiving end already has part of that chain, we could do with a compressed version instead.

compressed levels (one bytes, this will limit compressed levels to 256)
compressed entries
entries

The entries should have the form as described above. The compressed entries only hold the following fields:

The level-key reduced-size pubkey (hashlen long)
~~The salt used during level-key creation (hashlen)~~
~~A merkle-tree header (all the red dots times hashlen)~~
The signature index (2 bytes)
~~The WOTS signature (all the orange dots times hashlen)~~

Wallet-side pub-key caching

While just knowing the indices of the level keys is enough to reconstruct them, the reconstruction of all the WOTS chains at every start up isn't desireable for performance reasons. For this reason, the wallet is expected to cache the lowest level nodes of the merkle tree.

Chain-side indices

While it might seem logical to remember the indices used in signing on the client side, there would be drawbacks to that approach if the user has a wallet on multiple divices and wants these to effectively be the same wallet. For this reason, spq-sigs will not itself facilitate in storing client side indices as it assumes indices to be stored and retreivable from some chain-side API.

Wallet encryption (to-do)

This part isn't designed yet. It is important for the libraries to facilitate posibilities for the secure password protected storage of the private key. Libsodium provides us with Argon2, Xsalsa20 and Poly1305 that together seem like good candidates for encrypting the private part of the signing key. This part though hasn't really be looked at.

Status

At this point in time the key-index calculation code has been tested seperately, but has not yet been integrated into the code-base. Doing so is currently the first priority. For the rest of it, for C++ this is the current prioritized todo list:

Integrate key-index calculation code
Update the API to better match key-index calculation code
Code-cleanup
Implement signing key restore (with and without provided pubkey data)
Implement signature serialization/deserialization
Private key password protection
Final code cleanup and RC1 version.

Note that a 1.0 version won't get released untill a Python backport has been completed and interoperability has been close to 100% validated.

List of github repos

C++ : Currently active, working towards Minimal Viable Project
Python : Currently holding Proof-Of-Concept code predating C++ implementation. Backporting as soon as C++ repo reaches MVP status.
JavaScript : Next in line after the Python backport.
Monte : Research needed first, promising little ocap language.
Rust: Not any time soon, but definetely comming.
Clojure: Not soon. Rust comes first. Awaiting what FlureePBC is up to.
Elixir: This one might be a while. No github repo yet.

Support this project.

If you would like to support the spq-sigs project, please check out my crypto tipping jar. This is currently a slow moving hobby project without any structural time allocated to it by me. Tips could allow me to allocate structural time to the project and speed things up a bit.

A walkthrough of Simple-Post-Quantum-Signatures (spq-sigs)