🇮🇹 VERSIONE ITALIANA 🇮🇹
Capitoli anteriori:
1. Gli inuit
2. La verità
3. Metodo scientifico
4. La crisi della riproducibilità
Immaginate di giocare a dadi, vi esce fuori un 1️⃣ 10 volte di fila e sospettate che i dati possano essere truccati.
Ricordate la falsificabilità?
Se voglio provare che qualcosa (ipotesi alternativa) è vera devo provare anche che il contrario (ipotesi nulla) è falso.
Se tutti gli uomini sono mortali è vero, devo anche provare che tutti gli uomini sono immortali è falso. Trovare un solo immortale renderebbe vera l'ipotesi nulla e quindi falsa quella alternativa.
Torniamo ai dadi, se voglio provare che la mia ipotesi alternativa, i dadi sono truccati, è vera, devo anche provare che l'ipotesi nulla, il contrario, i dadi non sono truccati è falsa.
Come faccio?
Ogni volta che lancio un dado, la probabilità di ottenere un 1️⃣, o qualsiasi altro numero, è di 1/6.
Tendiamo a pensare che se ho lanciato un 1️⃣ 5 volte di fila la probabilità che io tiri un numero diverso nel prossimo lancio è più alta, ma è la stessa, in quanto si tratta di eventi indipendenti.
Ciò che diminuisce è la probabilità di ottenere un 1️⃣ due volte di fila, sarebbe di 1/32, e 1/216 se li lanciamo 3 volte.
Se ci annoiamo e abbiamo la pazienza di lanciare i dadi moltissime volte e annotiamo quante volte esce il nostro 1️⃣ ogni 1000 tiri, per esempio, vedremo che la maggior parte delle volte l'1️⃣ viene fuori 167 volte, che è il 16,6% di probabilità che ci aspettavamo.
Se abbiamo la pazienza di lanciare il dado moltissime volte ancora sarebbe possibile arrivare a lanciare un 1️⃣ per 1000 volte di seguito, per quanto improbabile sia, e potete immaginare che questo possa essere giustificato con il caso. Se questo dovesse succederci nel primo round di 1000 tiri, anche aumentando i nostri sospetti iniziali che i dadi siano truccati, non ce lo confermerebbe con una certezza del 100%.
E se ci succedesse in più round?
Come stabilire quando i risultati sono statisticamente significativi e non dovuti al caso?
Per questo gli statistici usano il p-value, o il valore minimo di probabilità per rifiutare l'ipotesi nulla (che nel nostro esempio è il dado non è truccato).
Non rientra nell'ambito di questo post spiegare i calcoli del valore p, poiché per la loro valutazione dovremmo includere molte altre variabili, che vanno al di là delle mie conoscenze.
Per semplificare, se distribuiamo in un grafico quante volte ho ottenuto un 1️⃣ per ogni 1000 tiri, osserveremo una curva gaussiana come questa nell'immagine qui sotto, dove al centro osserveremo 167, il caso più frequente, e nel nostro estremo, il caso più improbabile, che otteniamo un 1️⃣ ogni volta.
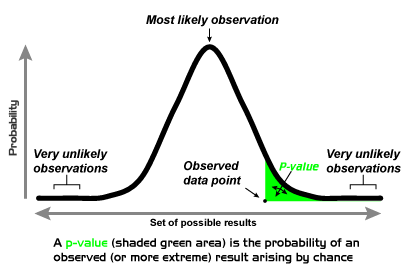
Quest'area di casi più improbabili alle estremità della curva, segnata in verde sul grafico, rappresenta questi eventi che presumibilmente non sono dovuti al caso, come ottenere un 1️⃣ ad ogni lancio, e il limite tra ciò che è statisticamente significativo e ciò che non lo è, è il p-value, che deve essere inferiore a 0,05.
Se invece di lanciare i dadi in gruppi di 1000, li lanciamo almeno 532 volte in gruppi di 3, come nell'esempio precedente, dovrebbe uscirci un triple 1️⃣ almeno 2 volte in termini di probabilità, e non ci sarebbe nulla di anormale. In questo caso il p-value sarebbe > 0,05 e la nostra ipotesi di dadi truccati verrebbe scartata, anche se potrebbero esserlo, il p-value indica semplicemente che non ci sono abbastanza indizi per farci sospettare qualcosa al di fuori dal normale.
Spero di non avervi confuso di più, l'intenzione è quella di rendere i concetti più semplici.

Ora ricordate che questa non è l'epoca di Newton e non staremmo lanciando mele o dadi e calcolando i risultati e le probabilità a mano.
Avremmo un computer che lancia costantemente dadi e registra i risultati.
E cerca i patterns che gli indichiamo.
Ad esempio, tutti i set di dati che hanno un p-value < 0,05, che è un valore fissato arbitrariamente per consenso nella comunità scientifica.
Ebbene questo può essere stato il caso qualche anno fa, ma oggi abbiamo sensori che ci inviano dati da analizzare sul mondo fisico, sui nostri comportamenti o sulle nostre preferenze in continuazione.
Abbiamo anche algoritmi che non solo cercano i modelli che noi gli indichiamo, ma imparano anche a riconoscere modelli che sarebbero invisibili all'occhio umano.
Ma andiamo, con calma, di questo ne parleremo in un altro capitolo.
Ricorderete dal precedente capitolo, sulla crisi della riproducibilità, che alcuni ricercatori hanno citato la pressione per pubblicare come possibile causa.
Pressione che può tradursi in bias nel cercare di vedere anomalie dove non ce ne sono.
Il p-value passa dall'essere un indicatore dell'affidabilità delle conclusioni ad essere un obiettivo.
Quando una misura diventa un obiettivo, cessa di essere una buona misura.
Legge di Goodhart
La tecnica del p-hacking si riferisce alla manipolazione dei dati, non sempre in malafede, eliminandone alcuni, aumentando la frequenza o smettendo di misurare quando ci si avvicina al limite di ciò che è statisticamente significativo.
Proviamo.
Già che siamo nel periodo giusto, immaginate di essere uno scienziato che crede che l'economia degli Stati Uniti sia influenzata dal governo dei repubblicani o i democratici .
In questa pagina è possibile analizzare i dati reali dal 1948.
Potete scegliere di esaminare solo i dati sulla disoccupazione in base al presidente in carica, o alle materie prime e ai governatori o senatori in carica.
Giocate con i dati fino ad ottenere un p-value < 0,05 e i vostri risultati saranno statisticamente significativi per essere pubblicati su una rivista scientifica.
Io ho già ottenuto la gloria scientifica, ho appena scoperto che i presidenti democratici hanno un effetto positivo sull'economia in termini di disoccupazione e di prezzi delle materie prime con un p-value di 0,03.
Ma se aggiungo ai dati dei presidenti quelli dei governatori democratici l'effetto sull'economia è negativo, ed è anch'esso un risultato statisticamente significativo con un valore p di 0,01.
Hack Your Way To Scientific Glory
Così posso giocare finché non trovo i dati che fanno per me.

Questo non significa che si voglia barare di proposito, solo che, già conosciamo gli umani, a volte ci ostiniamo a vedere quello che vogliamo vedere senza rendercene neanche conto, raccontandoci una bugia a noi stessi.
Ciò non solo non è corretto, ma nemmeno sbagliato!
Wolfgang Pauli
(Si tratta di una frase un po' sprezzante sulla pseudo-scienza, non è nemmeno sbagliato, nel senso che non è nemmeno falsificabile)
La questione del p-hacking è spiegata semplicemente in questo comic.
Immaginate che io voglia dimostrare che le gelatine verdi causano l'acne.
Posso dimostrare con un p-value inferiore a 0,05 che quelle nere, rosse, gialle, rosa, bianche, marroni, arancioni non producono acne, l'ipotesi nulla.
Basta questo a dimostrare che quelle verdi non producono acne?
Beh, se mi astengo dal testare l'effetto delle caramelle gommose verdi...
Ovviamente si tratta solo di una semplificazione, in alcuni casi come i dadi o le gelatine la fallacia nel ragionamento è evidente, ma nel caso di esperimenti che coinvolgono molti dati e variabili può non esserlo così tanto.
Per cercare di minimizzare queste pratiche e i loro effetti sull'affidabilità degli studi scientifici, l'American Statistical Association (ASA) ha elaborato sei principi per incoraggiare il corretto uso e l'interpretazione del p-value:
- I p-value possono indicare quanto i dati siano incompatibili con un modello statistico specifico.
- I p-value non misurano la probabilità che l'ipotesi oggetto di studio sia vera, né la probabilità che i dati siano stati prodotti solo per caso.
- Le conclusioni scientifiche e le decisioni aziendali o politiche non dovrebbero basarsi esclusivamente sul fatto che un p-value superi una determinata soglia.
- Una corretta illazione richiede piena trasparenza e informazione.
- Il p-value, o significato statistico, non misura la dimensione di un effetto o l'importanza di un risultato.
- Di per sé, un p-value non fornisce una buona misura di evidenza rispetto a un modello o a un'ipotesi.
P-ValueStatement

Il problema, come ho detto, non è necessariamente dovuto alla malafede degli scienziati.
Con il crescente numero di dati che gestiscono, sono necessarie conoscenze sempre più avanzate in materia di scienza dei dati e di statistica, di cui probabilmente non dispongono a sufficienza alcuni professionisti di diverse discipline, come dimostrato da questi studi.
I risultati suggeriscono che gli studenti e i professori universitari non conoscono la corretta interpretazione del p-value. L'errore di probabilità inversa presenta maggiori problemi di comprensione. Inoltre, c'è confusione sulla significatività statistica e sulla significatività pratica o clinica. Questi risultati evidenziano la necessità di un'educazione statistica e di una rieducazione statistica.
Fallacie sul p-value condivise da professori e studenti
José Niz-Ramos, in Le fallacie della p e significazione statistica, su 25 studi analizzati, conclude:
Il concetto del p-valuel non è semplice, ha diverse fallacie e interpretazioni errate che devono essere considerate per evitarle il più possibile. Si consiglia di non utilizzare il termine "statisticamente significativo" o "significativo", sostituendo la soglia di 0,05 con quella di 0,005, riportando p-value accurati con il 95% di CI, rischio relativo, apporto di probabilità, dimensione o potenza dell'effetto e metodi bayesiani.
Propone inoltre una serie di misure per affrontare il problema:
- Sostituire la soglia di p = 0,05 con p = 0,005 e indicare i valori compresi tra 0,05 e 0,005 come suggestivi.
- Fatevi consigliare da esperti di statistica per interpretare i risultati della ricerca scientifica.
- Ribadire l'importanza clinica dello studio e fornire dichiarazioni chiare ed esplicite delle domande e delle ipotesi di ricerca da testare.
- Dettaglio della metodologia dell'analisi statistica (giustificazione della dimensione del campione e motivazioni dell'uso dei metodi statistici) Se vengono utilizzati i valori NHST e p, devono giustificare la loro applicazione.
- Incoraggiare i revisori delle riviste e i comitati editoriali a non permettere l'uso della frase "statisticamente significativo" o "significativo".
- Sottolineare che gli abstract devono contenere risultati con valori numerici (tassi, percentuali, proporzioni) degli effetti dimostrati.
- Segnalare valori p precisi (non meno di 0,05 o 0,01), anche se esatti, ad esempio 0,002, utilizzando indici di prova aggiuntivi: 95% CI, rischio relativo, rapporto di probabilità (odds ratio), dimensione o potenza dell'effetto e metodi bayesiani.
Il tema dei dati è molto denso, in questo capitolo abbiamo visto solo un aspetto dell'enorme sfida che esso pone alla nostra società moderna, dal punto di vista del progresso scientifico.
Nel prossimo capitolo esploreremo alcune questioni e sfide dei dati in economia.
Alla prossima volta!
Baci, !BEER e abbracci 😘 🍻 🤗

🇪🇸 VERSIÓN ESPAÑOLA 🇪🇸
Capitulos anteriores:
1. Los inuit
2. La verdad
3. Método científico
4. La crisis de la reproducibilidad
Imaginen que están jugando a los dados, le ha salido un 1 10 veces seguidas y sospechan que están trucados.
¿Se acuerdan de la falsabilidad?
Si quiero demostrar que algo (hipótesis alternativa) es verdadero tengo que demostrar también que lo contrario (hipótesis nula) es falso.
Si todos los hombres son mortales es verdadero, también tengo que demostrar que todos los hombres son inmortales es falso. Encontrar uno solo inmortal haría que la hipótesis nula sea verdadera y por tanto la alternativa falsa.
Volvemos a los dados, si quiero demostrar que mi hipótesis alternativa, los dados están trucados, es verdadera, tengo que demostrar también que la hipótesis nula, lo contrario, los dados no están trucados es falsa.
¿Cómo lo hago?
Cada vez que tiro un dado la probabilidad que me salga un 1️⃣, o cualquier otro numero, es de 1/6 cada vez.
Tendemos a pensar que si me ha salido un 1️⃣ 5 veces seguidas la probabilidad de que me salga un numero diferente sea más alta, pero es la misma, al ser sucesos independientes.
Lo que sí disminuye es la probabilidad que saquemos un 1️⃣ dos veces seguidas sería, de 1/32, y 1/216 si los lanzamos 3 veces.
Si nos aburrimos y tenemos paciencia de tirar los dados muchísimas veces y anotar cuantas veces sale nuestro 1️⃣ cada 1000 tiros por ejemplo, veremos que la mayoría de las veces ha salido 167 veces, que es la probabilidad del 16,6% que nos esperábamos.
Si tenemos paciencia de lanzar los dados muchas veces sería posible obtener hasta un 1️⃣ las 1000 veces seguidas, por muy improbable que sea, y imaginarán que esto puede ser justificable con el mismo azar. Si esto nos pasara en la prima ronda de 1000 tiros, aun aumentando nuestras sospechas iniciales de que los dados están trucados, no non los confirmaría con un 100% de seguridad.
¿Y si nos pasara en más rondas?
¿Cómo establecemos cuándo los resultados son estadísticamente significativos y no se deben al simple azar?
Para esto los estadísticos utilizan el p-value, o el valor mínimo de probabilidades para rechazar la hipótesis nula (que en nuestro ejemplo es los dados no están trucados).
No entra en las finalidades de este post explicar los cálculos del p-value, ya que para su evaluación deberíamos incluir muchas otras variables, y escapan de mi alcance.
Para simplificar, si distribuimos en un grafico cuantas veces me ha salido un 1️⃣ en cada tanda de 1000, observaremos una curva gaussiana como esta de la imagen abajo, donde en el centro observaríamos el 167, el caso más frecuentes, y en nuestro extremo, el caso más improbable, que nos salgan 1️⃣ todas las veces.

Esta área de casos más improbables en los extremos de la curva, marcada en verde en el grafico, representan estos casos que supuestamente no se deben al azar, como que me salga un 1️⃣ todas las veces, y el limite entre lo que es significativo estadísticamente y lo que no lo es, es el p-value, que tiene que ser inferior a 0,05.
Si en lugar de lanzar los dados en grupos de 1000, los lanzamos mínimo 532 veces en grupos de 3, como en el ejemplo anterior, nos tendía que salir un triple 1️⃣ mínimo 2 veces en términos de probabilidad, y no tendría nada de anormal. En este caso el p-value sería > 0,05 y se descartaría nuestra hipótesis de dados trucados, aunque puedan serlo, simplemente el p-value nos indica que no hay suficientes indicios que nos hagan sospechar de algo fuera de lo normal.
Espero no haberos liado más, la intención es render los conceptos más sencillos.

Ahora recuerden que no estamos en la época de Newton y nosotros tampoco nos dedicaríamos a lanzar manzanas o dados y anotar resultados y calcular probabilidades a mano.
Tendríamos un ordenador que sin parar lanza dados y anota los resultados.
Y busca los patrones que nosotros le indiquemos.
Por ejemplo todos los conjuntos de datos que tengan un p-value < 0,05, que es un valor establecido arbitrariamente por consenso en la comunidad científica.
Bueno, esto puede que fuera así hace unos años, pero hoy tenemos sensores que nos envían datos que analizar del mundo físico, de nuestras conductas o preferencias en continuación.
También tenemos algoritmos que no solo buscan los patrones que nosotros les indiquemos, sino que aprenden solos a reconocer patrones que al ojo humano serían invisibles.
Pero vamos con calma, de esto hablaremos en otro capitulo.
Recordarán del capitulo anterior sobre la crisis de la reproducibilidad y que algunos investigadores citaban la presión para publicar.
Presión que se puede traducir en sesgo al intentar ver anomalías donde no las hay.
El p-value pasa de ser un indicador de la fiabilidad de las conclusiones a ser un objetivo.
Cuando la medición se convierte en un objetivo, deja de ser una buena medición.
Ley de Goodhart
La técnica del p-hacking se refiere a la manipulación de los datos, no siempre en mala fe, eliminando algunos, aumentando la frecuencia o parando de medir cuando se está cerca del limite de lo estadísticamente significativo.
Vamos a probarlo.
Ya que estamos en época, imagina que eres es un científico que cree que la economía de EE.UU. se ve afectada si los republicanos o los demócratas gobiernan.
En esta pagina puedes analizar datos reales desde el 1948.
Puedes elegir si quieres examinar solo los datos de desempleo en función del presidente en cargo, o de materias primas y los gobernadores o senadores en cargo.
Juega con los datos hasta que obtengas un p-value < 0,05 y tus resultados serán estadísticamente significativos para ser publicados en una revista científica.
Yo ya me he abierto paso en la gloria científica, acabo de descubrir que los presidentes demócratas tienes un efecto positivo sobre la economía en termino de desempleo y precios de materias primas con un p-values de 0,03.
Pero si añado los datos de presidentes y gobernadores demócratas el efecto sobre la economía es negativo, y también es un resultado estadísticamente significativos con un p-value de 0,01.
Hack Your Way To Scientific Glory
Así puedo jugar hasta que encontrar los datos que me convengan.

Eso no quiere decir que uno quiera hacer trampas adrede, solo que ya conocen los humanos, a veces nos obstinamos en ver los que queremos ver sin darnos cuenta, contándonos una mentira a nosotros mismos.
No solo no es correcto, ni siquiera es falso.
Wolfgang Pauli
(Se trata de una frase un poco despectiva sobre la pseudo-ciencia, entendiendo por falso, que nis siquiera es falsable.)
La cuestión queda muy bien explicada en este comic.
Imaginen que quiero demostrar que las gominolas verdes producen acné.
Puedo demostrar con un p-value inferior a 0,05 que las negras, rojas, amarillas, rosa, blancas, marrones, naranjas no producen acné, la hipótesis nula.
¿Es suficiente esto para demostrar que las verdes no producen acné?
Bueno, si me abstengo de testar el efecto de las gominolas verdes...
Evidentemente este es solo una simplificación, en algunos casos como los dados o las gominolas la falacia en el razonamiento es evidente, pero en el caso de experimentos en los que intervienen muchos datos y variables puede no ser tan evidente.
Para intentar minimizar estas practicas, y sus efectos la fiabilidad de los estudios científicos la American Statistical Association (ASA) ha redactado seis principios para fomentar el uso e interpretación adecuados del p-value:
- Los valores P pueden indicar cuán incompatibles son los datos con un modelo estadístico específico.
- Los valores P no miden la probabilidad de que la hipótesis estudiada sea cierta, ni la probabilidad de que los datos se hayan producido sólo por azar.
- Las conclusiones científicas y las decisiones empresariales o políticas no deben basarse únicamente en si un valor p supera un umbral específico.
- La inferencia adecuada requiere una total transparencia e información.
- El valor p, o significación estadística, no mide el tamaño de un efecto o la importancia de un resultado.
- Por sí mismo, un valor p no proporciona una buena medida de la evidencia con respecto a un modelo o hipótesis.
P-ValueStatement

El problema como decía no necesariamente se debe a una mala fe de los científicos.
Con el numero creciente de datos que manejan, los big-data, se necesitan siempre más conocimientos avanzados de ciencia de datos y estadística que probablemente se le quedan cortos a algunos profesionales de diferentes disciplinas como se evidencia en estos estudios:
Los hallazgos sugieren que los estudiantes y profesores universitarios no conocen la interpretación correcta del valor p. La falacia de la probabilidad inversa presenta mayores problemas de comprensión. Además, se confunde la significación estadística y la significación práctica o clínica. Estos resultados destacan la necesidad de la educación estadística y re-educación estadística.
Falacias_sobre_el_valor_p_compartidas_por_profesores_y_estudiantes_universitarios

José Niz-Ramos, en Las falacias de la p y significación estadística, sobre 25 estudios analizados concluye:
El concepto del valor de p no es simple, tiene varias falacias y malas interpretaciones que deben considerarse para evitarlas en lo posible. Se recomienda no usar el término “estadísticamente significativo” o “significativo”, sustituir el umbral de 0.05 por 0.005, informar valores de p precisos y con IC 95%, riesgo relativo, razón de momios, tamaño del efecto o potencia y métodos bayesianos.
También propone una serie de medidas para enfrentar el problema:
- Sustituir el umbral de p = 0.05 por p = 0.005 y referir los valores entre 0.05 y 0.005 como sugerentes.
- Asesorarse de expertos en estadística para interpretar los resultados de una investigación científica.
- Reiterar la importancia clínica del estudio y proporcionar enunciados claros y explícitos de la(s) pregunta(s) de investigación y la(s) hipótesis(s) que se comprobarán.
- Detallar la metodología del análisis estadístico (justificación del tamaño de la muestra y razones del empleo de métodos estadísticos). Si utilizan NHST y valores de p deberán justificar su aplicación.
- Incitar a los revisores y consejos editoriales de las revistas para no permitir el uso de la frase “estadísticamente significativo” o “significativo”.
- Recalcar que los resúmenes contengan resultados con valores numéricos (tasas, porcentajes, proporciones) de los efectos demostrados.
- Informar valores de p precisos (no menores de 0.05 o 0.01), incluso exactos, por ejemplo 0.002, utilizando índices de evidencia adicionales: IC95%, riesgo relativo, razón de momios (odds ratio), tamaño del efecto o potencia, y métodos bayesianos.
El tema de los datos es muy denso, en este capitulo solo hemos visto un aspecto del enorme desafío que supone para nuestra sociedad moderna, desde el punto de vista del progreso científico.
En el próximo capítulo exploraremos algunas cuestiones y desafíos de los datos en economía.
Hasta la próxima!
Besos, !BEER & abrazos 😘 🍻 🤗

Bellissimo post come sempre cara @maruskina che bello vedere i tuoi post su Olio di Balena
Baci, !BEER & abbracci 😘🍻🤗Grazie mille @zottone444!
Grazie a te di tutte le beer, se continuo cosi mi ubriaco
View or trade
BEER.BEERHey @zottone444, here is a little bit of from @maruskina for you. Enjoy it!Learn how to earn FREE BEER each day by staking your
BEER.Su post ha sido valorado por @ramonycajal
Muchas gracias!!!
Besos, !BEER & abrazos
View or trade
BEER.BEERHey @ramonycajal, here is a little bit of from @maruskina for you. Enjoy it!Learn how to earn FREE BEER each day by staking your
BEER.Vimos su tweet usando #HiveFixesEsta etiqueta, apreciamos su apoyo contra el tema de la censura.
Por cierto, te invito también a unirte a nuestra comunidad aquí. Un grupo que se dedica a estudiar las palabras de Dios a través de las enseñanzas del hermano Eli Soriano. ¡Pregúntele al hermano Eli, la Biblia responderá!
Dios le bendiga 😇😍
👇👇👇
https://peakd.com/c/hive-182074/created
Muchas gracias!!!
Besos !BEER, & abrazos
View or trade
BEER.BEERHey @fatimajunio, here is a little bit of from @maruskina for you. Enjoy it!Learn how to earn FREE BEER each day by staking your
BEER.Congratulations @maruskina! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s) :
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @hivebuzz:
Your post has been voted as a part of Encouragement program. Keep up the good work!
Dear reader, follow and support this author, Install Android: https://android.ecency.com, iOS: https://ios.ecency.com mobile app or desktop app for Windows, Mac, Linux: https://desktop.ecency.comLearn more: https://ecency.com Join our discord: https://discord.me/ecency