
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH
04-02-2025 - Analytic geometry - Gauss-Jordan elimination [EN]-[IT]
With this post I would like to give a short instruction about the topic mentioned in the subject
(code notes: X_88)
***Gauss-Jordan elimination ***
This method is a variant of the Gauss elimination method
Let's proceed with an example and take the following matrix:
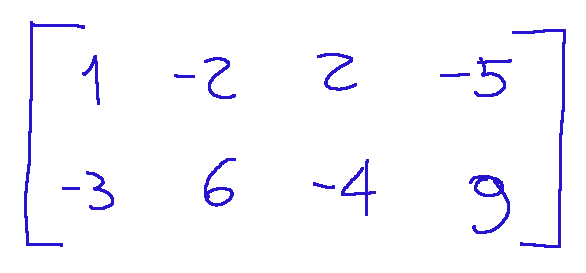
Now let's apply the Gauss-Jordan method
Step 1
Elimination of the first element of the second row
The first pivot is already 1 in position (1,1), then we use the first row to eliminate the -3 in position (2,1) by making R2=R2+3R1
we will get the following simplification
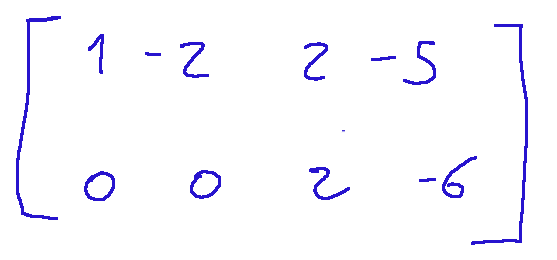
Step 2
Make the second pivot equal to 1
We divide the second row by 2 to get a pivot of 1 in (2,3), that is, we make R2 = R2/2
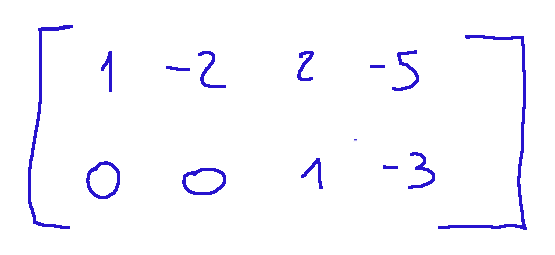
Step 3
Delete the element above the second pivot. To eliminate the 2 in position (1,3), we do the operation R1=R1-2R2
We will have the following matrix:
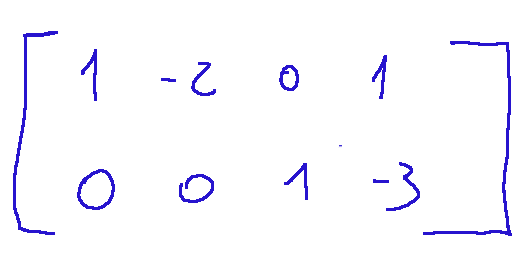
Result
Since there are no other steps to perform, we have reached the end of our elimination and the result of the simplified matrix is the next
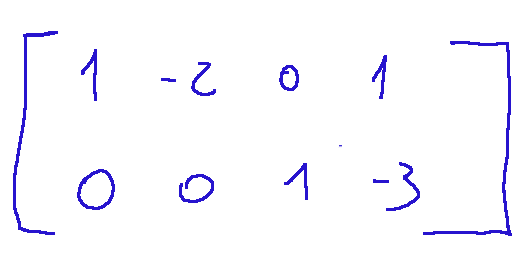
Considerations
In the Gaussian elimination method, the goal is to bring the matrix to the upper triangular form, that is, a matrix where all the elements under the main diagonal are equal to zero.
The Gauss-Jordan elimination method instead has the goal of bringing the matrix to the reduced Gaussian form (also called normal form), where in addition to being upper triangular, each pivot must be equal to 1 and the elements above and below each pivot must be 0.
Summary
Gauss: Only zeros under the main diagonal.
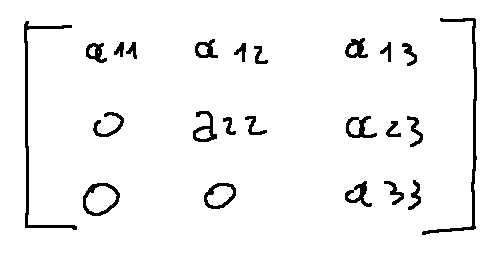
Gauss-Jordan: Zeros both above and below the main diagonal (longer and more complex operations).
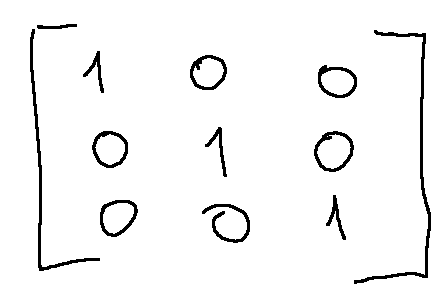
NOTE:
The pivot numbers of a matrix are the elements that are used to "drive" the elimination process in matrix reduction techniques, such as Gaussian elimination or Gauss-Jordan elimination.
NOTE II:
The Guss-Jordan elimination method is named after two great mathematicians.
Carl Friedrich Gauss (1777–1855), a German mathematician, who developed the Gaussian elimination method.
Thomas Hobson Jordan (1834–1891), an American mathematician who improved Gauss's method by developing the reduced form of the matrix, which is what we now call the "Gauss-Jordan method".
Conclusions
The main difference between the Gauss elimination method and the Gauss-Jordan method concerns the objective and the number of operations needed to reach the final form of the matrix.
Question
Have you heard of these two mathematicians, Carl Friedrich Gauss and Thomas Hobson Jordan?

[ITALIAN]
04-02-2025 - Geometria analitica - eliminazione di Gauss-Jordan [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_88)
***eliminazione di Gauss-Jordan ***
Questo metodo è una variante al metodo di eliminazione di Gauss
Procediamo con un esempio e prendiamo la seguente matrice:
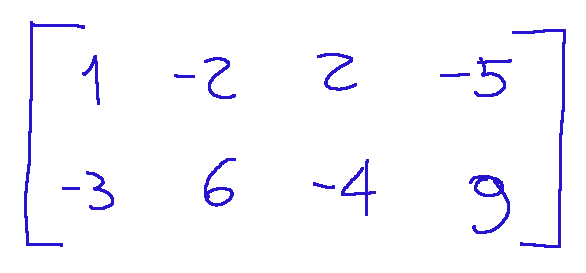
Applichiamo ora il metodo Gauss-Jordan
Passo 1
Eliminazione del primo elemento della seconda riga
Il primo pivot è già 1 in posizione (1,1), quindi usiamo la prima riga per eliminare il -3 in posizione (2,1) facendo R2=R2+3R1
otteremo la seguente semplificazione
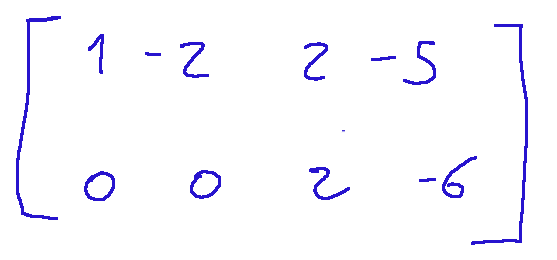
Passo 2
Rendere il secondo pivot uguale a 1
Dividiamo la seconda riga per 2 per ottenere un pivot 1 in (2,3), cioè facciamo R2 = R2/2
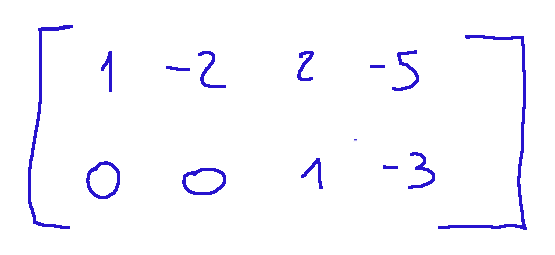
Passo 3
Eliminazione dell'elemento sopra il secondo pivot. Per eliminare il 2 in posizione (1,3), facciamo l'operazione R1=R1-2R2
Avremo la seguente matrice:
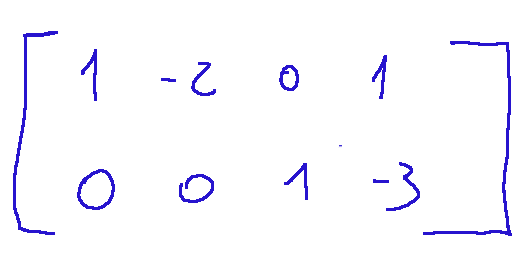
Risultato
Non essendoci altri passaggi da effettuare siamo arrivati in fondo alla nostra eliminazione ed il risultato della matrice semplificata è il seguente
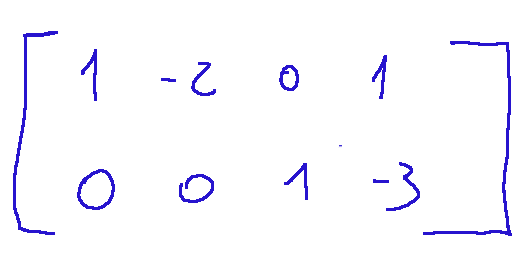
Considerazioni
Nel metodo di eliminazione di Gauss l'obiettivo è quello di portare la matrice alla forma triangolare superiore, cioè una matrice dove tutti gli elementi sotto la diagonale principale sono uguali a zero.
Il metodo di eliminazione Gauss-Jordan ha invece l'obiettivo di portare la matrice alla forma ridotta di Gauss (detta anche forma normale), dove oltre a essere triangolare superiore, ogni pivot deve essere uguale a 1 e gli elementi sopra e sotto ogni pivot devono essere 0.
Sintesi
Gauss: Solo zeri sotto la diagonale principale.
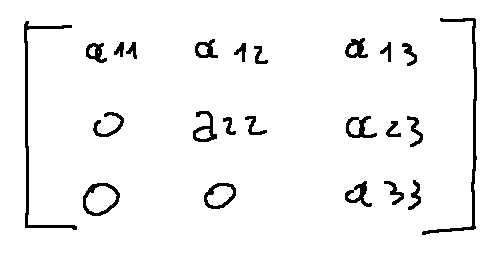
Gauss-Jordan: Zeri sia sopra che sotto la diagonale principale (operazioni più lunghe e complesse).
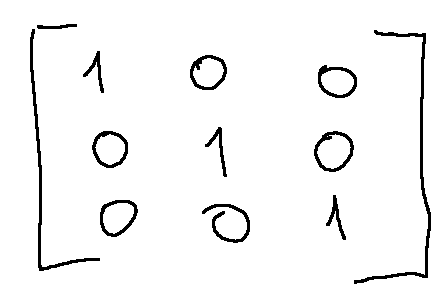
NOTA:
I numeri pivot di una matrice sono gli elementi che vengono utilizzati per "guidare" il processo di eliminazione nelle tecniche di riduzione delle matrici, come l'eliminazione di Gauss o di Gauss-Jordan.
NOTA II:
Il metodo di eliminazione Guss-Jordan prende il nome da due grandi matematici.
Carl Friedrich Gauss (1777–1855), un matematico tedesco, che ha sviluppato il metodo di eliminazione di Gauss.
Thomas Hobson Jordan (1834–1891), un matematico statunitense che perfezionò il metodo di Gauss sviluppando la forma ridotta della matrice, che è ciò che oggi chiamiamo "metodo di Gauss-Jordan".
Conclusioni
La differenza principale tra il metodo di eliminazione di Gauss e il metodo di Gauss-Jordan riguarda l'obiettivo e il numero di operazioni necessarie per raggiungere la forma finale della matrice.
Domanda
Avevate già sentito parlare di questi due matematici, cioè di Carl Friedrich Gauss e di Thomas Hobson Jordan?
THE END
Sorry to ask. Are you a lecturer?
And how did you learn all of these?
Thanks for stopping by. I am not a teacher. I like education of various kinds. I don't know many subjects well, actually I know many, but in a superficial way
I have so much admiration for Carl Fredrick Gauss who's called the Prince of mathematics. He produced a lot of mathematical ideas that are still useful to the field even today. This one you've presented today is fun and interesting. Have a good day.
He was an exceptional mathematician
This is similar to matrix or should I say it is a subtopics under matrix right. Thank you for sharing this with us also
We are still in the field of the study of matrices. Gauss-Jordan elimination is a method used to solve systems of linear equations and to calculate the inverse of a matrix. It is an extension of Gaussian elimination, in which the reduction process is continued until the canonical form of the matrix is obtained. !DHEDGE