
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH
18-11-2024 - Analytic Geometry - Cramer's Rule [EN]-[IT]
With this post I would like to give a brief instruction about the topic mentioned in the subject
(code notes: X_74)
Cramer's Rule
Description
Cramer's rule is a method for calculating the solution of a compatible system
with an equal number of linear equations and unknowns.
We can also give the following definition. Cramer's rule is a method used to solve systems of square linear equations, that is, with the same number of equations and unknowns, using the calculation of the determinants.
Definition
Given a system of linear equations of n equations with n unknowns:
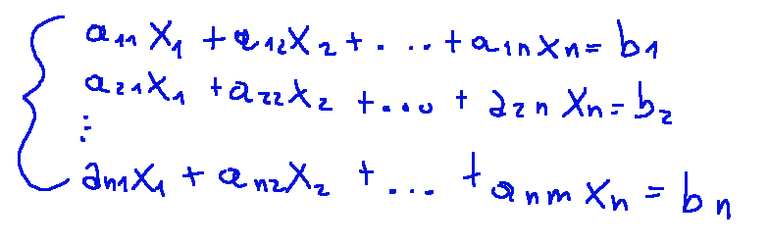
In matrix form we can write like this…
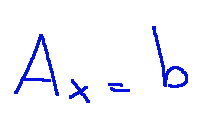
Where:
A is the matrix of coefficients (n x n)
x is the value of the unknowns (x1,x2,...,xn)
b is the vector of the known terms (b1, b2,..., bn)
Cramer's rule provides the solution by calculating it in the following way
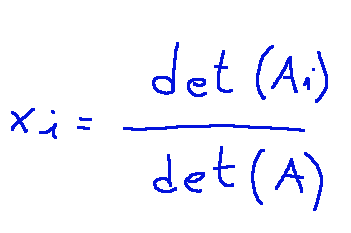
However, this is valid for every i=1, 2, …, n if and only if the det(A) is different from zero, that is, if A is invertible
The method
-Calculate the determinant of A
-Build the matrices Ai: Ai is the matrix obtained by replacing the i-th column of the matrix A with the vector b.
-Calculation of the determinants of Ai
-Calculation of the solution: Each unknown xi is obtained by dividing the determinant of Ai by that of A
Example
Let's consider the system proposed below
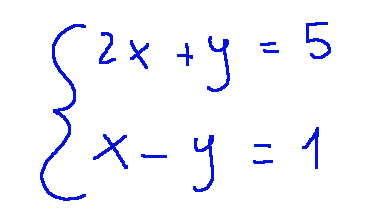
The coefficient matrix is so…
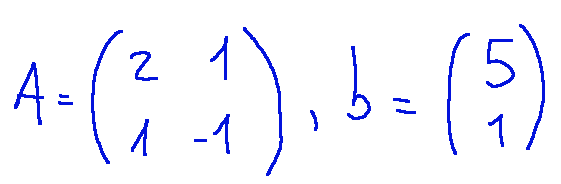
Now let's calculate the Determinant of A
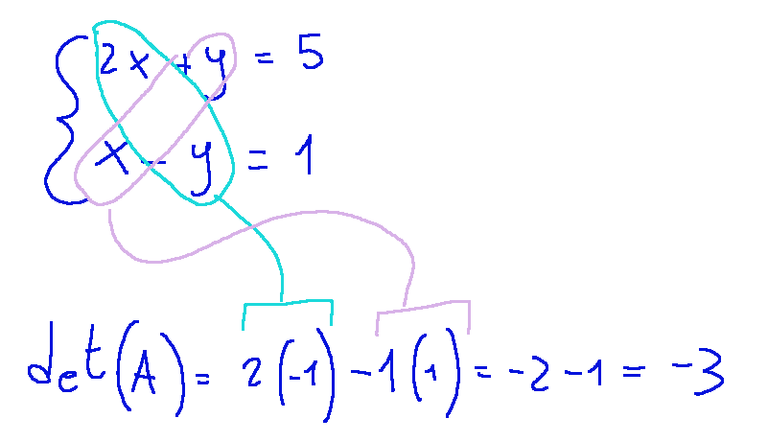
Now let's construct the matrices A1 and A2
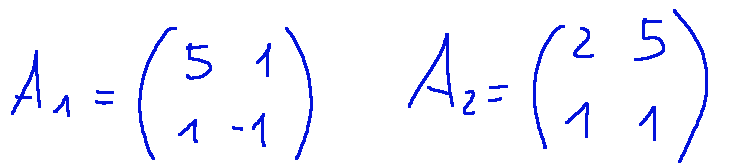
Now let's calculate the determinants of A1 and A2
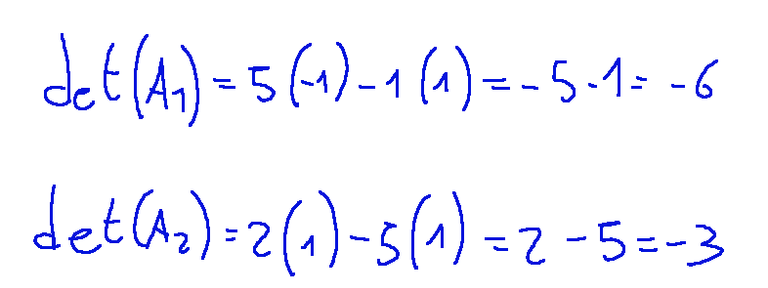
The solution x1 and x2 will therefore be the next
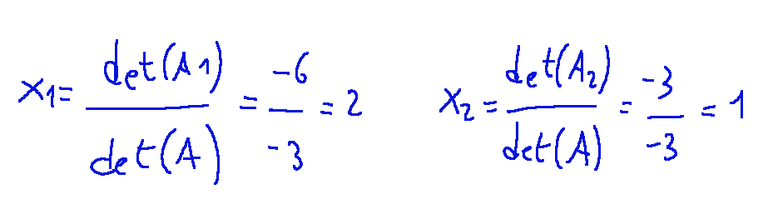
Conclusions
To solve systems of square linear equations, Cramer's rule can be used, but it is practical for small systems.
Question
Have you ever heard of Cramer's rule?

[ITALIAN]
18-11-2024 - Geometria analitica - Regola di Cramer [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_74)
Regola di Cramer
Descrizione
La regola di Cramer è un metodo per calcolare la soluzione di un sistema compatibile
con un numero uguale di equazioni lineari e incognite.
Possiamo anche dare la seguente definizione. La regola di Cramer è un metodo utilizzato per risolvere sistemi di equazioni lineari quadrati, cioè con lo stesso numero di equazioni e incognite, utilizzando il calcolo dei determinanti.
Definizione
Dato un sistema di equazioni lineari di n equazioni con n incognite:
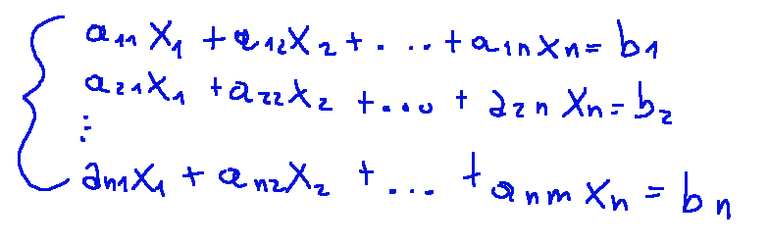
In forma matriciale possiamo scrivere così…
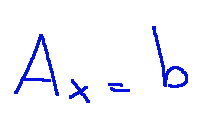
Dove:
A è la matrice dei coefficienti (n x n)
x è il valore delle incognite (x1,x2,...,xn)
b è il vettore dei termini noti (b1, b2,..., bn)
La regola di Cramer fornisce la soluzione calcolandola nella seguente maniera
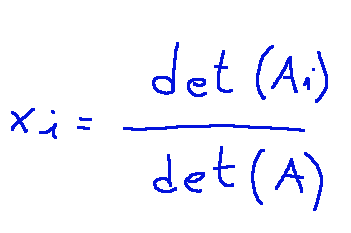
Questo però è valido per ogni i=1, 2, …, n se e solo se il det(A) è diverso da zero, cioè se A è invertibile
Il metodo
-Calcolare il determinante di A
-Costruire le matrici Ai: Ai è la matrice ottenuta sostituendo la i-esima colonna della matrice A con il vettore b.
-Calcolo dei determinanti di Ai
-Calcolo della soluzione: Ogni incognita xi è ottenuta dividendo il determinante di Ai per quello di A
Esempio
Consideriamo il sistema proposto qui sotto
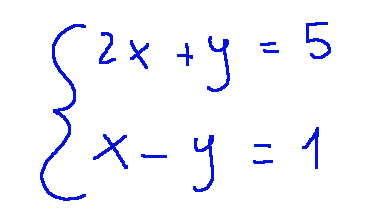
La matrice dei coefficienti è quindi…
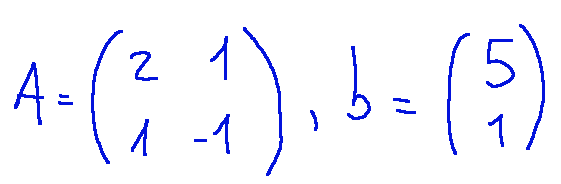
Calcoliamo ora il Determinante di A
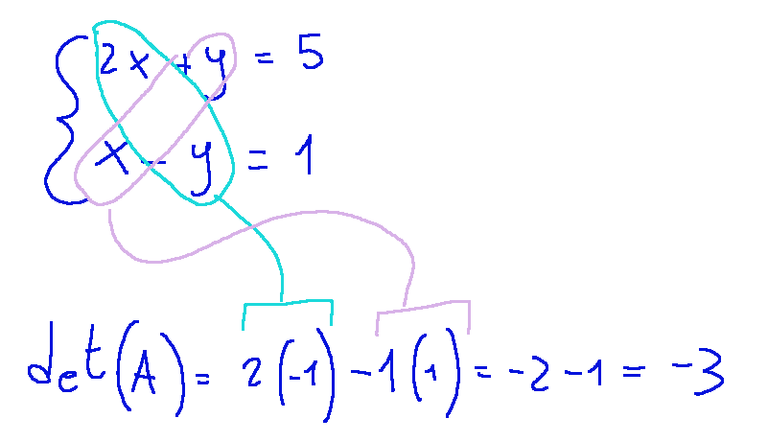
Costruiamo ora le matrici A1 e A2
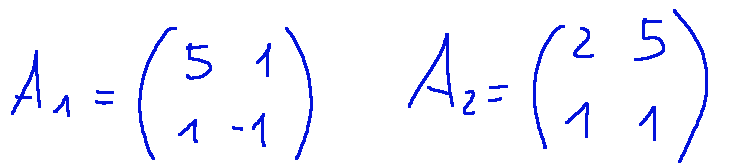
Calcoliamo ora i determinanti di A1 e A2
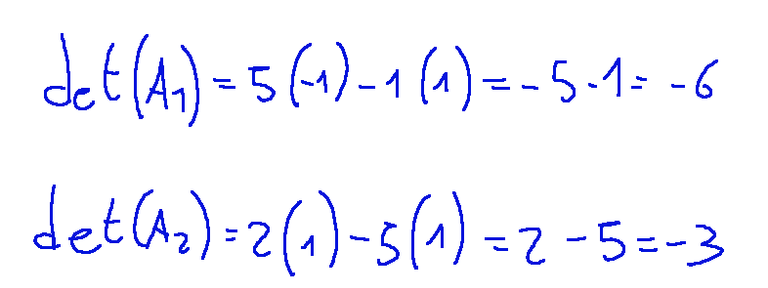
La soluzione x1 e x2 quindi sarà la seguente
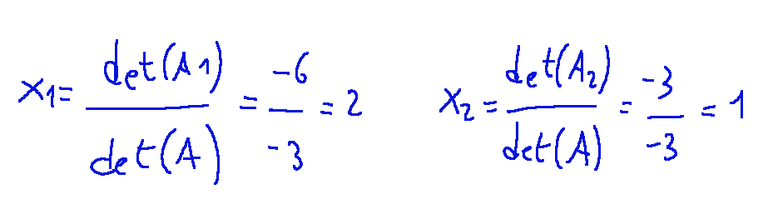
Conclusioni
Per risolvere sistemi di equazioni lineari quadrati si può usare la regola di Cramer, ma è pratica per sistemi piccoli.
Domanda
Avete mai sentito parlare della regola di Cramer?
THE END
!HOPE
!LOL
!INDEED
lolztoken.com
The Dim Reaper?
Credit: reddit
$LOLZ on behalf of cryptoyzzy
(8/10)
PLAY & EARN $DOOM
@stefano.massari, I sent you anYou took adequate time to explain this in a very detail way which I quite understand actually I must confess
If I hadn't dug out my old notes I would have had a hard time remembering everything.