
Mathematics are beautiful and they must be regarded as an art form in itself. From the beauty of symmetry, as admired by Leonardo da Vinci, to fractals and computer generated art in the modern times. Through the ages, man has always been struck by the elegance, the simplicity and truthfulness of mathematics.
Bertrand Russell expressed his sense of mathematical beauty in these words:
Mathematics, rightly viewed, possesses not only truth, but supreme beauty—a beauty cold and austere, like that of sculpture, without appeal to any part of our weaker nature, without the gorgeous trappings of painting or music, yet sublimely pure, and capable of a stern perfection such as only the greatest art can show. The true spirit of delight, the exaltation, the sense of being more than Man, which is the touchstone of the highest excellence, is to be found in mathematics as surely as poetry.
source: "A History of Western Philosophy".
As a young boy, in high school math class, I myself was struck by the beauty of the mathematical graphs. The sheer perfection of a parabola and a sine function has always stayed with me. Later in university, when I came to understand mathematics and its fundamental meaning much better, that admiration only grew.
After learning about Fourier transforms, it was a mind-blowing experience to actually see that everything - the world, the universe - can be considered as an interplay of waves - sine waves.
Inspiration
The inspiration for the collection that I have named MathArt comes from this fascination for math graphs, combined with my love for colors.
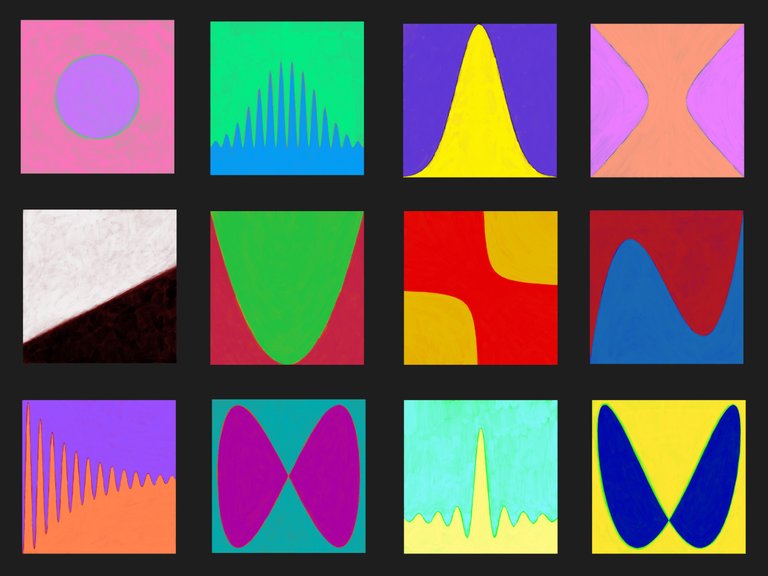
The series stems from analysis, the branch of mathematics that focuses on functions and equations. Each artwork is based on a striking member of a function family. Such as the polynomials, exponential and trigonometric functions, Lamé ellipsoids, cardioids (heart-shaped), folia (leaf-shaped), polynomials and Lissajous figures.
Elegant and harmonious lines in a basic square frame. Performed in sizzling colors, contrasting and interrelated in the graph of the function.
Even for those uninitiated to Mathematics, it's easy to recognize their beauty. For people who are mathematically literate, they open a new dimension to their stunning elegance.
Painterly Series I
This is the first series of twelve NFT's to be added to the collection.
"In der Beschränkung zeigt sich erst der Meister"
"Only in the limitation does the master show himself"
Source: Johann Wolfgang von Goethe, poem Natur und Kunst, 1800
The principle of the series is the beauty of simplicity. Just a simple square frame, a line and and two colored planes. No more.
Painterly Series color palette
All MathArtworks from the Painterly series consist of a selection of contrasting and very intense color combinations: two colors in the foreground and one color in the background. The background color plays an important role in the separation of surfaces and often shimmers through the foreground colors. This creates a very intense and vivid color experience for the viewer.
Two planes and a line
The line does not exist other than where two planes meet. Without those planes there is no line - and without that line there are no two planes. That dividing line, right there, that's where everything happens.
The formula
In addition, the formula of the graph depicted has been added to the NFT-card. Now you can actually own the formula and show it off to all your nerd friends.
How to collect MathArt?
MathArt was created on the Ethereum blockchain and can be collected from the creator bARTwerk or on the secondary NFT market. The collection of MarthArt by bARTwerk.eth was originally created on the Rarible-platform and is also available on Opensea.io. Any new owners can freely resell their MathArt NFT at their platform of choice.
Please make sure and check if the token you're buying is part of the original MathArt-collection: 0xf4d3d2b9d64e3d5cbd92038c808061dd08241615 on the Ethereum blockchain.
How many MathArt NFT are there?
The current (2022) number of minted NFT's is very limited (at the moment of publishing of this post only three works of these series have been published!).
The Painterly series I consists of only 12 artworks; the same as for series II.
How many there will be in the end I cannot tell you. But what I can tell you is that the total number of functions in mathematics is limited to let's say several dozens, and many of them will not make it as an NFT...
