Hello, Good day everyone!
The theory behind the way in which computers manipulate data is known as Boolean Logic. The fundamental building blocks of digital logic are the AND, OR, and NOT gates. Although circuits are implemented using other types of elements — particularly NAND gates. The logic design phase is most easily expressed in terms of the fundamental gates. The logic circuit symbols for AND, OR, NOT, and NAND are shown in the pictures below:
%20-%202022-03-23T074526.220.jpeg)
%20(14).png)
The Standard Boolean Operations
Boolean logic comprises a set of operations which manipulate logical, or boolean variables. A boolean variable can have either of two values known as true or false.
1) AND Gate
The output from an AND gate is 1 if all inputs are 1, otherwise it is 0.
%20-%202022-03-23T075909.619.jpeg)
Boolean expression: C = A.B
OR Gate
The Output from an OR gate is 1 if any of the inputs are 1, otherwise it is 0.
%20-%202022-03-23T080436.109.jpeg)
Boolean expression: C = A + B
NOT Gate
The NOT operation reverses the value of it's input.
%20(15).png)
Boolean expression: A = Ā
NAND Gate
The NAND operation is the same as an AND operation followed by a NOT operation. The output is 0 if all the inputs are 1, otherwise it is 1.
%20-%202022-03-23T081822.267.jpeg)
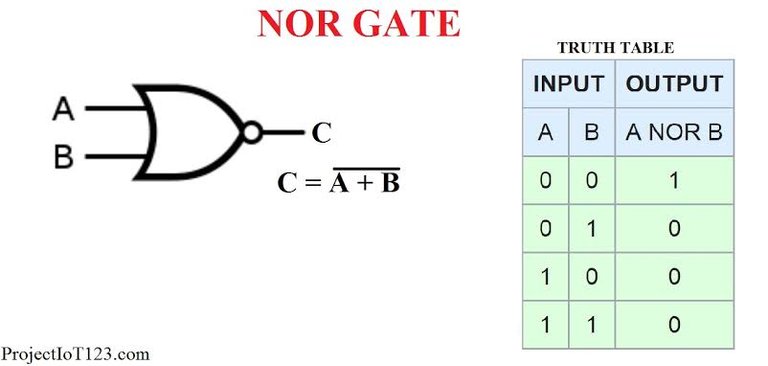
NOR Gate
The NOR operation is the same as an OR operation followed by a NOT operation. The Output is 0 if any of the inputs are 1, otherwise it is 1.
%20-%202022-03-23T083803.362.jpeg)
Rules for Boolean Logic
Boolean algebra, like any other algebra, consists of a set of elements, operators which act on the elements, and a number of rules which define the properties of both elements and operations.
A, B, and C are names of arbitrary elements of the set. In logic design, our interest is a Boolean algebra in which the set of elements contains only the identity elements namely {0,1}.
Rules of Boolean Logic
%20(16).png)
Two theorems in particular are very important: (A.B)' = A' + B' and (A + B)' — the so called de Morgan's laws named after their originator. These tell us how the inverse of arbitrary logic expressions can be rewritten in terms of the inverted variables in the expression.
According to the table above, associative law describes the properties of '.' and '+' which are very similar to the properties of the arithmetic operators in everyday algebra of real numbers.
Conclusion
Boolean Logic is a very important concept in computer manufacturing! These logics can also be used to build memory for storage of data. It can be used to build half adders and full adders. Thanks so much for reading my content, I appreciate you alot! Please don't forget to drop your comments in the comment sections below! Bye for now 👋 and I will see you in my next post!
[source](https://steemit.com/hive-138458/@anyiglobal/zero-to-infinity-education-or-information-logic-gates-and-circuits-by-anyiglobal)
Yay! 🤗
Your content has been boosted with Ecency Points
Use Ecency daily to boost your growth on platform!
Support Ecency
Vote for new Proposal
Delegate HP and earn more, by @anyiglobal.