
Hello friends and followers of STEM content, in this post as usual I want to explain a topic of differential calculus, in this are the reasons why we can calculate the relative extrema of a function by means of the criterion of the second derivative.
Remembering a little, we have that with the criterion of the first derivative, we find the first derivative of the function and equal to zero, we find the critical numbers, which are the numbers whose interval generates the points where the function reaches its maximum point and / or its minimum point.
However it is not only by the criterion of the first derivative that we can get the relative extrema of a function, but also by the criterion of the second derivative, the reason why we can find the relative extrema of a function by means of the criterion of the second derivative is because of:
Theorem: Criterion of the second derivative for calculating relative extrema of a function
Let f be a function such that f'(c) =0 and whose second derivative exists on an open interval that contains c. It follows that:
- If f''(c)>0, then f(c) is a minimum point.
- If f''(c)<0, then f(c) is a maximum point.
- If f''(c) = 0, it implies that the criterion of the second derivative is inconclusive and that we must resort to the criterion of the first derivative.
The meaning of this theorem is that if we find the first derivative of a function and equal it to zero, then we can find the critical numbers, in case such critical numbers exist for the second derivative, then if the substitution of such critical numbers in the second derivative is greater than zero it is because such point is a minimum point, in case the substitution of the critical numbers in the second derivative is less than zero it is because such point is a maximum point, and if it is equal to zero, then we must resort to the criterion of the first derivative since it is inconclusive.
Example for calculating the relative extrema of a function by means of the second derivative criterion.
Find the relative extrema of f(x)=-3 x^(5)+5 x^(3).
To find the solution of this exercise, we apply the theorem of the second derivative criterion, in which the first step is to find the first derivative as follows:
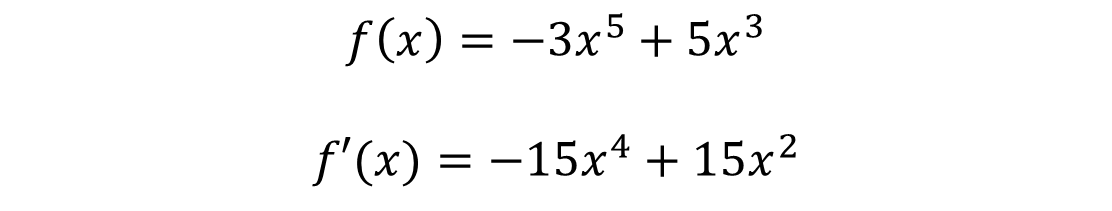
The second step is to equal the first derivative to zero and find the critical numbers:
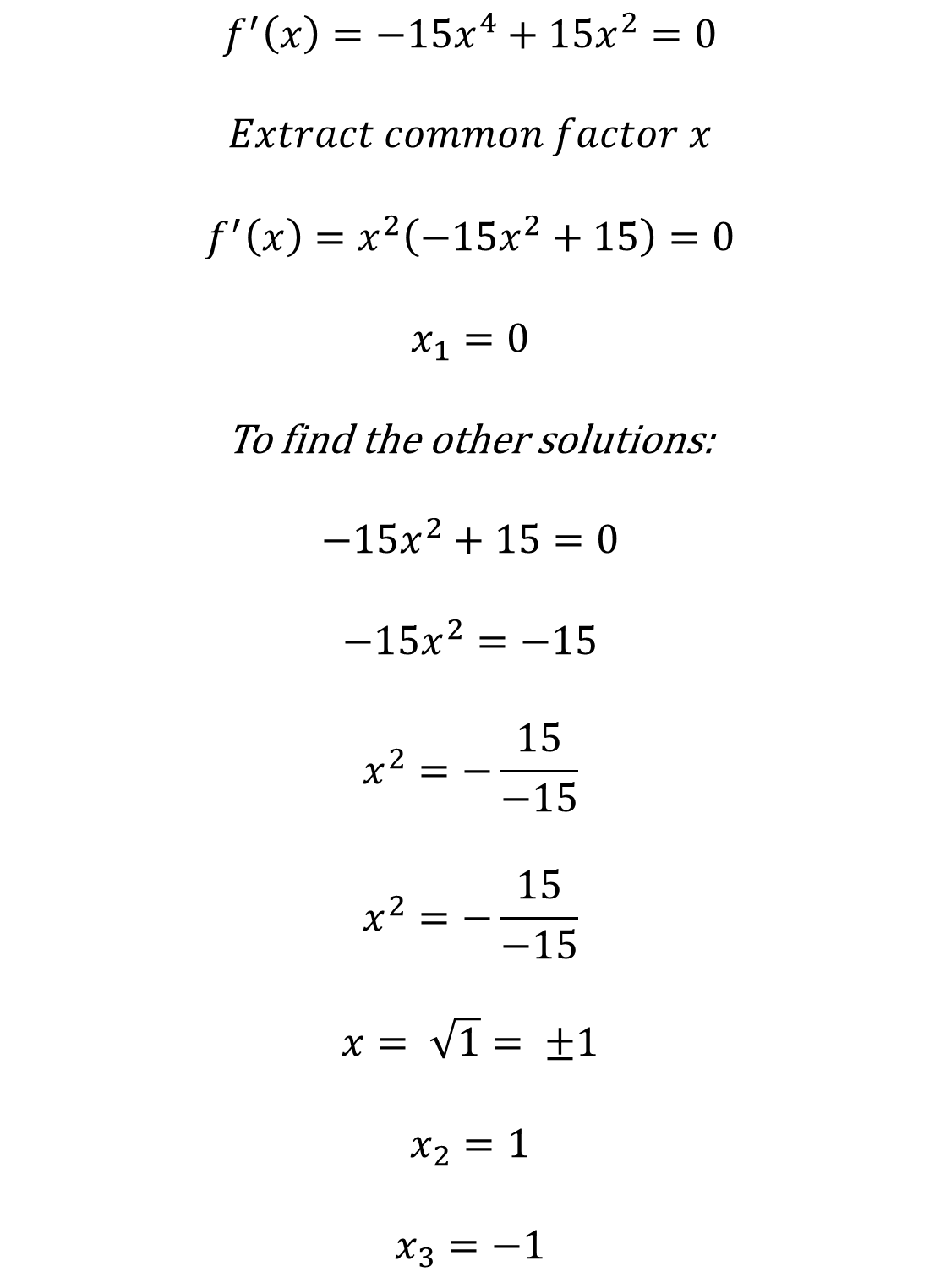
Tras obtener la primera derivada e igualar a cero, obtenemos que los números críticos son: X1 = 0 ; X2 = 1 ; X3 = -1
As a third step we find the second derivative as follows:
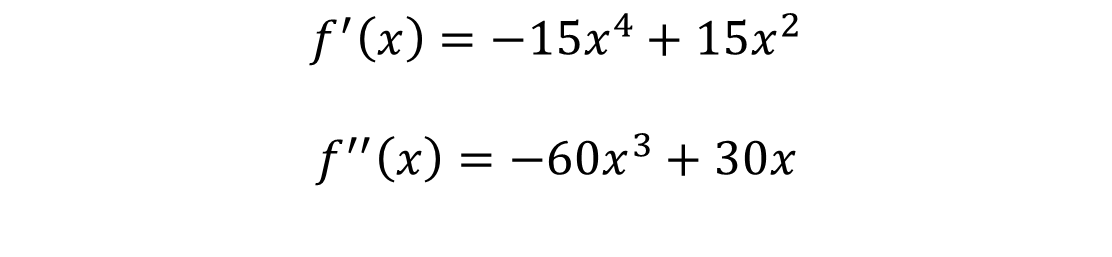
As a fourth step, we substitute the critical numbers in the second derivative:
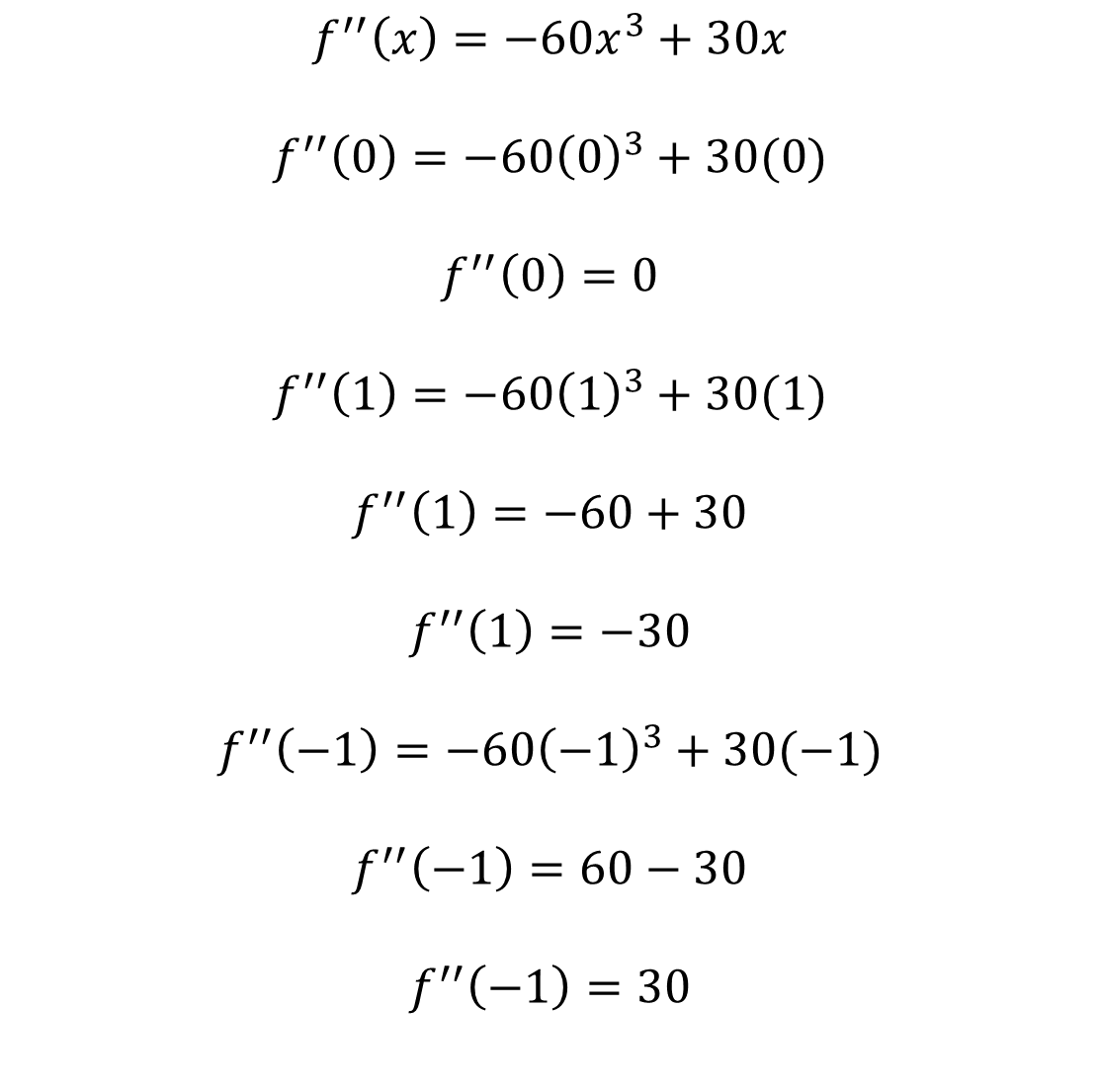
As a fifth step, we analyze the second derivative at the critical numbers of X = 0 ; X = 1 ; X = -1.
As f''(0) = 0 it is inconclusive.
As f''(1) =-30 and -30<0, it implies that it is a maximum point.
As f''(-1) = 30 and 30>0, it implies that it is a minimum point.
As a fifth step, we substitute X = 1 and X = -1 in the function f(x)=-3 x^(5)+5 x^(3), and thus find the y-coordinate of the maximum and minimum points of the function:

With this we conclude that the function has a maximum point at the point (1 ; 2) and has a minimum point at the point (-1 ; -2), as we can corroborate in the graph generated with the geogebra software:


Conclusion
The conclusion for this post is that the criterion of the second derivative is conclusive to find the relative maxima of a real function as long as the critical numbers found with the first derivative when substituted in the second derivative of non-zero, because if it gives us equal to zero is inconclusive and we have to resort to the criterion of the first derivative.
Recommended Bibliographic Reference.
Calculus with Analytic Geometry. Volume I. 7th edition. Author: Larson and Hostetler.
Note: All equations in this post were prepared using Microsoft PowerPoint equation insertion tools. The graph of the rational function was made using geogebra software.