What do we find when we derive a function f(x)?
According to the geometric interpretation of the derivative of a function f(x) is that when we derive a function and evaluate it at a point (x;y), what we are finding is the slope (m) of the line that is tangent to f(x) at that point (x;y).
Therefore if our objective is to be able to know the point or points where a function f(x) has horizontal tangent lines, it has to be where its derivative is zero, that is to say when we equal the derivative of a function f(x)=0 we are calculating the point or points where the tangent lines to f(x) are horizontal, since when a line is horizontal it is because its slope (m) = 0.
To prove this we are going to carry out the proposed exercises of the book of calculus with analytical geometry of Larson and Hostetler of the section 2.3 (page: 139) exactly the exercise 57 and 58 that say this way:
In the exercises 57 and 58, determine the point or points where the graph has horizontal tangent:

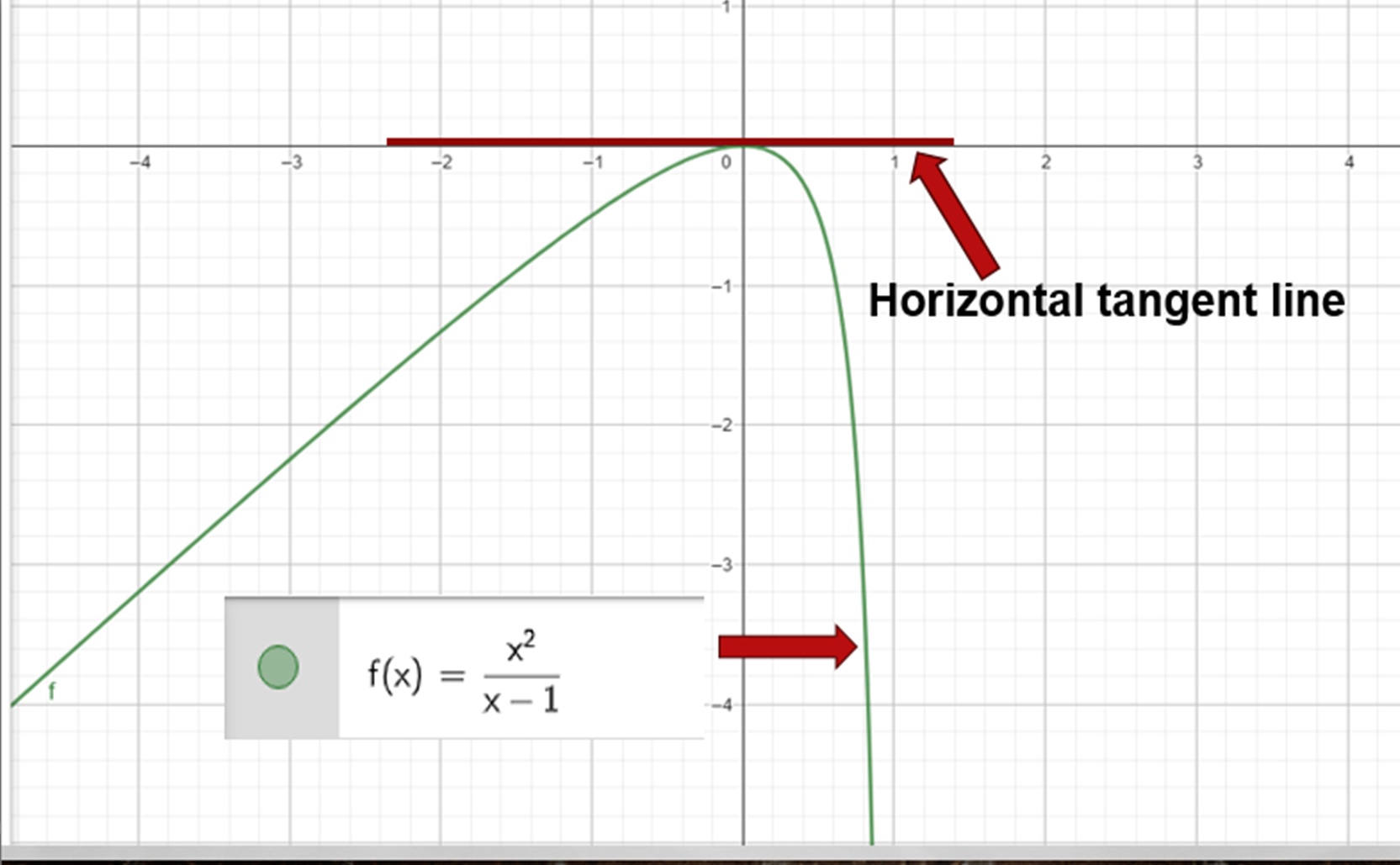
The first step we are going to take is to calculate the derivative of each of the two functions, and then we are going to take those derivatives and equal them to zero, i.e. f'(x) = 0.
The second step is to find the solution for the equations that we have left, for the values of X we substitute them in f(x) and find Y, so the points (X;Y) are the points where the tangent line is horizontal to f(x).
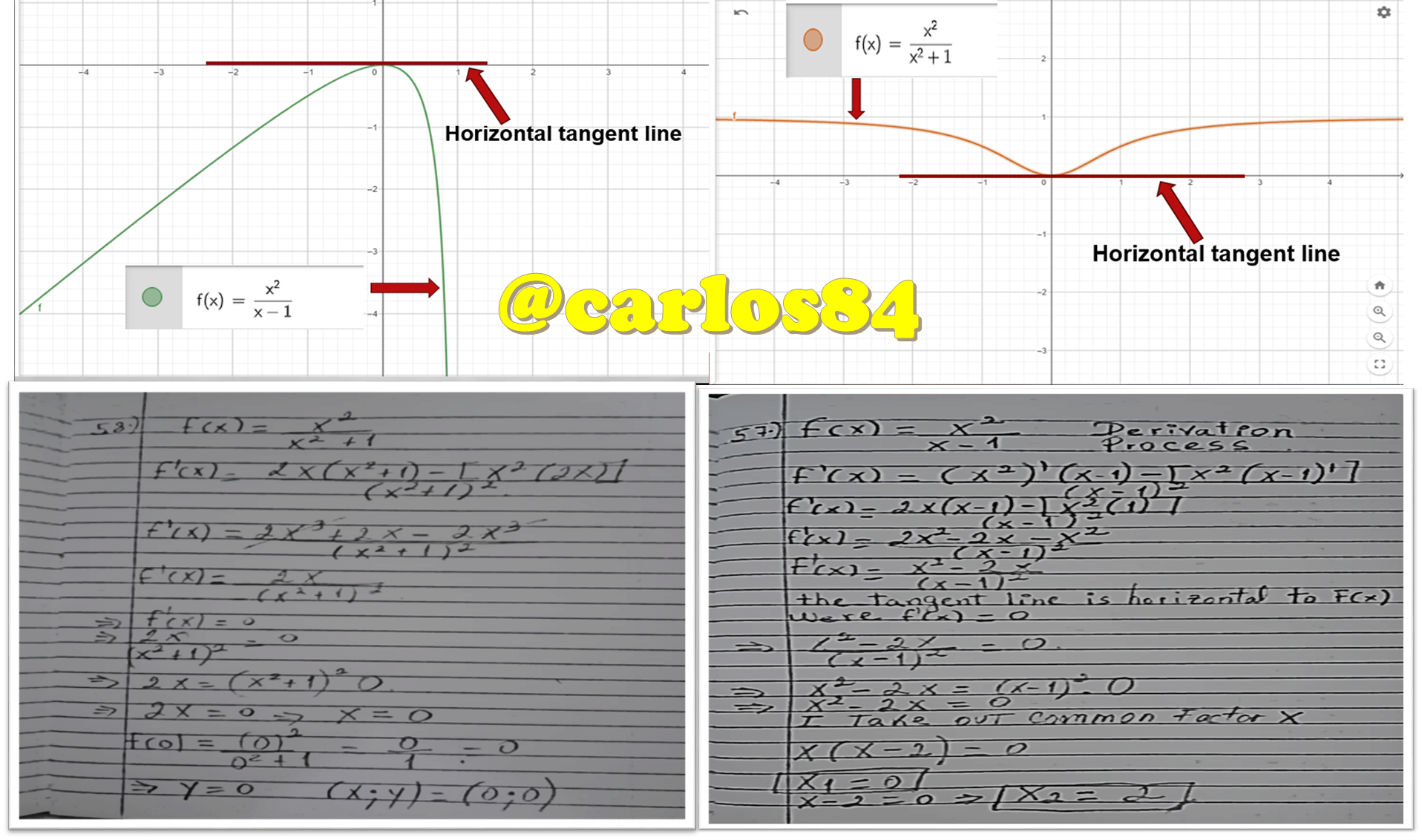
As a third step we are going to verify the veracity of the points found by graphing with the geogebra software.

Of the possible points where the derivative of f(x)=0 only the line passing through the point (0;0) is horizontal.
Let's see exercise 58:
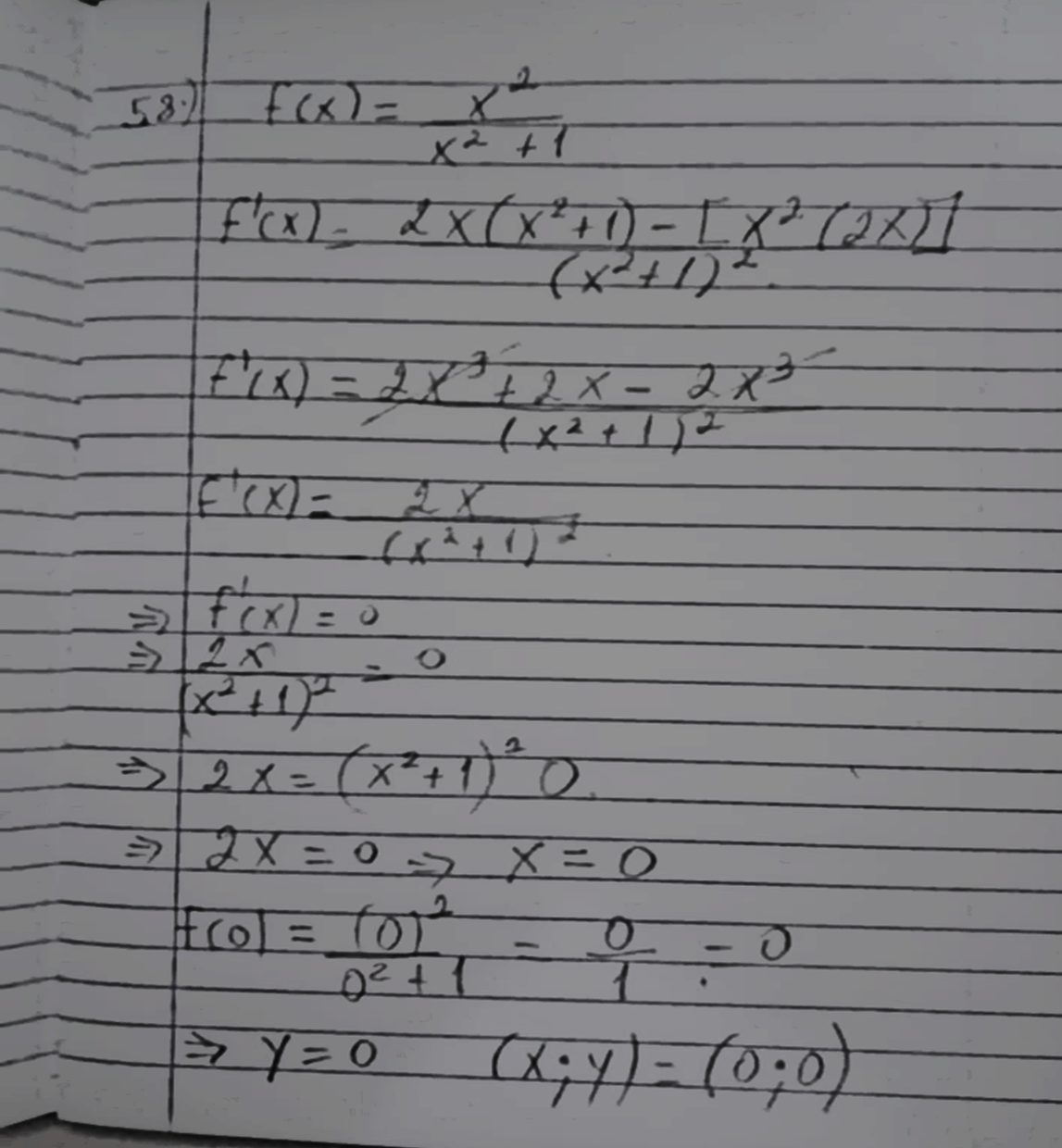
This means that the function f(x) of exercise 58 has only one point (0;0) where there is a horizontal line that is tangent, which we will corroborate with the geogebra graph:
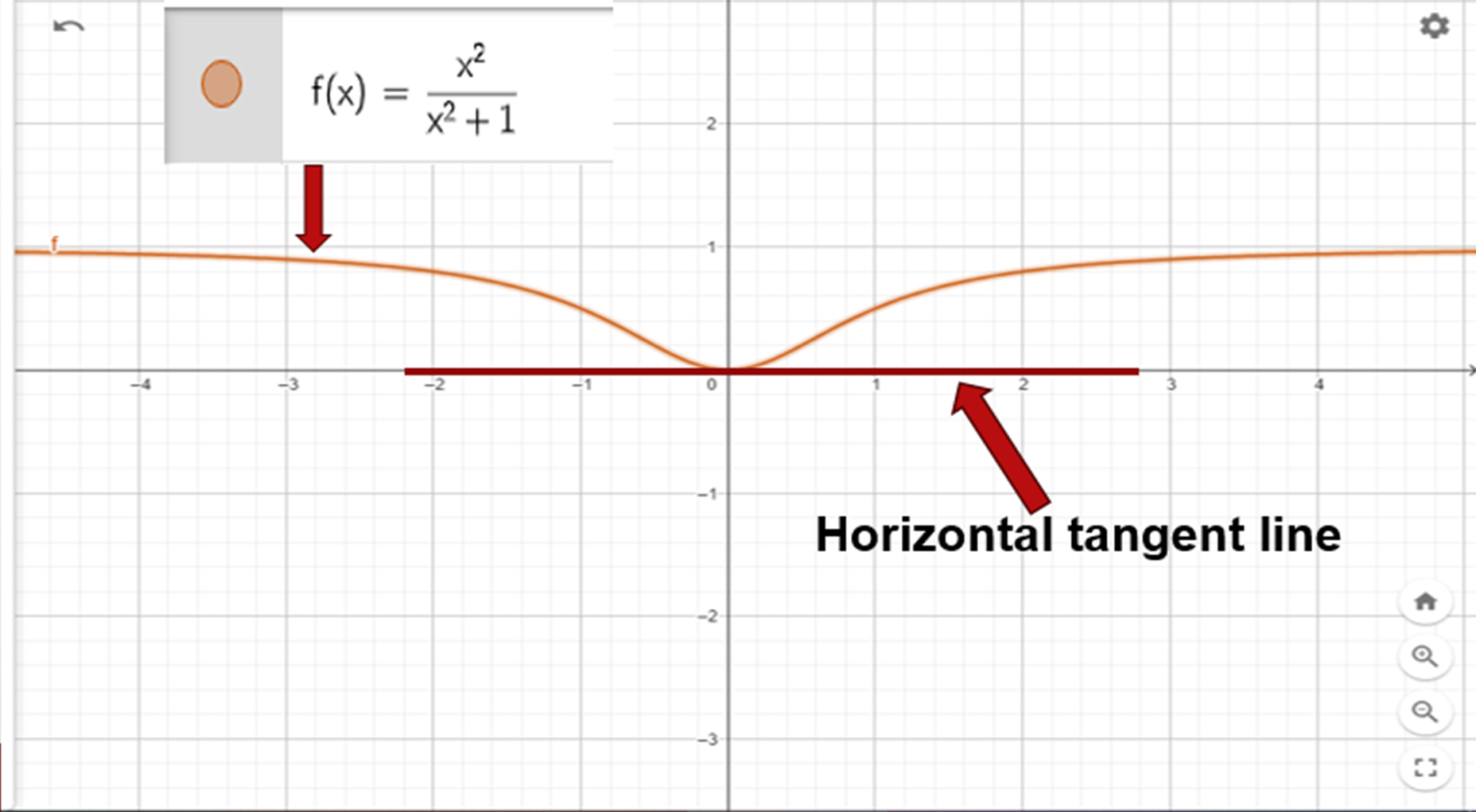
Conclusion
The conclusion is that whenever we want to get the tangent lines that are horizontal to f(x), simply find the derivative of f(x) and equal to zero: f'(x)=0.
There may exist one or several points through which pass horizontal tangent lines to f(x), in the case of the two exercises that were explained only have horizontal tangent lines at the point (0;0).
Recommended Bibliographic Reference
Calculus with Analytic Geometry. Volume I. 7th edition. Author: Larson and Hostetler.
Note: All equations in this post were prepared using Microsoft PowerPoint equation insertion tools. The graph of the rational function was made using geogebra software.