To get the equation of a line we only need to know the coordinates of two points that belong to the line, or at least know the coordinates of a point that belongs to the line and the slope of the line.
For this particular case what we have as data is a cubic function and the equation of a line that is parallel to the line that is tangent to the cubic function.
The solution is to find the derivative of the cubic function, then for a value of x= c we will find the coordinates of the point that is tangent to the cubic function at that point, therefore we say that for two lines to be parallel their slopes are equal, so m1 = m2.
From the line that is parallel to the given line, we would have as data the coordinates of a point and the slope, so we can apply the point-slope equation and find the equation of the line that is tangent to the cubic function.
Problem statement
Find the equation of the tangent line to the graph of f(x) = x3 + 2 and which is parallel to the line 3x-y-4 = 0
We find the derivative of f(x)
f'(x)= 3x2
What if x = 1?
Implies that f'(1) = 3(1)2
Implies that f'(1) = 3
From the line that is tangent to f(x) = x3 + 2 we know the point whose coordinate (x;y) = (1;3)
From the line that is tangent to f(x) = x3 + 2 we know the slope, since if two straight lines are parallel it is because their slopes are equal, therefore:
3x-y-4 = 0
3x-4 = y
The point-intercept equation of the line is: y = mx +b, where m is the slope and b is the intersection with the y-axis. Therefore:
m2 = 3, and since m1 = m2, then m1 = 3.
What do we have now of the line that is tangent to f(x) = x3 + 2?
The data we have are the coordinates (x,y) of the point = (1,3) and m = 3
What do we apply to find the equation of the line if we know a point on the line and its slope?
We apply the equation point - slope of a straight line:
y-y1 = m (x-x1)
y-3 = 3 (x-1)
y-3 = 3x-3
y = 3x-3 +3
y = 3x
Conclusion and analysis of results
To check that the line y = 3x really is tangent to f(x) = x3 + 2 and is parallel to the line y = 3x-4 we simply plot with GeoGebra software:
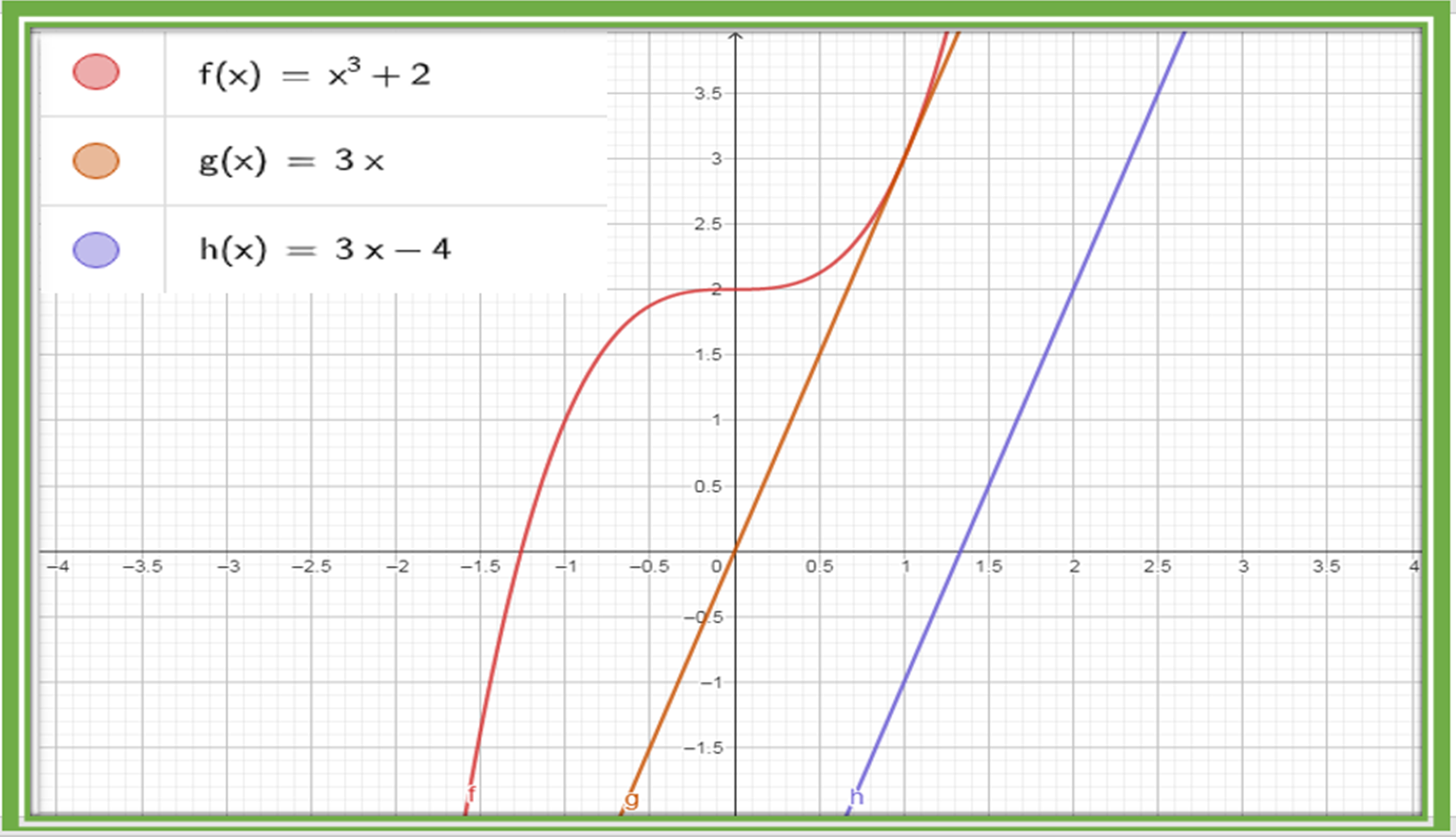
Podemos observar claramente como la recta g(x) = 3x es tangente a f(x) = x3 + 2 en el punto cuya coordenada (x,y) es (1,3) y a su vez es paralela a la recta h(x)= 3x-4, por lo que nuestros cálculos son correctos encontrando la ecuación de la recta que es tangente a f(x) = x3 + 2 y paralela a la recta h(x)= 3x-4
Bibliography consulted and recommended
Calculus with Analytic Geometry by Larson and Hostetler. Volume I. 8th edition.



@tipu curate