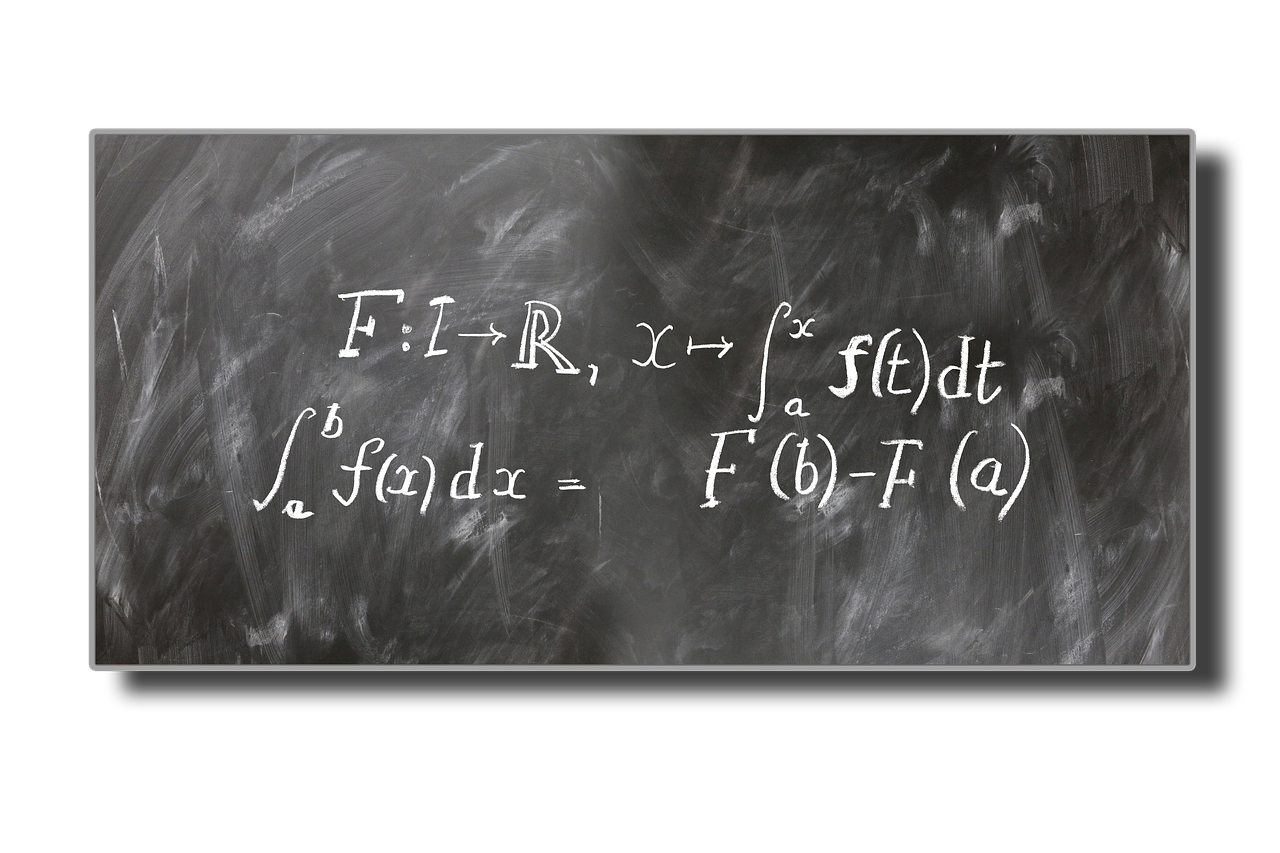
Image source
The method of disks is extended to solve the calculation of the volume of a solid in revolution that is hollow, for this the method of disks replaces the disk by a washer or ring.
How is the washer or ring formed?
The washer is formed by rotating a rectangle around an axis as shown:
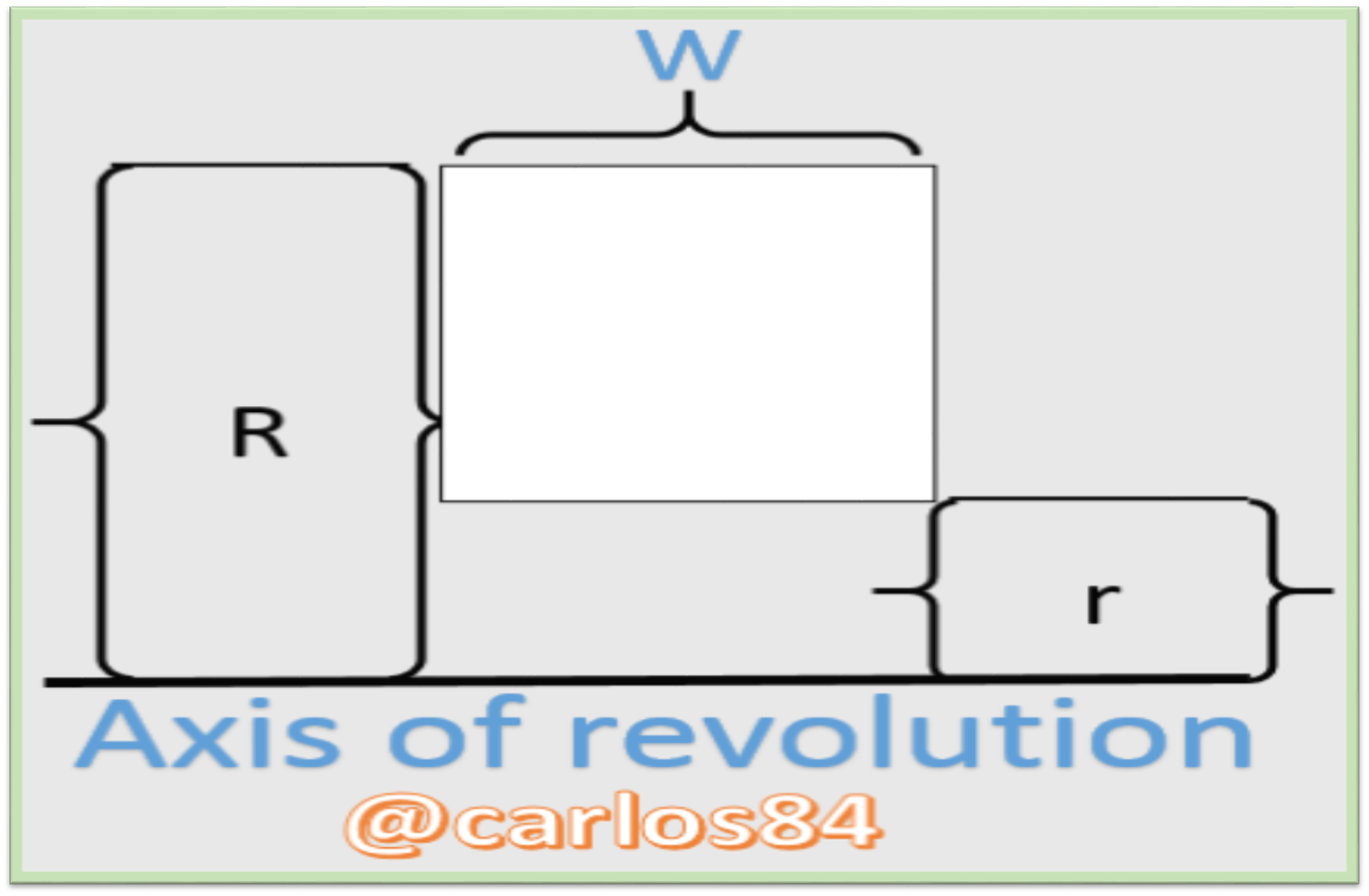
The volume of a washer or ring is equal to 𝜋 times the difference of the radii times W, i.e:
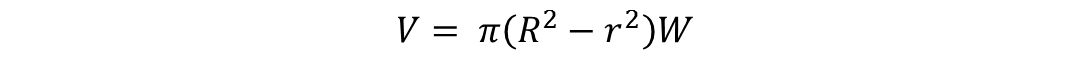
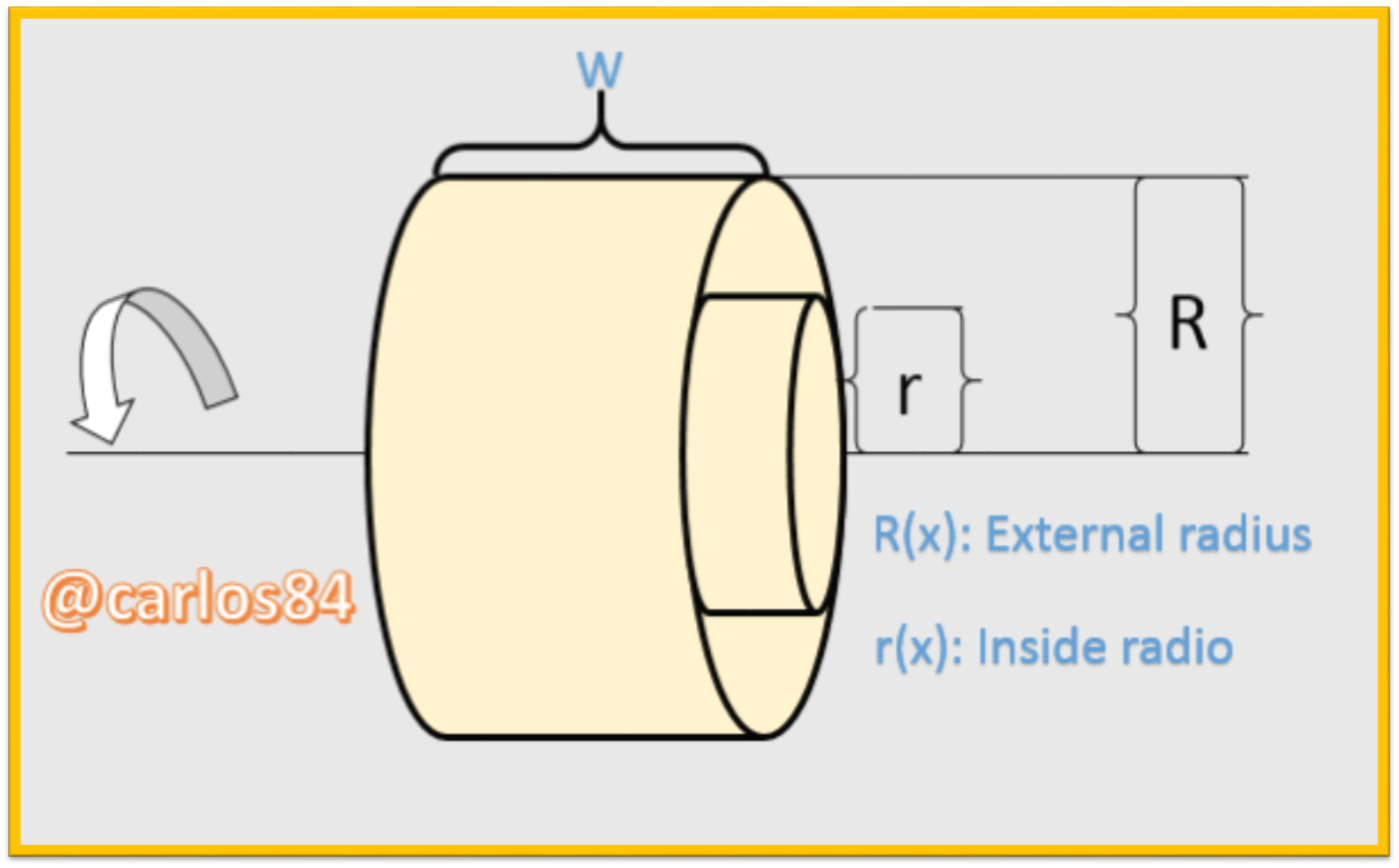
In order to understand how the integral can be used in the calculation of the volume of a solid in revolution by the method of washers or rings, we must consider a region of the plane (x,y) that is bounded by an outer radius R(x) and an inner radius r(x), so that if the region is rotated around its axis of revolution, the figure is as follows:
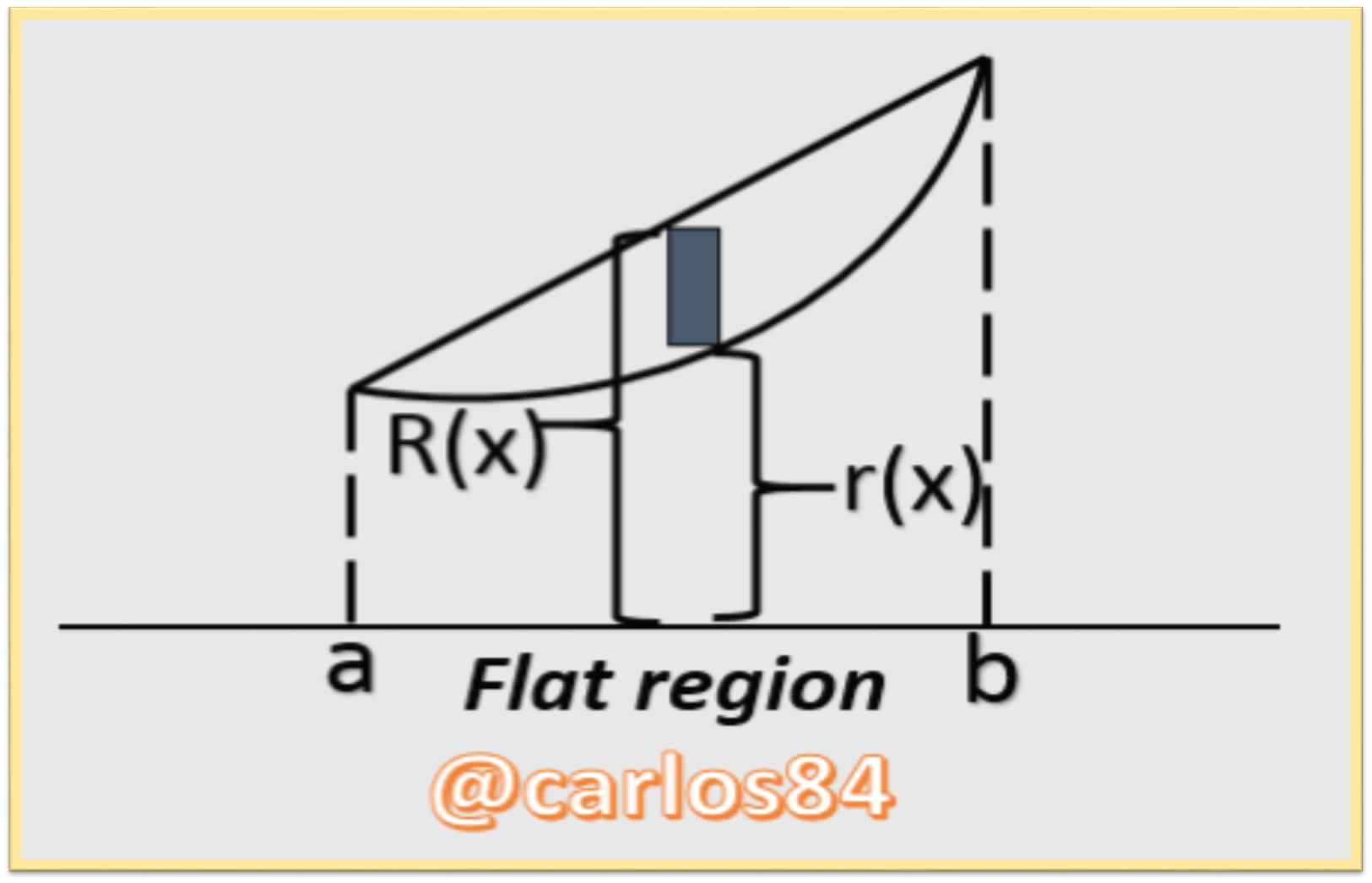
Therefore, the volume of the resulting solid when the plane region is rotated is:
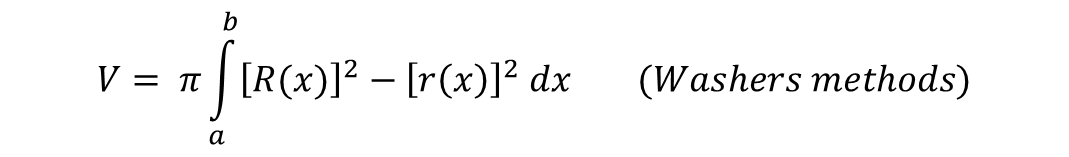
Use of the washer or ring method for calculating the volume of a solid in revolution
Find the volume of the solid formed by rotating the region bounded by the graphs of:
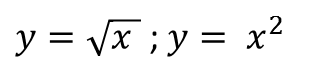
around the x-axis, as shown in the figure below:
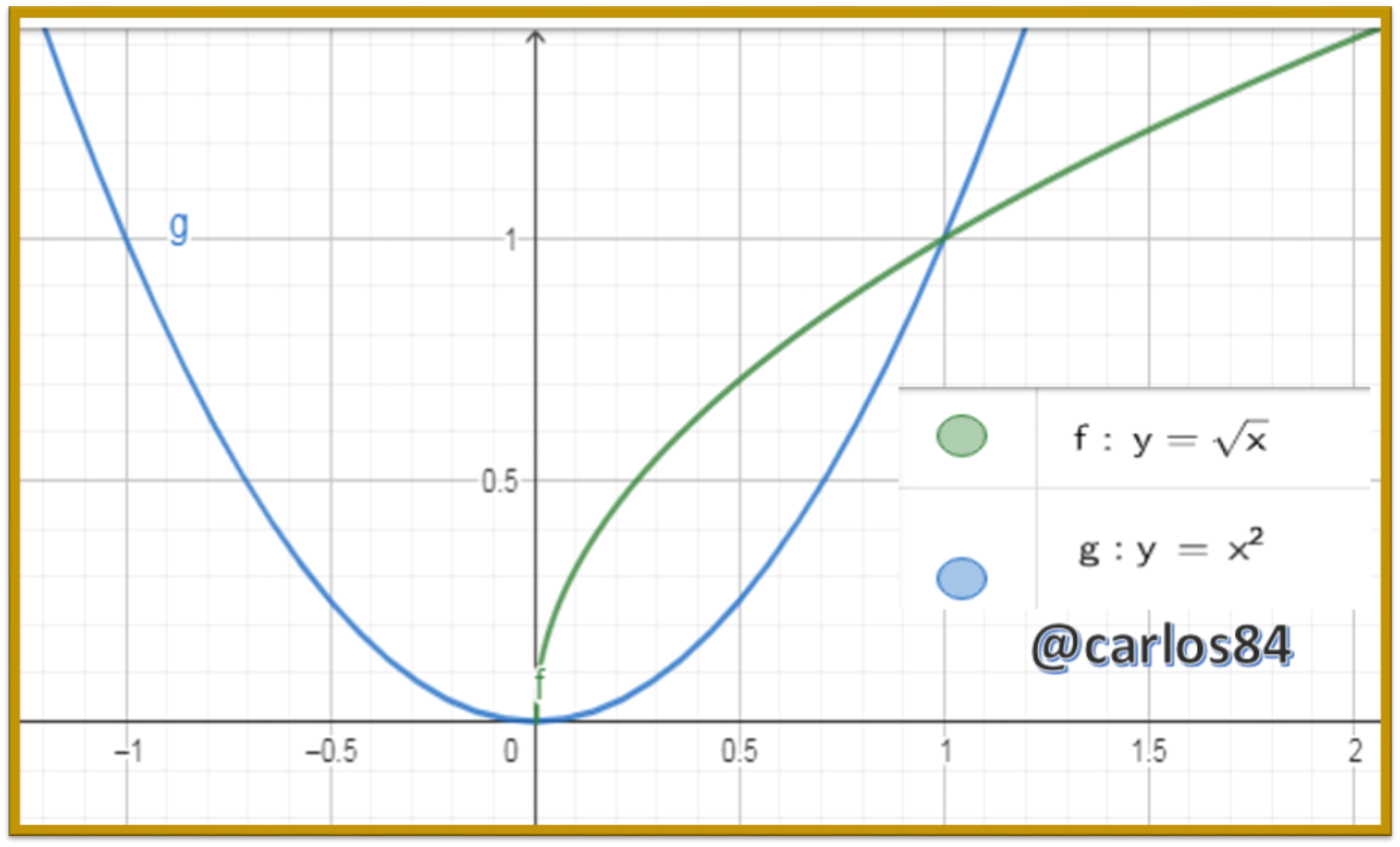
The two curves intersect at x= 0 and x = 1, so the region of the plane that will be taken into account to rotate around the x-axis is:
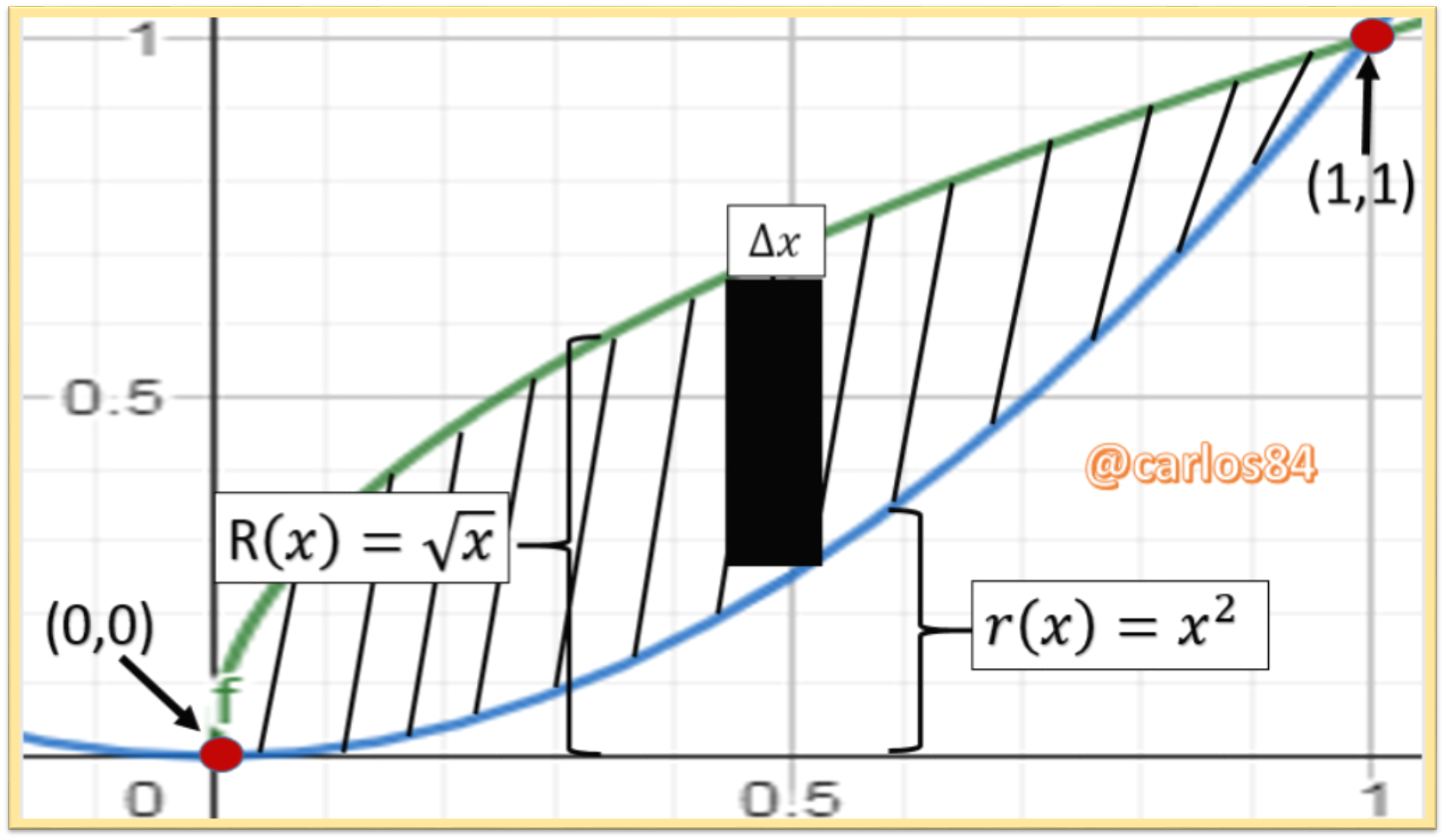
So the approach to solve the volume is:
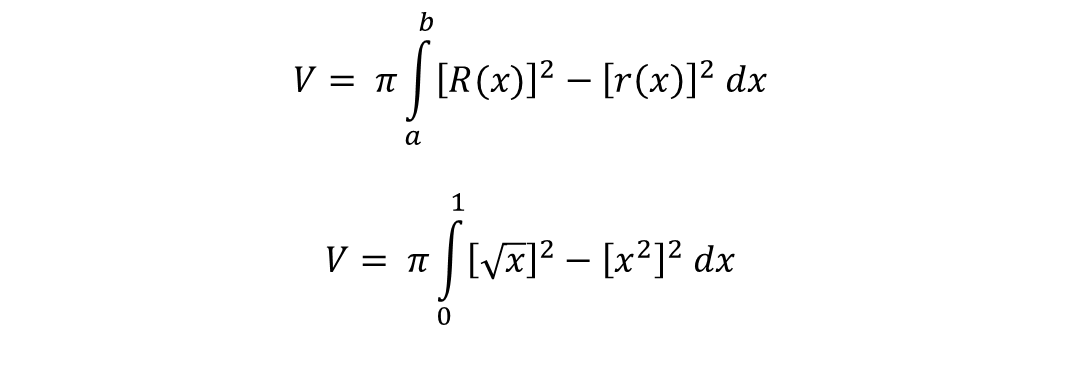
Solving the integral we are left with:

Consulted and recommended biography
Book of calculus with analytic geometry by Larson and Hostetler. Volume I. 8th edition.
Note: The equations used in this publication were elaborated using the equation insertion tools of Microsoft PowerPoint. The images without fonts were elaborated using Geogebra software and Microsoft PowerPoint.