Hello friends and followers of STEM content, this time I want to explain an exercise of infinite limits, with which we will learn if when a function approaches a number (a) and f(x) results in infinity, it can happen that in (a) there is a vertical asymptote, and if the limit can be solved to end the indeterminacy, it implies that it is a false vertical asymptote, and that the reality is that it is an infinite limit but with a discontinuity in X=a but it is a discontinuity of the inevitable type.
For this we will pose the following question:
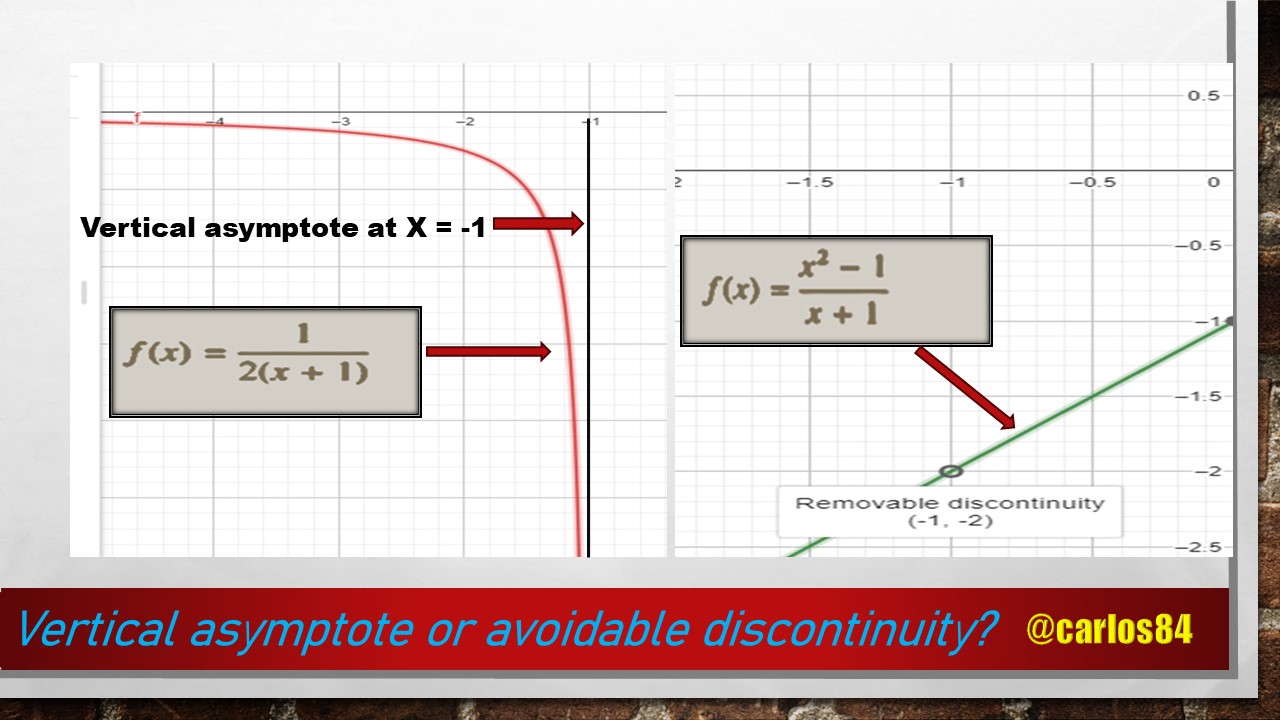
Determine whether the following functions have a vertical asymptote or an avoidable discontinuity:
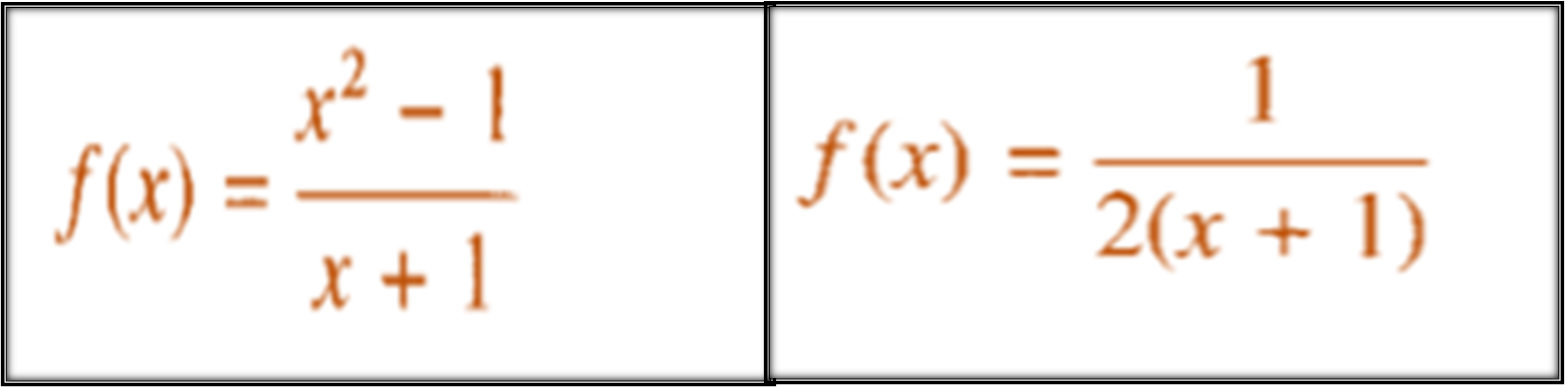
The first conceptual thing to know is that a rational function such as those shown above, have a vertical asymptote for a specific value of X where the denominator cancels out, however it may not necessarily be a vertical asymptote, because if we then solve the limit of the function for when x tends to the value where the denominator cancels out, and the limit exists, then it was a false vertical asymptote, and we can verify this graphically using the geogebra software.
Let's start by analyzing the following function:
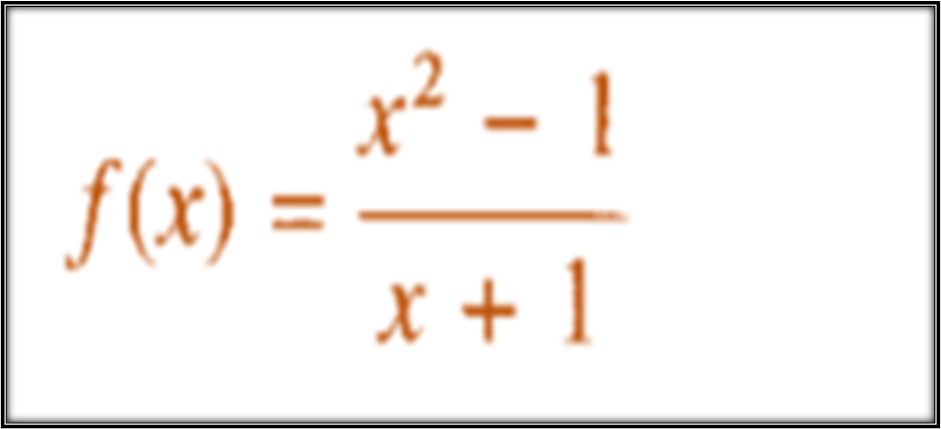
As can be observed the denominator of the rational function shown above cancels out when X = -1, therefore let is likely that there is a vertical asymptote at X = -1, however if we solve the limit of f(x) for when X tends to -1 and gives us a real value, it means that it does not have a vertical asymptote at X = -1, but it is an unavoidable discontinuous function at X = -1.
The limit I propose to solve for is:

If we perform the direct substitution of the limit when X tends to -1 we will realize that it will give us a result that is an indeterminacy of the form 0/0:
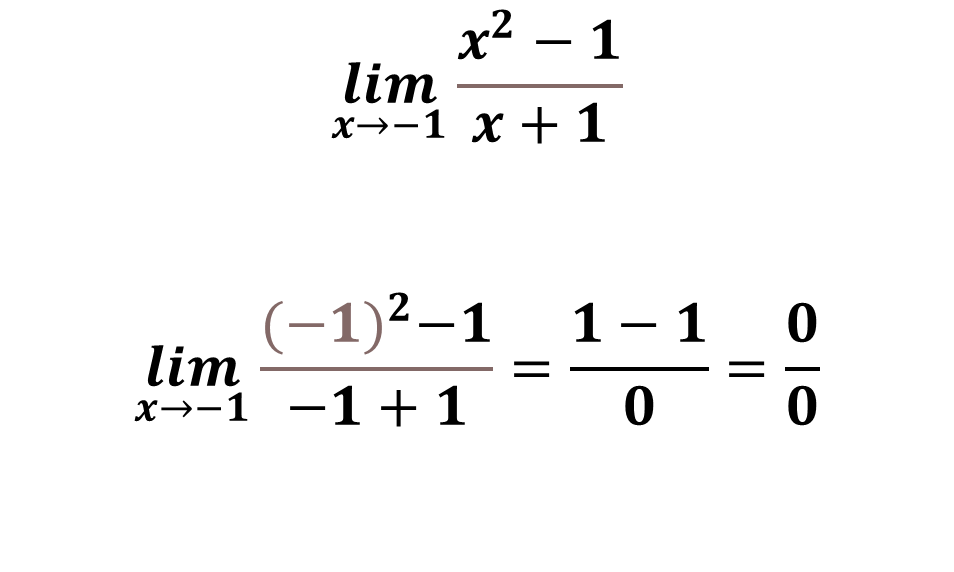
This means that having the denominator annulled, we would think that there is a vertical asymptote at X = -1, however if we look at the numerator of the rational function we can realize that it can be factorized
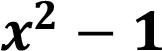
The factorization of this second degree binomial is:
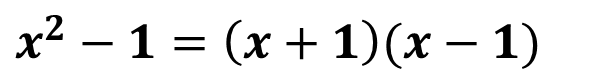
El límite nos quedaría planteado de la siguiente forma:
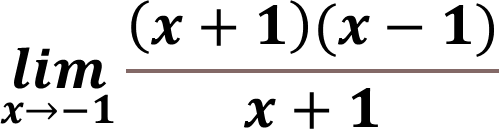
We can see that there are two equal terms in both the numerator and the denominator which is (x+1) which cancel each other out:
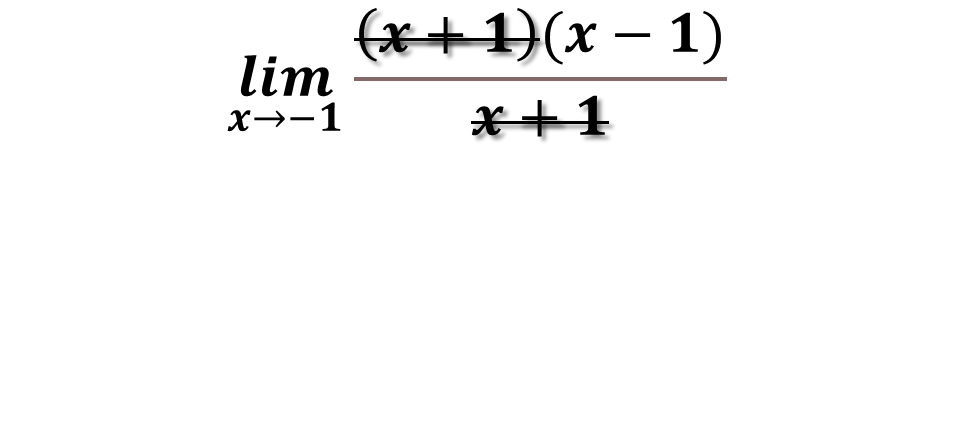
This implies that after simplifying we have to solve the following limit:
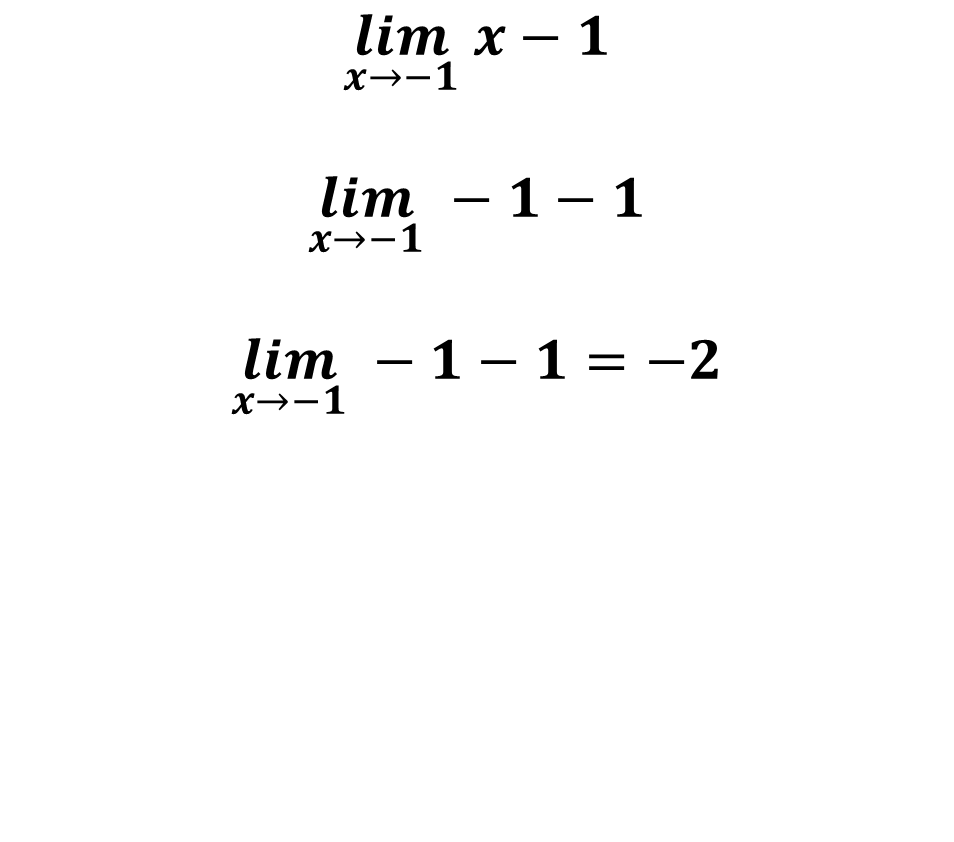
As the limit of the rational function when x tends to -1 gives us -2, that means that the limit exists, therefore there is no vertical asymptote at X = -1, but the rational function is discontinuous for X = -1 of the inevitable type.
The fact that the function does not have a vertical asymptote can be corroborated with the graph generated with the geogebra software:
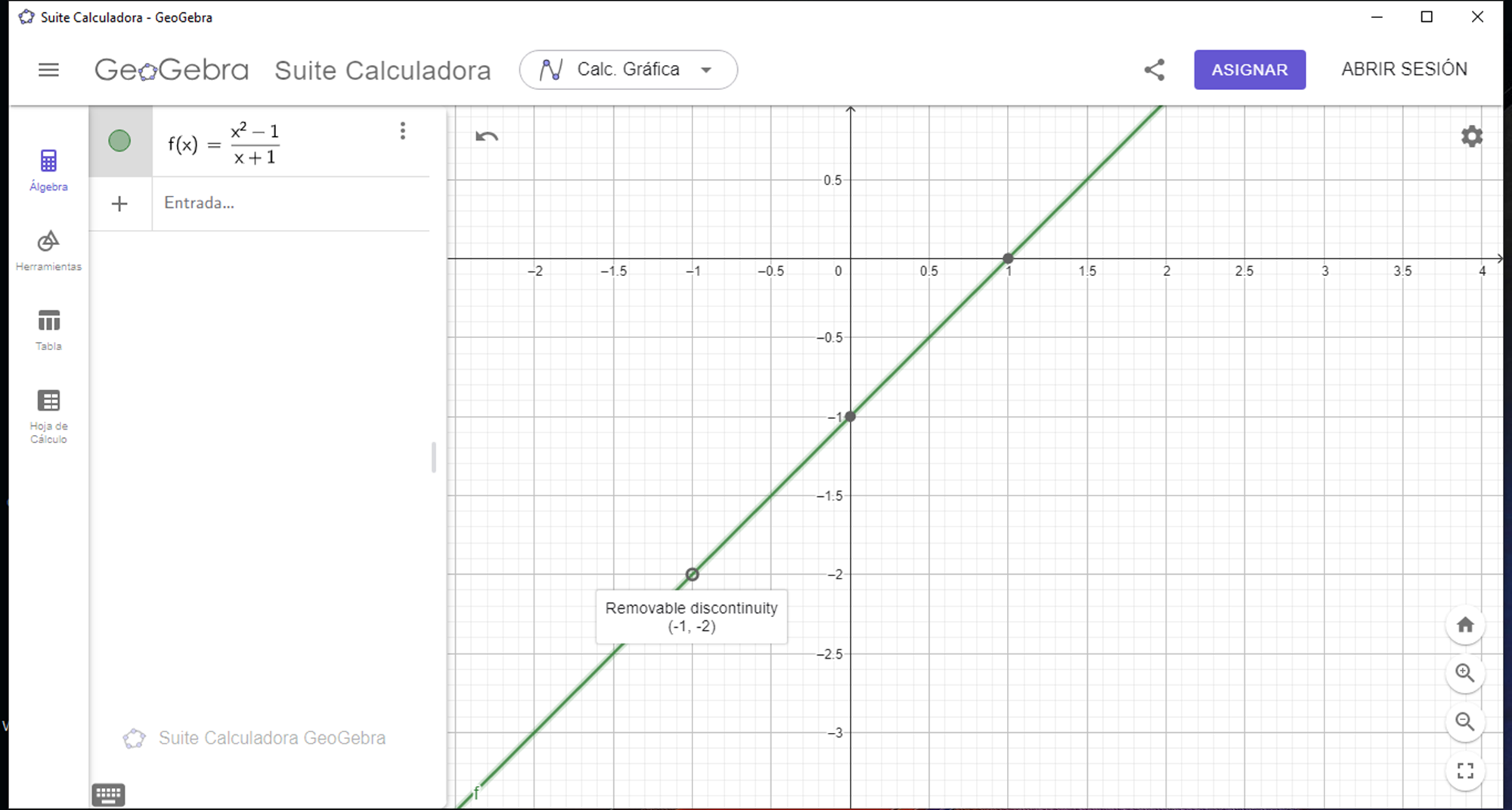
In the graph generated by the geogebra software we can see how there is a removable discontinuity at the point (-1 ; -2), which also affirms that there is no vertical asymptote for x = -1.
For the analysis of the second function:

We have that the value that cancels the denominator is X = -1, reason why we must consider the following limit:

If we make the direct substitution of the limit, we have the following result:
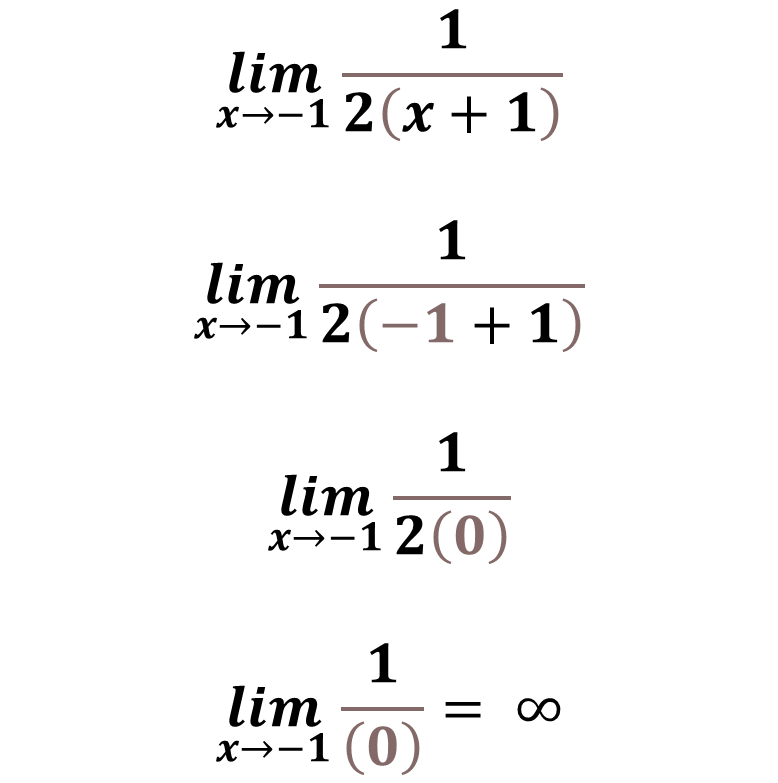
Is it possible to apply some mathematical artifice to break with infinity?
There is no polynomial in the numerator that can be factored to cancel with the denominator, so there is no artifice to apply, which means that the rational function is inevitably discontinuous at X = -1, which serves to interpret that there is a vertical asymptote at X = -1, which we can verify with the following graph generated with the geogebra software:
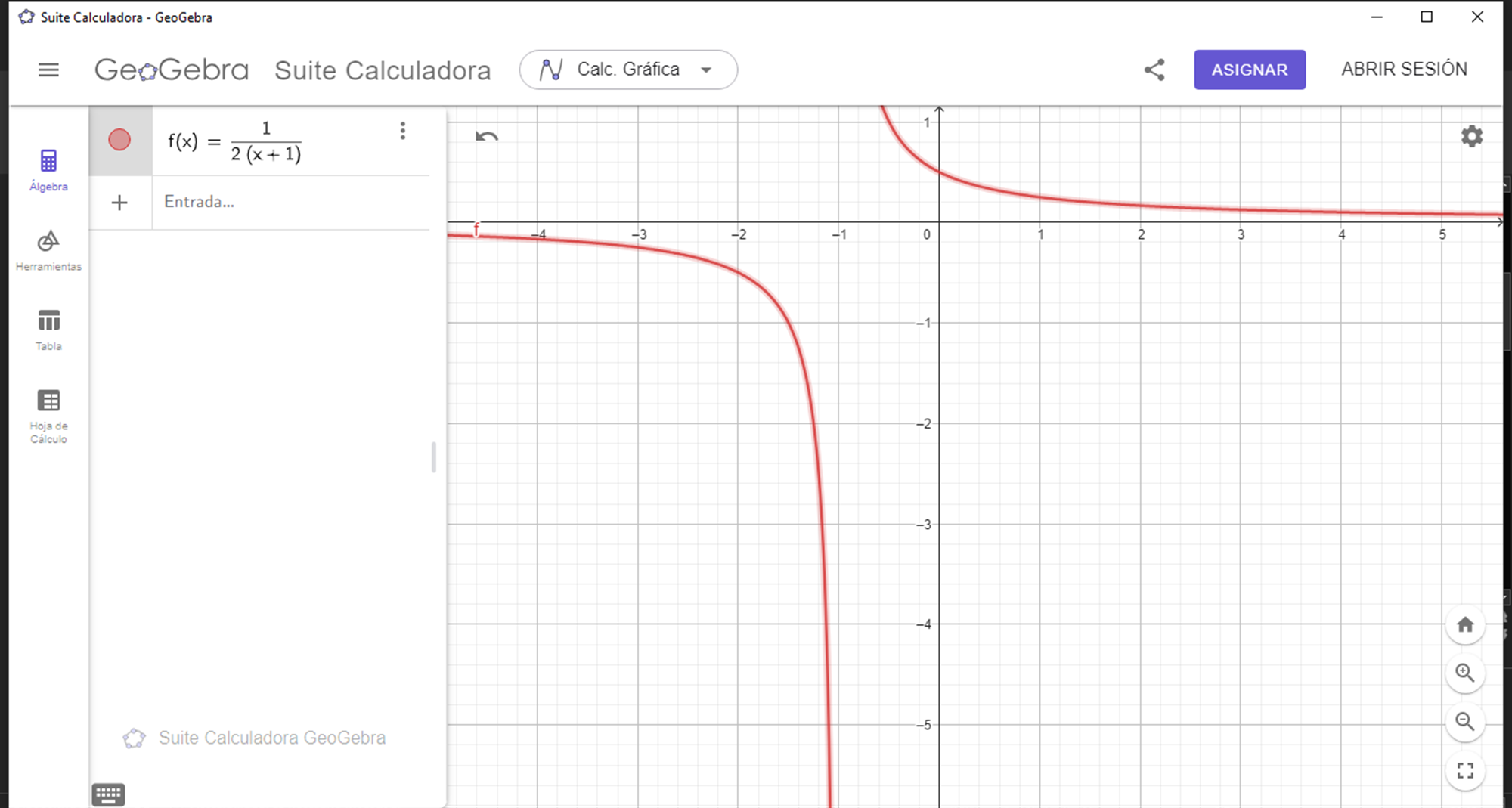
It can be seen how the red curve on the left side sticks to the vertical line X = -1 without cutting it, since at X = -1 there is a vertical asymptote, since at X = -1 the rational function approaches infinity.
Conclusion
When discussing the continuity of a function at a point, it can be deduced that if it is an avoidable discontinuous rational function it is because there is no vertical asymptote, but on the contrary it is an unavoidable discontinuous rational function because there is a vertical asymptote for the value of X where the function tends to infinity.
Recommended bibliography
Calculus with Analytic Geometry. Volume I. 7th edition. Author: Larson and Hostetler.
Note: The equations shown in this post were elaborated using the equation insertion tools of Microsoft Powerpoint, in the generated graphs the geogebra software was used.