Hi there. In this math post, I cover the topic of solving squared equations.
Math text is rendered with LaTeX with Quicklatex.com.
Topics
- Review Of Square Roots
- Solving Equations By Taking The Square Root
- Solving Squared Equations With Examples
Review Of Square Roots
Before getting into solving squared equations I do think it is good to do a review on square roots. A square root is a whole number multiplied by itself to obtain the original number. As an example the square root of 4 is 2 as 2 times 2 is 4. The square root of 100 is 10, the square root of 64 is 8 and so on. Here is a table of common square roots.
| Whole Number | Square Root |
|---|---|
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
| 36 | 6 |
| 49 | 7 |
| 64 | 8 |
| 81 | 9 |
| 100 | 10 |
| 121 | 11 |
| 144 | 12 |
In the table above, the square root is positive. The square root in the table above can also be negative. As an example the square root of 2 is +2 or -2. This is because +2 x +2 = 4 and -2 x -2 = +4.
Solving Equations By Taking The Square Root
The next step is to review solving equations by taking the square root. Here are some examples.
Example One
Solve for x in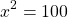 
.
For this question the x-squared is on one side and the number is on the other side. The square root can be taken on both sides. The square root of x-squared is x and the square root of 100 is plus or minus 10.
Example Two
What is the value of x in 
With this one you cannot take the square root of both sides right away. It is important to make sure that one side has just the x-squared and the other side has just a number only. Once that is done, the square root on both sides can be taken.
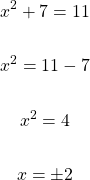
Example Three - Reducing Radicals
Solve for x in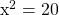 
.
With this one you can take the square root of both sides.
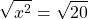
For the number 20, it can be split into smaller number factors where one of the numbers is a perfect square. (See table above left column.) Twenty can be split into 4 x 5 where 4 is a perfect square. We use this property for square roots.
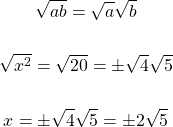
Solving Squared Equations With Examples
The examples from the previous section just had xx part to the other side. Here are some examples for dealing with such cases. No need to expand the square of the binomial.. What if we have something like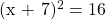 
. It is not that easy to move the numbers to one side and the
Example One
Solve for x in .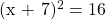
With this one you can take the square root of both sides to start.
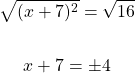
With the plus and minus, there are two cases to consider. One case is dealing with positive four and the second case is with negative 4.
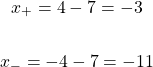
The two solutions for x are -3 and -11.
Example Two
What is the value of x for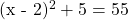 
Start with subtracting both sides by 5.
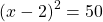
Take the square root of both sides.
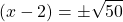
The square root of 50 can be reduced. Seventy-five is 25 x 2 where 25 is a perfect square number.
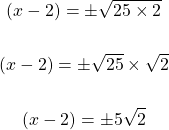
From here, consider the two cases for x. I use the notation of x-plus and x-minus again.
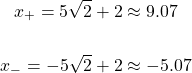
Posted with STEMGeeks
What are these things in these big calculations?
A common and severe mistake is the dreaded negative sign.
Hmm. I see. Arc length? Trigonometric substitution for integrals with square roots?