
Introduction
Hey it's a me again @drifter1!
Today we continue with Mathematics, and more specifically the "Number Theory" series, in order to get into Divisibility Examples. We didn't get into too complicated examples and so there is clearly the need for such a post. Additionally, we will also mention various properties of Divisibility before-hand, which somehow were left out in the original post.
So, without further ado, let's get straight into it!
Properties
Let's consider two natural numbers a and b. When a perfectly divides b, meaning that the result of division is a whole number c, than we say that a divides b or a | b or b = a × c.
Additional properties that hold are the following:
- Any natural number a divides itself or a | a.
- One divides everything or 1 | a for all a.
- One can only be divided by ±1 or a | 1 then a = ±1.
- Any natural number a divides 0 or a | 0.
- Zero divides only zero or 0 / a then a = 0.
- Transitivity: when a | b and b | c then a | c.
- Linearity: when a | b and a / c then a | ka + lb for all k, l. In other words, a divides all linear combinations of b and c. For example, a divides b + c and b - c, which can turn out to be quite useful in calculations!
- Multiplication: when a | b then ca | cb.
- Cancellation: when ab | ac and a ≠ 0 then b | c.
- Comparison: when a | b and a, b are both positive then a ≤ b.
Examples
Let's now get into some examples of Divisibility which don't rely that much on the Divisibility Rules mentioned in the 2nd article of the series, but more on the properties and other proving strategies.
Example 1
Prove that any number of the following format is divisible by 5:

Solution
We basically want to prove that:

This requires proving through a strategy known as Mathematical Induction. For more info on that please check out the corresponding Discrete Mathematics series' article:
Let's first check if the statement holds for n = 1:
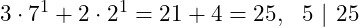
It holds!
Supposing that the statement holds for n we now have to proof that it also holds for n + 1.
As the statement is now true for n, we have:
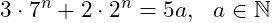
whilst n + 1 has to be proven to be of the form:
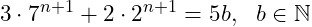
The statement for n can be substituted into the statement for n + 1 as follows:
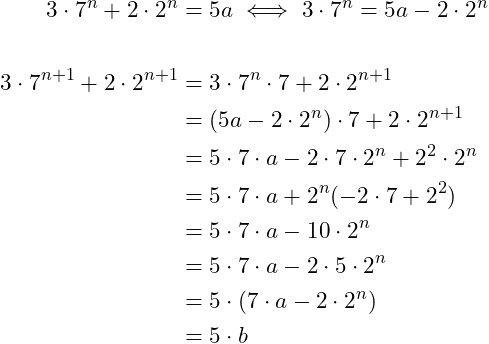
So, the statement holds for n + 1 as well!
Therefore, the statement holds for any natural n.
Example 2
Prove the following statement:
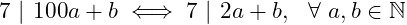
Solution
Dividing 100 by 7 yields 100 = 14 × 7 + 2.
Thus, as 7 | 100a + b:
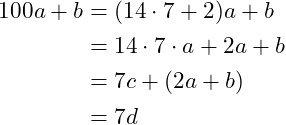
What remains now is proving that 7 | 2a + b.
As 7 | 100a + b = 7c + (2a + b), based on linearity we have:

Now for the opposite...
Supposing that 7 | 2a + b of course 2a + b = 7e. And so:
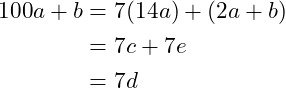
Thus, 7 | 100a + b.
Example 3
Prove that 6 divides the product of any three consecutive integers, (n - 1), n , (n + 1).
Solution
We basically have to prove that 6 | (n - 1) n (n + 1), which can be turned into two simpler sub-problems:
- 2 | (n - 1) n (n + 1)
- 3 | (n - 1) n (n + 1)
as 6 = 2 × 3.
The first one is always true as at least one of the three integers has to be even, meaning that the resulting product will also be even and thus the product divisible by 2.
1, 2, 3 → one even number (1 × 2 × 3 = 6 is even)
2, 3, 4 → two even numbers (2 × 3 × 4 = 24 is even)
For the second sub-problem we have to try all cases of dividing n by 3 and thus n will be:
- n = 3k
- n = 3l + 1
- n = 3m + 2
For n = 3k, the product is divisible by 3 as 3 | (3k-1) 3k (3k + 1).
For n = 3l + 1, the product is again divisible by 3 as now n - 1 = 3l which is divisible by 3.
Lastly, for n = 3m + 2, the product is again divisible by 3 as now n + 1 = 3m +3 = 3 (m+1) which is again divisible by 3.
Thus, the product of three consecutive integers is divisible by 3, finally proving that it's divisible by 6 = 2 × 3.
For example:
5 × 6 × 7 = 210 is divisible by 6.
Of course, 210 is even (divisible by 2).
And 2 + 1 + 0 = 3 which is divisible by 3.
Thus, it's been verified by applying Divisibility rules as well!
RESOURCES:
References
- https://brilliant.org/wiki/number-theory
- https://math.libretexts.org/Bookshelves/Combinatorics_and_Discrete_Mathematics/Elementary_Number_Theory_(Clark)/01%3A_Chapters/1.03%3A_Elementary_Divisibility_Properties
Mathematical equations used in this article, have been generated using quicklatex.
Block diagrams and other visualizations were made using draw.io.
Previous articles of the series
- Introduction → Number Theory, Why Number Theory, Series Outline
- Divisibility → Divisibility, Divisibility Rules
- Factorization and Euclidean Algorithm → Factorization, Euclidean Algorithm and GCD, Division Algorithm using Calculator
- Prime Numbers → Prime, Composite and Co-Prime Numbers, Prime Test (Sieve of Eratosthenes)
Final words | Next up
And this is actually it for today's post!
Not too sure about the next article's topic yet.
See ya!

Keep on drifting!
Posted with STEMGeeks
Well drifted divisibility examples. Thanks for sharing dude.
Nice examples! Thanks for bringing and enlightening us
!1UP
<a href="https://discord.gg/zQrvxAu7mu"> <img src="https://files.peakd.com/file/peakd-hive/thecuriousfool/23wCNFDyCLJu1v77TTg2MYKkd7XWkgF9fhiLujTDAaLaUz7H4AaQkDentB5UMVS8FcrVs.png"></a>You have received a 1UP from @gwajnberg!
@stem-curator
And they will bring !PIZZA 🍕. The @oneup-cartel will soon upvote you with:
Learn more about our delegation service to earn daily rewards. Join the Cartel on Discord.