A couple days back I wrote an article about the interest collar on our home loan and how paying off more now makes a huge amount of sense. Essentially, because we have a collar at a very low rate for the next 8 years, everything extra we put in will shorten our loan. And the earlier we start, the more impact it will have, as it will benefit from the compounding factors that reduce the principle faster, meaning the interest portion will reduce and more will increasingly go to reducing the principle.

I shared the article with my wife, who still hasn't read it, but decided to see if the internet had anything that would allow me to visualize it more easily, which of course there was. Using this to demonstrate it to my wife allowed me to have the conversation and show her in real time what was actually happening. This was very helpful for her, so I thought it would be worth laying out here too.
There are a few tools out there, but I chose this one because it was quite clean looking and updated on-the-fly as changes were made, which sped up the process. I haven't used one of these before, and while I did do various accounting classes at university, I sucked ass and don't remember how to do this myself. This is somewhere I think tools are useful, as there is very low value in me being able to do this myself, but there is very high value in being able to get the results.
So, to be consistent, I am using the same loan size of 200,000 from the other article, and will plug in my interest rate of 1.7%. However, rather than looking at monthly costs and savings, I want to know how paying higher amounts are going to affect the length of the loan. I have chosen 30 years, so 360 monthly payments.
The first one to start with is the baseline, which is paying back what the bank would suggest gets paid back.
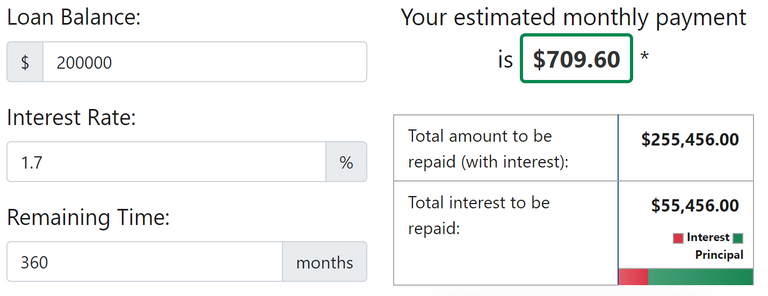
It is very easy to choose to do this at the moment rather than paying more, especially when the economy is tanking, because it keeps money in the hand. However, this is the "trick" with the collar, because this is the longest part of the loan, which means that paying more per month in this period will have more opportunity to compound reduce the principle. However, many don't do this, because often they feel they don't have any extra, as they are younger, likely have lower paid jobs and are starting a family at this point. It gives "security" so the payments are known, but that security comes at a cost of shortening the loan with a multiplier effect.
To visualize the baseline:
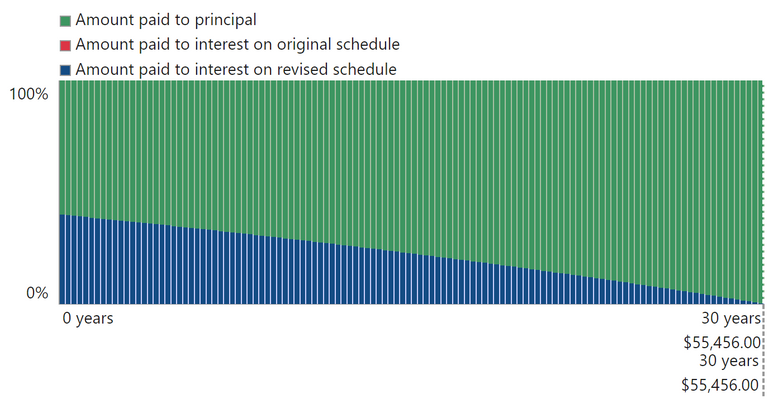
As you can see, there is no "red" in the graph, as we are paying only the suggested amount. The loan will end at the 30 year point, as the bank planned and we would have paid 55,000 in interest. But as you can see, that isn't right, is it? Because we only have a collar for the next 8 years and we have no idea what the interest rate will be past that point. If it is lower, great, but the chances of that are slim I believe. And, even if it goes lower during our collar, we will pay less than the 1.7% also.
Note: After, I will show parts of the amortization table to show what is happening.
But, what if we were to round our payment up to the even thousand, so add 290 a month to our repayment schedule? That is an increase of about 40% in payment amount.
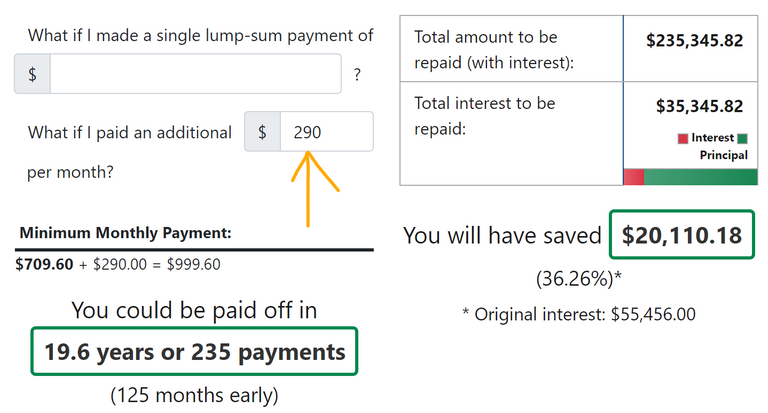
Now, we have saved 20,000 in total interest and we would have reduced the repayment time from 360 months to 235 months. And you can see in the following graph how that looks.
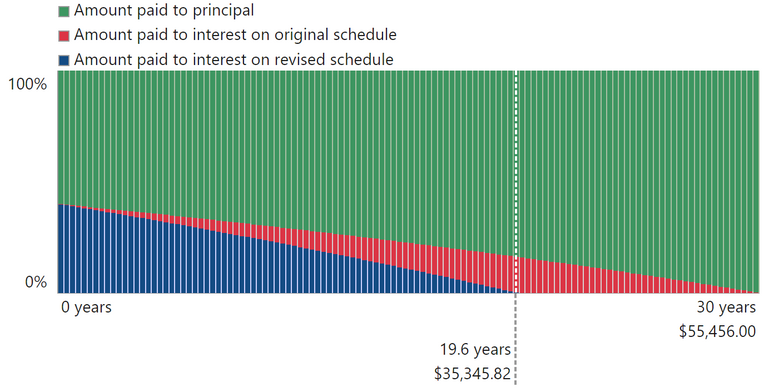
This means that we have reduced our loan length by ten years, or ~33%. But what should be remembered is that this "saving" is more than just on the total interest repayment reduction, because for those ten mortgage-free years, the saving is also the principle payment too. that is 120 months of not paying 1000 dollars a month, so it is 120,000 in savings that could be invested and generate more income.
For instance, if for those ten years the 1000 was invested and gained 10% per year compounded monthly, By the end of the ten years, 120,000 in capital would have been injected and it would be worth 204,000.
Now, you should be looking at that and saying,
"Hey, that is more than the initial house loan"
That is ten years without having a mortgage, making up for the total loan that was going to take 30 years to pay off. Sure, there is some inflation in there too, but you get the idea.
So, what if instead of 290 extra, we scrimped and saved and was able to feed 500 more in a month, so the repayments per month are 1,210.

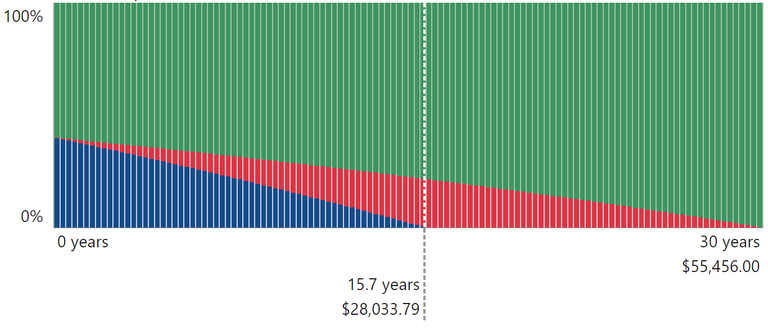
That almost halves the loan, and if we were to do the same as above with the investment, it would be 1,210 for the next 14 years, the monthly contributions would amount to 168,000 and have a value of 363,000.
If this was our loan and we could shorten it like this, I would be 59 when the loan is paid off and would have extra money going in from that point to top up my super (or invest), after paying all of my compulsory anyway.
And just for fun, in order to pay it off at the time the collar ends in 8 years, it would take about 1,450 extra month, so payments of around 2,200.

That is likely undoable for us, so lets assume we can add the 500 and it will take about 16 years. Where does that leave us when the collar comes off and we lose our 1.7% ceiling? For this, we look at the amortization table and what principle is left after the 8 years, which is month 96.
But before we do that, let's look at month 1:

The thing to look at is the green side in relation to the red side. The green is how much comes off the principle, the red is how much is paid in interest.
If we go to 4 years:

We can see that with the same monthly payment, we are paying an additional 64 off per month and this increases each month. By the end of the collar at month 96, it looks like this:

That is 130 extra coming off the principle in that month, compared to month 1.
That means there is still about 105,000 left on the loan to pay, over half. But, we are only 26% of the way through the original 30 year loan period. We have smashed it! But there is still that half to pay, so that means that our payments are going to be adjusted based on the principal left and the interest rate, and it will assume there are still 30 years in total, meaning there are 22 years to go. This is the same as a loan of 105,000 for 264 months and whatever the interest rate is at the time. Let's assume 7% for the whole of the 22 years, which is very high, but what it is in many places now, though it will decrease from there in a couple years most likely.
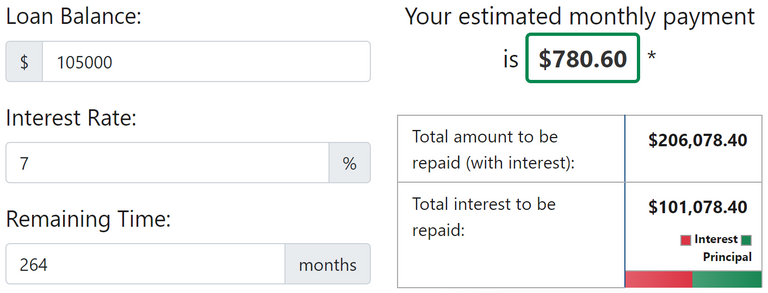
This means that the suggested monthly repayments are 780 dollars and we will finish paying the loan in 22 years, with the interest being almost the same as the 105,000 principle. But, remember we were used to paying 1210 a month with that extra 500 before, so we would continue to do that during this period too. So keeping the same payment we have been making for the last 8 years of 1,210, it would look like this.
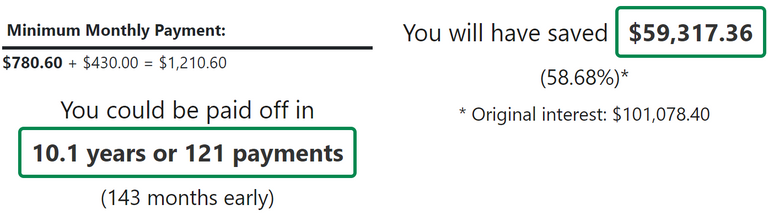
A 22 year loan is now a 10 year loan. This means that the total loan of 30 years has been reduced to 18 years, even though the last ten years of that was all at a very high 7% interest rate. And, all of that time, it was the same repayment amount every month, meaning that it was very easy to calculate for those years. And of course, the interest rate on those last years might be significantly lower than 7%, but it is good to factor it at that level, as that is a percentage or two above what they calculate for loan stress testing.
And yes, it might not be possible for everyone to pay back a huge amount extra on their loan each month, but consider the same loan of 200,000 with a static 5% interest rate for 30 years.
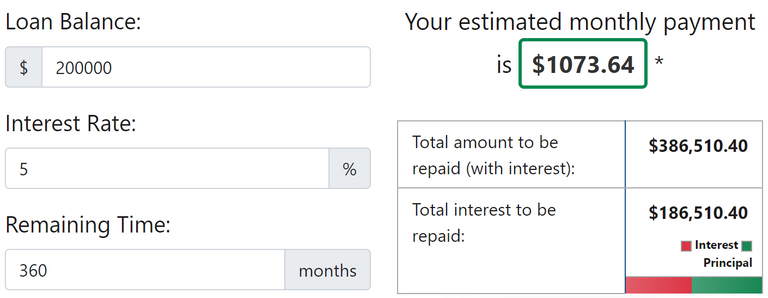
That is a monthly repayment of 1073.
If we round to the next 100 and add 27 dollars a month:

That is 20 months cut off the loan, a saving of 11,885 in interest and, 20x 1100 in the pocket, or 22,000 in that time.
What can you buy for 27 dollars?
(or relative depending on your location)
If we round it to the next 100 and pay 1200 a month:

That is almost 6.5 years early, a saving of 44,500 in interest payments and for those years, 75x 1100, or 82,500 cash in total available to invest. Doing the same thing and putting it to investments that earn 10% calculated monthly, after 75 months (6.25 years), it would be worth 114,000.
So, instead of just paying off the mortgage after 30 years and freeing up that 1073 a month, you would have paid off the mortgage years earlier and have 114,000 in your pocket instead.
Worth paying a little extra now?
Taraz
[ Gen1: Hive ]
Posted Using LeoFinance Alpha
There's always more to "need." I think the problem with owning a home isn't always the loan. It's usually the cost of keeping up with everything else, the unforeseen this or that. Add kids and there is always some way to "better" spend the money.
If I sell the kids however, I think I could maybe work this strategy in.
However, the difference of a pizza month can be the difference between a 30 year loan and a 20 year loan. There are always things to spend on, but I also think that for most of us, there is a lot of wastage too and often on things that don't bring that much value.
Sounds like a no-brainer to me. Any amount paid extra saves quite a bit in interest payments. I had always heard that paying one extra payment per year of a 30 year mortgage would shave seven years off of those 30 years. I never did this though. I don't know if this happens in Finland, but in the US, those interest payments (not principle payments) are tax-deductible, so you have to take the tax "savings" (taxation is theft) off your savings in interest.
I will have to look more into the tax implications here, as I don't know them in detail. Time to go to the tax website!! :D
Wow, that's a lot of numbers. I wanted to do something similar to that but decided it would be a good idea to build an emergency fund and possibly pay the car off first since that would take much less time and money and I could apply the car payment to the house afterward.
This is a good move and what we are planning too. The loan on the car isn't much, but it will add a large amount to this period of time with the collar, so knocking that out and paying it in will speed our process.
This is very cool but we don't have opportunity or access to take loans like this in my country
I wish we could...
I wonder what it looks like if there was no such thing as taking a loan.
I think this could be done if there is a forescast that the inflation will go down in the future.
If it doesn't go down, there is more reason to pay it off fast. If it does go down, there are still the benefits of paying it off faster.
There is also a method called "velocity banking" that uses short-term higher interest loans to pay off larger loans, like your mortgage in a shorter time. You use a second, high interest loan to pay big chunks of the large first loan,. Then you aggressively pay off the the higher interest loan. It works better if the second loan is a revolving line of credit which you also use to pay down your monthly expenses. By dumping your paycheck into the line of credit, you are reducing the amount of interest you pay on the second loan. And by paying big chunks at a time, you are lowering your overall interest on the second loan too. People are able to pay off both loans in a shorter period doing this.
There are a bunch of videos on YouTube about velocity banking. Some people even use credit cards to do this.
This is done through credit cards too, where all expenses go on credit and then before the end of the month, the card is paid off so there is no interest. I am considering doing this :)
I recently tried out the emergency savings and the retirement calculator. I realized that a lot of those calculators don't count the scenarios like pandemic and the often regular recessions. So this kind of makes you wonder how the impact on the overall calculators over 10 year horizon would make.
It doesn't matter what the long-term is in this case. We know what it is now and we can predict what it will be in 6 months. Even if only able to do this for a year, it would make a significant dent on the future. No one knows what happens tomorrow - there could be a massive EMP that destroys all records and everyone is at zero! :D
Damn that seems like insanely long time for paying a loan. I imagine that after paying it of you will have one of the biggest celebrations in your life. No doubt it will be a milestone.
It is a very long time, but I used it here as that is likely about the average for a house loan. In some places they have more, some the max is 25.
It is also the decision I would make because you don't really want to keep bad debt around. If that money isn't making you money, then it's a liability and reducing as much as you can will help. It will make everything much easier if you are able to save some of the money by spending more money.
Putting it in now and reducing the loan faster, would effectively mean having an even lower rate over the period of the loan. I am also hoping I might get a pay rise somewhere too, so some of that will go in also.
Lending Interest Rate
Dear @tarazkp !
What do you think of the loan interest rates in the world where I live?
Quite low.
Dear @tarazkp !
I was surprised by the high interest rates on loans in Europe!😯
!DHEDGE
Buy DHEDGE on Tribaldex or earn some daily by joining one of our many delegation pools at app.dhedge.cc.This post has been selected for upvote from our token accounts by @valggav! Based on your tags you received upvotes from the following account(s):- @dhedge.bonus- @dhedge.leo@valggav has 0 vote calls left today.Hold 10 or more DHEDGE to unlock daily dividends and gain access to upvote rounds on your posts from @dhedge. Hold 100 or more DHEDGE to unlock thread votes. Calling in our curation accounts currently has a minimum holding requirement of 100 DHEDGE. The more DHEDGE you hold, the higher upvote you can call in.
It is always worth it to pay a little extra for sure to reduce that compounding interest working against you. The visuals you provide are a great example of that. I haven't really taken very many loans in my life, really only one major loan I can think of, and I had a 5-year interest-free provision in mine. I was able to make it work and was able to pay off the full note in exactly the 5-year timeframe and never paid a cent of interest. In fact, to this day, I've only paid interest twice, and that was because I forgot to make my credit card payment on time -- and both times I got that sorted so I only ended up paying interest for that one month I missed.