Planteo la solución de una serie de ejercicios propuestos para que el lector afiance los conocimientos que ha recibido en las entregas anteriores, como una especie de clase práctica. La mayoría de ejercicios han sido tomados y adaptados del libro de Blank y Tarquin, ediciones del 2006 y del 2007. Explícitamente, indicaré las fuentes de los ejercicios donde se requiera. Además, aprovecharé este artículo para introducir el tema de la capitalización interperiódica y de algunas reglas prácticas que se aplican cuando no existe tal modalidad en los proyectos de inversión. Es un artículo pensado como material de apoyo para mis estudiantes, pero cualquier lector independiente que siga esta serie podrá comprenderlo también.
Ejercicio 3.1 –Tomado y adaptado del Ejemplo 4.4 de Blank y Tarquin (2006)
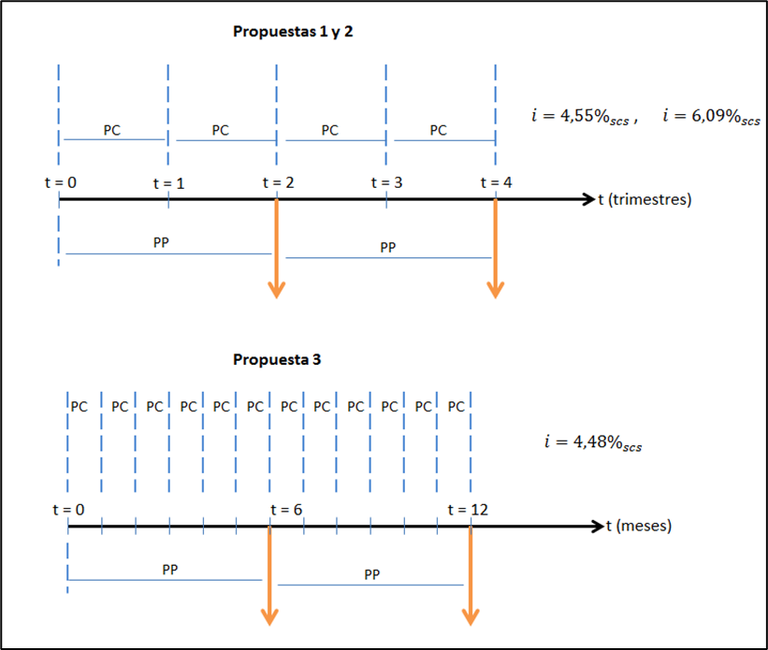
ABC es una empresa que abastece de partes importantes a los fabricantes de automóviles. Un ingeniero pertenece al comité de ABC que evalúa propuestas para incorporar maquinaria de medición de nueva generación al proceso de producción de partes de alta precisión. Tres propuestas de venta incluyen las tasas de interés que se indican a continuación. ABC hará pagos semestrales únicamente. El ingeniero se encuentra confundido respecto de las tasas de interés efectivas que rigen cada alternativa.
Propuesta 1: 9% anual, compuesto trimestralmente.
Propuesta 2: 3% trimestral con capitalización trimestral.
Propuesta 3: 8,8% anual con capitalización mensual.
a) Determina la tasa efectiva de cada propuesta si se harán pagos semestrales y construye los diagramas de flujo de efectivo para las tasas de las diferentes propuestas.
b) ¿Cuáles son las tasas anuales efectivas?
Solución

Ahora, para cada caso, se dispone de una tasa de interés con períodos de referencia y de capitalización iguales. En consecuencia, es posible aplicar la ecuación 2.3 para hallar la tasa de interés semestral con capitalización semestral equivalente a la que se tiene en cada propuesta.
Figura 3.1.
Ejercicio 3.2 –Tomado y adaptado del Ejemplo 4.6 de Blank y Tarquin (2006)


Un consultor realizó depósitos en una cuenta especial para cubrir algunos gastos futuros. La Figura 3.2 muestra el diagrama de flujo de efectivo correspondiente, desde el punto de vista del consultor que desembolsa los depósitos (también podría haberse dibujado desde el punto de vista de la cuenta que recibe los depósitos) ¿Cuánto hay en la cuenta 10 años después, si la tasa de interés es del 12% anual y se capitaliza semestralmente?
**Figura 3.2.
**
**Solución
**
En primer lugar, debemos convertir la tasa de interés dada a una tasa efectiva anual porque los flujos de efectivo ocurren exactamente al finalizar los años respectivos.
ocurre (t = 4) hasta el momento en que debes evaluar el valor final (t = 10); y algo similar pasa con el monto de 1.500 USD, desde t = 6 hasta t = 10: transcurren cuatro años. Reitero: el razonamiento que siempre debes tener presente es que el dinero tiene un valor en el tiempo, por lo que no puedes sumar o restar flujos de efectivo, a menos que los hayas trasladado antes, con la tasa de interés que corresponda, a un mismo punto en el tiempo.
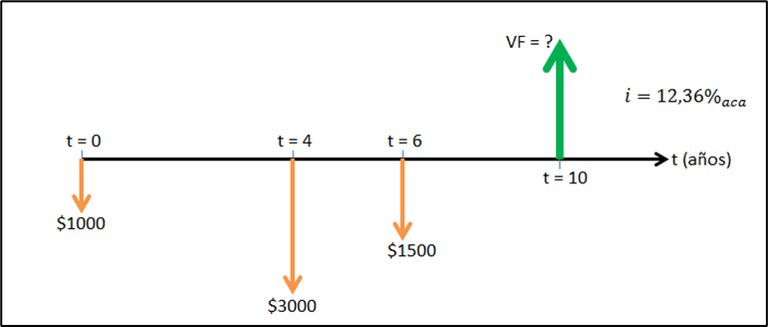

Otra observación importante es que los flujos de caja se han marcado como negativos en la ecuación. Esto es simplemente una convención que sugiere que los tres flujos de caja invertidos representan desembolsos de dinero. Por una razón de homogeneidad, el valor final da negativo también, pero lo relevante acá es reconocer que, al final del año 10, los 11.634,5 USD estarán disponibles para que el consultor disponga de ellos.
Ejercicio 3.3
El mantenimiento de un proceso productivo ha costado de manera constante 140.000 USD en cada uno de los últimos cinco años. Si la tasa de interés fue del 8% anual durante los primeros tres años y luego se incrementó a 10% en los años 4 y 5, ¿cuál es el valor futuro equivalente (en el año 5) del costo de mantenimiento? Muestre el diagrama de flujo de efectivo pertinente.
Solución
La Figura 3.3 muestra el diagrama de flujo de efectivo correspondiente al escenario descrito.
Cada flujo de efectivo debe trasladarte al instante t = 5 para poderse sumar con el resto y obtener el valor futuro. Recuerda que como los flujos de efectivo ocurren en instantes de tiempo distintos no pueden sumarse o restarse directamente, dado que el dinero tiene un valor en función del tiempo. La traslación se hace considerando la tasa de interés apropiada para cada período. Observa que este ejercicio contempla el uso de tasas que varían.
El signo menos sólo sugiere que es un valor futuro desembolsado que corresponde a todos los flujos erogados en el desarrollo del proyecto.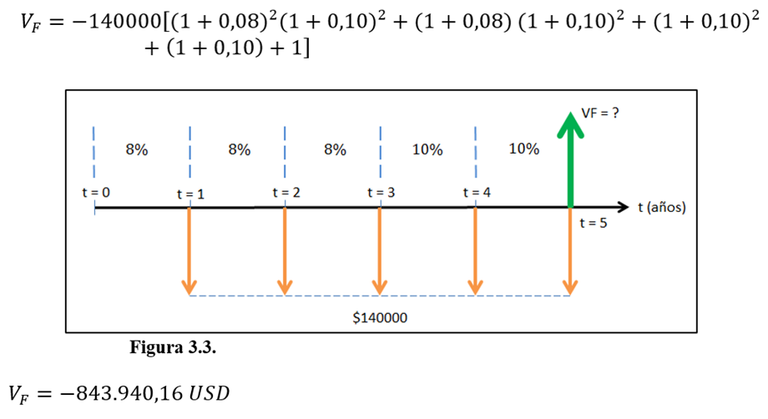
**Ejercicio 3.4 -Tomado de Blank y Tarquin (2007)
**
Si se llenan nanotubos de carbono con alambres minúsculos de fierro y carburo de fierro, es posible extruir nanoalambres increíblemente delgados por medio del impacto de los nanotubos de carbono con electrones. Si Gentech Technologies planea gastar 1,7 millones USD en el año 1, 2,1 millones USD en el año 2 y 3,4 millones USD en el año 3 para desarrollar la tecnología, determine el valor presente de las inversiones en el año 0 si la tasa de interés en el año 1 es de 10%, y en los años 2 y 3 es de 12% anual con capitalización anual. Construya el diagrama de flujo respectivo.
Solución
**Figura 3.4.
**
En este ejemplo, el monto de 1.700.000 USD, que ocurre en t = 1, da “un solo salto hacia atrás” para poderse ubicar en t = 0 con una única tasa de interés, la del 10 %; por esta razón, el denominador de la primera fracción es (1+0,10) elevado a la potencia uno. El segundo monto, 2.100.000 USD, que ocurre en t = 2, debe dar “dos saltos hacia atrás” para poder ubicarse en el punto t = 0: un año con la tasa de interés del 12% hasta t = 1, razón por la cual aparece en el denominador (1+0,12) elevado a la potencia uno; y otro año con la tasa de interés del 10% tasta t = 0, razón por la que aparece en el denominador (1+0,10) elevado a la potencia uno también. Observa el denominador del tercer monto, el que ocurre en t = 3, e intenta interpretar por qué contiene el factor (1+0,12) elevado a la potencia dos y el factor (1+0,10) elevado a la potencia uno.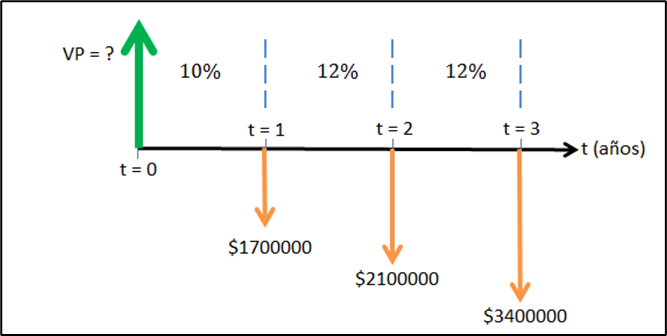

**Capitalización interperiódica **
Cuando el período de pago (PP) es menor que el período de composición (PC), cada flujo de efectivo puede o no capitalizarse. Si lo hace, se dice que existe capitalización interperiódica; si no, lógicamente, no existe.
Cuando no existe capitalización interperiódica o entre períodos, la norma convenida es la siguiente: cada flujo de salida (erogación o flujo negativo) se mueve al final del período de composición mientras que cada flujo de entrada (ingreso o flujo positivo) se mueve al principio de ese período. Una vez hecho esto para todos los flujos interperiódicos se procede a aplicar la tasa de interés efectiva en el período de capitalización dado.
Cuando sí existe capitalización interperiódica, transformamos la tasa de interés del período de capitalización a una tasa de interés para el período de pago y la aplicamos para hallar el valor futuro o el valor presente.
Ejercicio 3.5 –Problema 4.47 de Blank y Tarquin (2007)
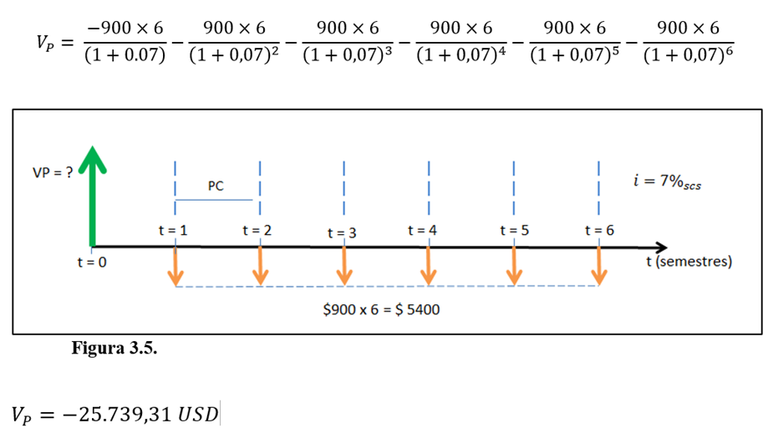
El camión Autocar E3 de recarga tiene un sistema de recuperación de energía desarrollado por Parker Hannifin LLC que se espera reduzca 50% el consumo de combustible. El fluido presurizado pasa de los tanques acumuladores de fibra de carbono reforzada a dos motores hidrostáticos que impulsan el vehículo hacia adelante (el camión recarga los acumuladores cuando frena). El costo de combustible para un camión regular de recarga es de $900 por mes. ¿Cuánto puede desembolsar una compañía privada de tratamiento de residuos ahora si quiere recuperar su inversión en tres años más un rendimiento de 14% anual con capitalización semestral? Suponga que no hay capitalización interperiódica.
Solución
La Figura 3.5 muestra el diagrama de flujo de efectivo correspondiente al escenario descrito. Este diagrama considera que los costos de combustible ya fueron trasladados al final de cada período de composición (semestre) por ser erogaciones y no existir capitalización interperiódica. Por esa razón aparece en el numerador de cada fracción siguiente 900 multiplicado por 6, y ese total se asume trasladado hasta el final de cada semestre. Además, como el horizonte de inversión es de tres años, según se indica en el enunciado, el diagrama de flujo de efectivo se dibuja hasta el semestre t = 6.
Luego, el valor presente de todos esos flujos de caja se obtiene con la tasa efectiva pertinente: una del 7% semestral con capitalización semestral (que deriva de la dada del 14% anual con capitalización semestral, dado que hay dos semestres en un año).
Ejercicio 3.6 –Tomado del Ejemplo 4.11 de Blank y Tarquin (2007)
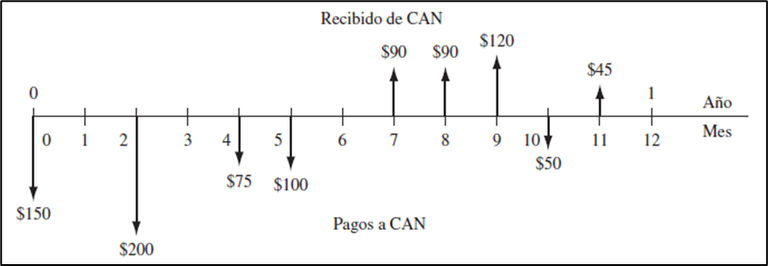
El año pasado, la empresa AllStar Venture Capital acordó invertir fondos en Clear Air Now (CAN), compañía nueva en Las Vegas que surgió de investigaciones sobre ingeniería mecánica en la Universidad de Nevada. El producto es un sistema nuevo de filtración que se emplea en la captura y conservación de carbono (CCC) en las plantas carboeléctricas. El administrador de los fondos generó el diagrama de efectivo que se muestra en Fig. 3.6 en unidades de $1000, desde el punto de vista de AllStar. Se incluyen pagos (flujos de salida) para CAN realizados en el primer año y recepciones (flujos de entrada) de CAN para AllStar. En el primer año no se esperan ingresos; sin embargo, el producto es promisorio y hay pedidos anticipados de plantas del este de los Estados Unidos que buscan operar sin ninguna emisión. La tasa de interés es del 12% anual con capitalización trimestral y AllStar usa la política de no aplicar intereses interperiódicos. ¿Estará AllStar en “números rojos” al final del año? De ser afirmativa la respuesta, ¿por cuánto?
**Figura 3.6.
**
Solución
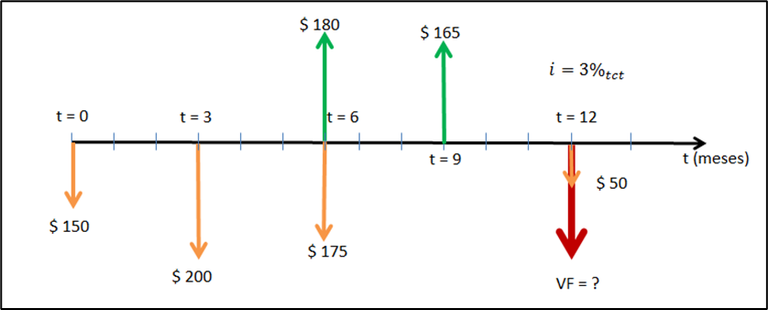
La tasa anual con capitalización trimestral del 12% dada equivale a una trimestral con capitalización trimestral de 3%, porque hay cuatro trimestres en un año.
Por otro lado, debido a que no existe capitalización interperiódica, cada egreso se mueve íntegramente al final de cada período de composición (trimestre, en este caso) y cada ingreso al inicio de éste, según la norma convenida. Así, el diagrama de flujo resultante es el que se indica en Figura 3.7.
**Figura 3.7.
**
Observa que los flujos de caja que ocurren justamente en los períodos de composición no se mueven; sólo se movilizan los que ocurren entre períodos. Veamos ahora cuál es el valor final del proyecto considerando que cada ingreso como positivo y cada egreso como negativo:
¡El proyecto sí estará en “números rojos” al cabo del primer año, por 262.117 USD!
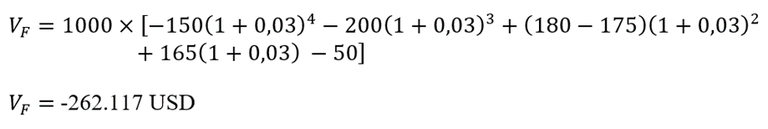
Referencias
Blank, Leland y Tarquin Anthony (2006): Ingeniería Económica. Sexta edición. Editorial Mc. Graw Hill, México.
Blank, Leland y Tarquin Anthony (2007): Ingeniería Económica. Séptima edición. Editorial Mc. Graw Hill, México.
Posted Using InLeo Alpha

Congratulations @vision4s! You have completed the following achievement on the Hive blockchain And have been rewarded with New badge(s)
Your next target is to reach 20 posts.
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPCheck out our last posts: