
En el argot financiero, es común designar con el nombre de anualidad a una serie uniforme periódica, incluso cuando el conjunto de flujos de caja (egresos o ingresos) de igual magnitud ocurra en períodos que no necesariamente sean de un año.
En la entrega anterior, expliqué cómo calcular el valor presente y el valor futuro de una anualidad vencida u ordinaria, esto es, de una anualidad en la que los flujos de caja iguales ocurren al final de cada período y no al principio. En este artículo, explicaré cómo se calculan los valores presente y futuro de dos tipos particulares de series uniformes: las anualidades anticipadas y las anualidades diferidas.
Anteriormente, mencioné que es posible calcular el valor del pago o ingreso periódico de una anualidad ordinaria dados el valor futuro, la tasa de interés compuesto efectiva y el número de períodos (o dados el valor presente, la tasa de interés compuesto efectiva y el número de períodos también). Es evidente que cualquiera de las cuatro variables involucradas en el cálculo puede ser determinada a partir de las otras tres. Ilustremos esto con un ejemplo.
Ejemplo 6.1 (Adaptación del problema propuesto 23 del capítulo 2 de Baca (2007))
Un matrimonio compró una casa de 180.000 $ mediante una hipoteca que cobra 10% de interés anual efectivo. Si el matrimonio puede dar pagos de 23.000 $ cada fin de año, comenzando un año después de la compra, a) ¿cuándo terminarán de pagar la casa?; b) si dan una inicial de 35.000 $ y desean pagar la casa en el mismo plazo calculado en el inciso anterior, ¿a cuánto ascenderán ahora los pagos anuales?
Solución
a) Observa que los pagos son siempre de la misma magnitud (23.000 $) y el período de pago siempre es el mismo (un año). Además, nota que el primer pago se eroga al final del primer año, y que la tasa de interés es compuesta y distinta de cero. En virtud de todo lo anterior, estamos ante una anualidad vencida y podemos aplicar la fórmula (5.1) del artículo 5 de Semillas financieras para despejar de allí el número de períodos:
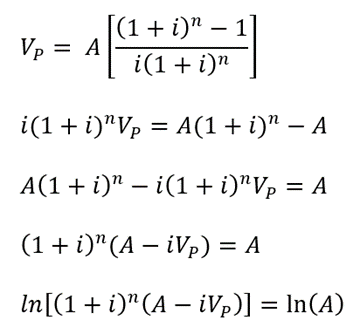
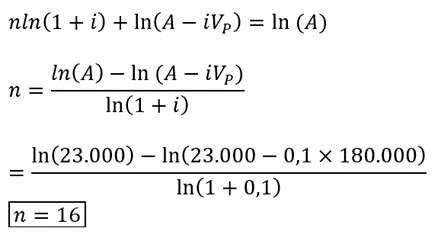
Terminarían de pagar la casa en 16 años.
b) Si dan una inicial de 35.000 $ (en el momento cero pagan la inicial), la serie uniforme periódica o anualidad tendría ahora un valor presente de 180.000 $ - 35.000 $ = 145.000 $. Podemos aplicar la ecuación (5.1) de nuevo y despejar “A”, que representa el monto de los nuevos pagos anuales:
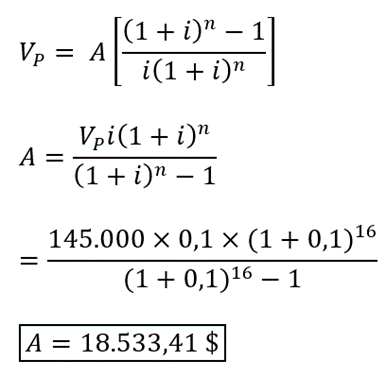
Las cuotas anuales serían ahora de 18.533,41 $.
Anualidades anticipadas o adelantadas
Hasta ahora, he presentado series uniformes periódicas en las que los flujos de caja ocurren al final de cada período. Sin embargo, se llaman anualidades anticipadas aquellas series uniformes periódicas caracterizadas por el hecho de que los flujos de caja ocurren al principio de cada período, no al final. En la práctica, esto podría corresponderse con una situación de pago de alquiler, por ejemplo.
Figura 6.1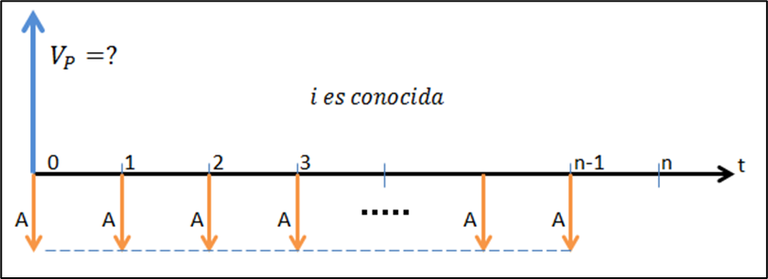
Figura 6.2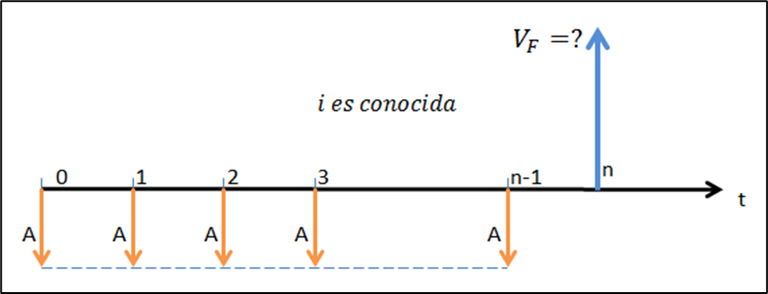
Las figuras 6.1 y 6.2 ilustran los escenarios típicos para el cálculo de valor presente y valor futuro de anualidades anticipadas. En el primer caso, observa que el primer flujo de caja ocurre en el instante cero (y también está allí la flecha del valor presente); el último pago –por su parte– está dibujado en el instante “n – 1”, no en el instante “n”, como ocurría con las anualidades vencidas. En el segundo caso, el valor futuro está dispuesto un período después del último pago.
Si comparas la figura 5.1 del artículo anterior con la 6.1 de esta entrega, notarás que son muy similares. La única diferencia es que los flujos de caja “A” de la figura 5.1 están desplazados un período hacia adelante con respecto a los de la figura 6.1. En otras palabras, cada “A” de la figura 5.1 equivale a un “A(1+i)” de la 6.1. Luego de mover un período hacia adelante los flujos de caja, la figura resultante es la 6.3, que representa una anualidad vencida con pagos regulares de magnitud A(1+i).
Figura 6.3
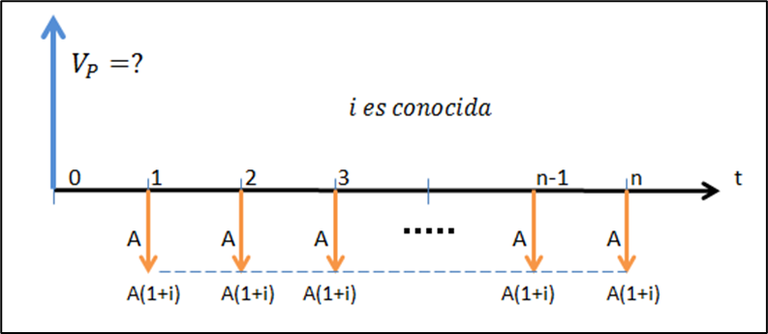
En consecuencia, su valor presente puede calcularse aplicando la ecuación (5.1):
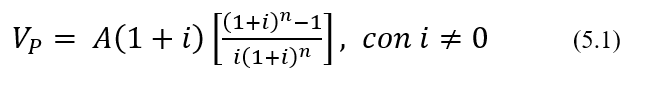
En lo que respecta al cálculo del valor futuro, el razonamiento para convertir la serie anticipada en una vencida es el mismo (figura 6.4); se aplica luego la ecuación (5.2):
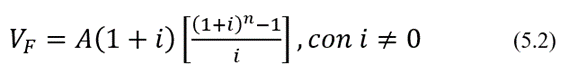
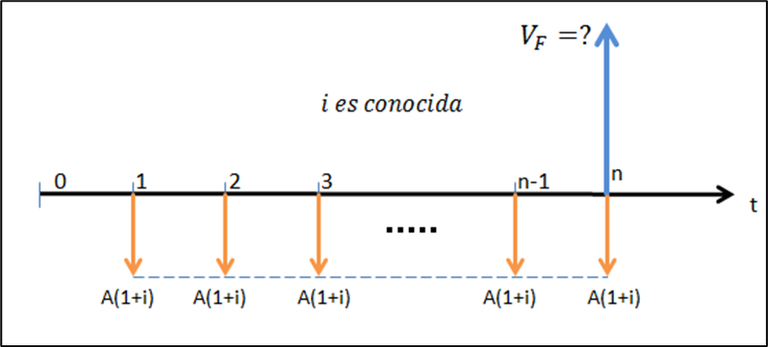
Figura 6.4
Anualidades diferidas
Se caracterizan por tener un plazo que no comienza sino hasta después de haber transcurrido cierto número de períodos de pago. Pueden ser, a su vez, vencidas o anticipadas.
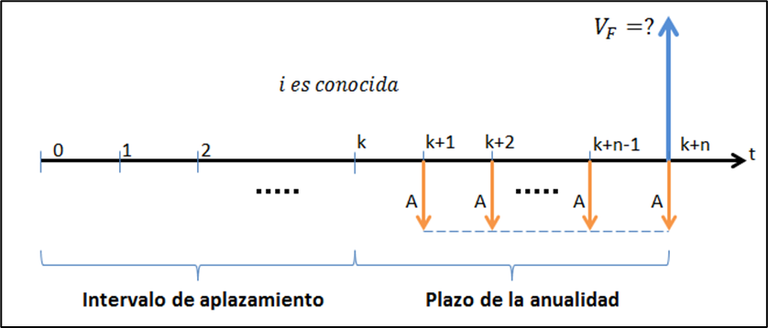
Figura 6.5
La figura 6.5 resume el problema típico del cálculo del valor futuro de una anualidad vencida diferida durante “k” períodos de pago (intervalo de aplazamiento). De forma muy similar, se puede dibujar el escenario para el cálculo del valor presente de una anualidad de este tipo.
Ejemplo 6.2
Después de cinco años, y al final de cada año, pensamos invertir 10.000 $. ¿Qué cantidad tendremos dentro de 20 años si la tasa de interés efectiva que nos otorgan es del 8% anual?
Solución
Como en los cinco primeros años no se efectúan desembolsos y éstos se hacen al final de cada año, estamos en presencia de una anualidad vencida por quince años: el final del año cinco sería nuestro t=0. En consecuencia:
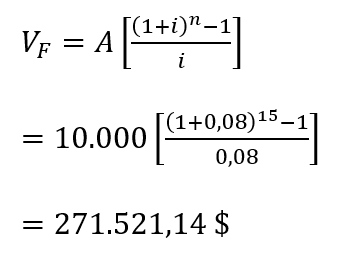
Ejemplo 6.3 (Tomado y adaptado de Garay y González (2007))
La señora Ana Martínez tiene 70 años de edad y una esperanza de vivir 20 años más. Quiere invertir 45.000.000 UM (unidades monetarias) en un fondo que le permita recibir una anualidad constante hasta el final de su vida. Si la tasa de interés es del 19% anual con capitalización anual, ¿cuál será el pago anual que recibirá la señora Martínez? ¿Cuál sería el pago mensual?
Solución
Se trata de una anualidad constante, por lo que se aplica la ecuación (5.1) y se despeja “A”:
Ese sería el pago anual. Para hallar el pago mensual, debemos convertir la tasa de interés aplicando la ecuación de conversión de tasas equivalentes, vista en el artículo 2 de Semillas financieras: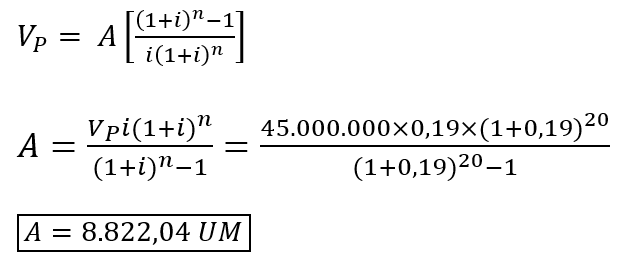
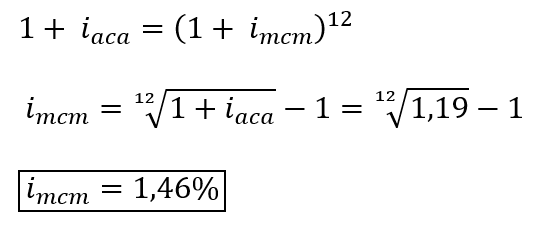
Luego, el plazo de 20 años se transformaría en uno de 240 meses (20x12), de tal forma que “A” ahora valdría:
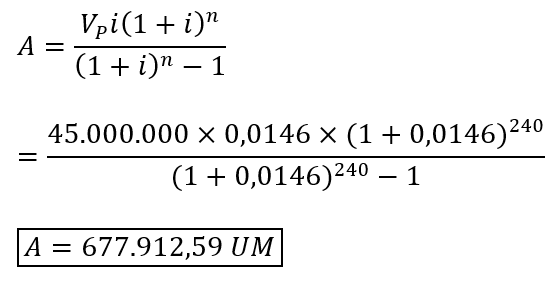
Referencias
Baca, Gabriel (2007): Fundamentos de Ingeniería Económica. Cuarta edición. Editorial Mc. Graw Hill, México.
Garay, Urby y González Maximiliano (2007): Fundamentos de Finanzas con aplicaciones al mercado venezolano. Segunda edición. Ediciones IESA, Caracas.
Posted Using InLeo Alpha
Posted Using InLeo Alpha
Posted Using InLeo Alpha
@tipu curate 8
Upvoted 👌 (Mana: 0/67) Liquid rewards.