
En entregas anteriores, he publicado cómo calcular el valor presente y el valor futuro de un proyecto o de una inversión con flujos de efectivo que no son iguales y que no ocurren periódicamente. Sin embargo, es también común en la práctica encontrar escenarios con ingresos y egresos cuyos valores se mantienen constantes y ocurren (o se estima que ocurran) de forma periódica. Aunque podríamos calcular los valores presente y futuro para estas sucesiones de flujos de efectivo uniformes y periódicas de la forma en que lo hicimos en entregas anteriores, computacionalmente sería más óptimo calcularlos aplicando las técnicas que explicaré en este artículo. Esta guía de estudio es una continuación de las guías anteriores publicadas como Semillas financieras.
Valor presente de una serie uniforme periódica
Imagina que debes pagar (o recibir) la misma cantidad de dinero durante un número determinado de períodos, digamos, anuales. Podrías determinar el valor presente de esa serie de pagos (o ingresos) descontando, hasta el día de hoy, cada flujo de efectivo y luego sumar todos esos descuentos, pero el cálculo se complicaría si la vida de la serie se extendiera por muchos períodos (30 años, por ejemplo).
Recordando algunas herramientas matemáticas, es posible obtener una fórmula mucho más sencilla para calcular el valor presente de una serie uniforme periódica con “n” períodos de tiempo. Considera la serie de pagos que se muestra en la figura 5.1.
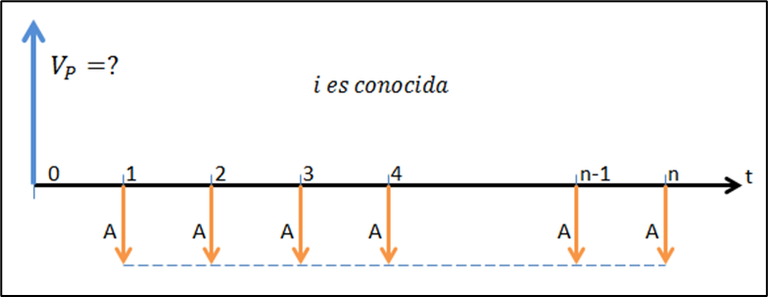
Figura 5.1.
Si quisiéramos determinar el valor presente de la serie uniforme periódica, la ecuación sería:
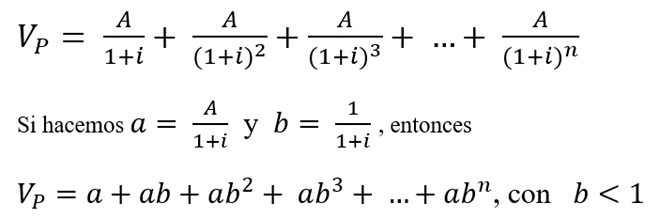
En este caso, por tratarse de desembolsos de dinero, A < 0. Nota, además, que el resultado anterior es una serie geométrica con primer término “a” y razón constante “b”. La suma de los “n” primeros términos de una serie de esta naturaleza vale:
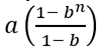
Luego, el valor presente sería:
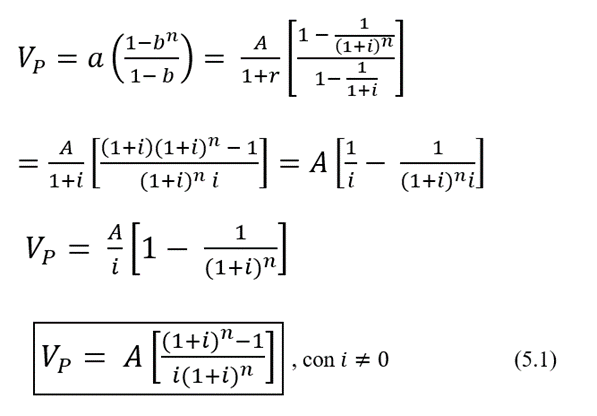
Observa que dados A,n,i puedes obtener el valor presente, y que dados el valor presente,n,i puedes obtener A. “A” se conoce en ingeniería económica como valor anual uniforme equivalente. De la figura 5.1 es importante resaltar también que el valor presente que se desea calcular debe siempre estar situado un período antes de la primera A para que la ecuación (5.1) sea válida.
Valor futuro de una serie uniforme periódica
La figura 5.2, por su parte, se corresponde con el problema del cálculo del valor futuro de una serie uniforme y periódica de pagos (o ingresos).
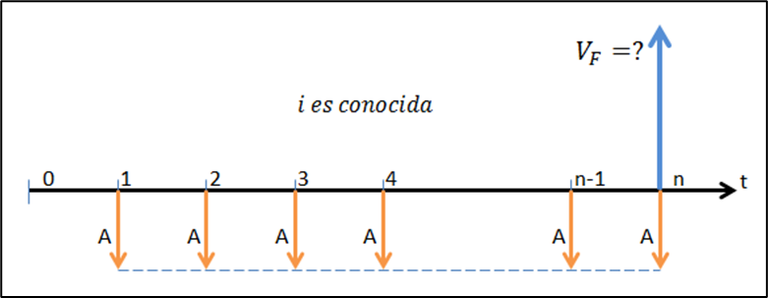
Figura 5.2.
Al sustituir (5.1) en la ecuación que nos permite calcular el valor futuro de un proyecto, se obtiene una fórmula para el valor futuro de la serie uniforme periódica:
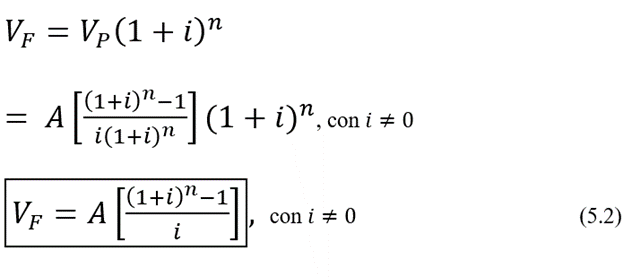
Observa que dados A,n,i puedes obtener el valor final, y que dados el valor final,n,i puedes obtener A. De la figura 5.2 es importante resaltar que el valor futuro que se desea calcular debe siempre estar situado en el mismo período que la última A para que la ecuación (5.2) sea válida.
Ejemplo 5.1 (Tomado y adaptado del Ejemplo 2.3 de Baca (2007))
Se vende una máquina a crédito con las siguientes condiciones: cubrir seis mensualidades iguales de 2.215,170005 USD cada una, que se empezarán a pagar un mes después de hacer la compra. El interés de la compra es del 3% mensual con capitalización mensual. ¿Cuál es el precio de contado?
Solución
Nota que el problema explícitamente indica que el primer pago se efectuará un mes después de la compra, con lo cual se sugiere que la aplicación de la ecuación (5.1) es válida. En consecuencia:
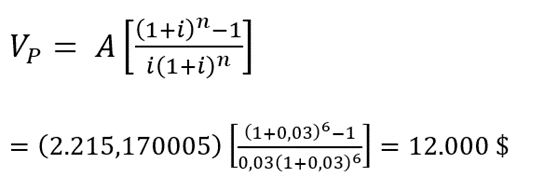
Ejemplo 5.2 (Tomado y adaptado del Ejemplo 2.7 de Baca (2007))
Se depositan 1.000 USD cada mes durante los meses 1 a 6 en un banco que paga un interés de 2% mensual con capitalización mensual. Si no se retira el dinero, ¿cuánto se acumulará en el banco al final del noveno mes?
Solución
El diagrama de flujo de efectivo correspondiente se muestra en la figura 5.3.
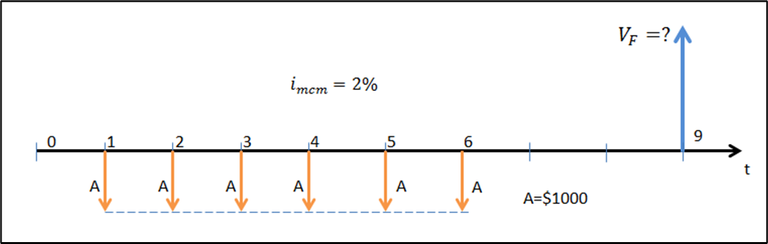
Figura 5.3.
La aplicación de la ecuación (5.2) nos permitirá obtener el valor final de la serie en el mes seis, tal como se explicó antes. Luego de ello, podríamos mover ese valor final al mes nueve con la fórmula de interés compuesto. Veamos:

Referencias
Baca, Gabriel (2007): Fundamentos de Ingeniería Económica. Cuarta edición. Editorial Mc. Graw Hill, México.
Posted Using InLeo Alpha
Posted Using InLeo Alpha
Congratulations @vision4s! You have completed the following achievement on the Hive blockchain And have been rewarded with New badge(s)
Your next target is to reach 1750 upvotes.
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPThank you so much!
That's great @vision4s! You're doing a great job on Hive! We keep cheering you on for your next goal!
BTW, we noticed we miss your support for our proposal. Mays we ask you to check it out and consider supporting it?
All you need to do is to click on the "support" button on this page: https://peakd.com/proposals/248.
Thank you!