
Ahora es el turno de las series de flujos de efectivo que crecen o decrecen aritmética o geométricamente. En este artículo, no entraré en los detalles relativos a la demostración de las ecuaciones; las tomaré como válidas de las referencias que indico al final de este artículo, con el propósito de concentrar esfuerzos en explicar su aplicación. Quien desee corroborar su validez, podrá consultar tales referencias sin problema alguno.
Una serie gradiente es una sucesión de flujos de efectivo que aumenta o disminuye en una cantidad o en un porcentaje constante cada período. Si aumenta o disminuye en una cantidad fija, se denomina gradiente aritmético; si lo hace en un porcentaje fijo, gradiente geométrico.
Series gradiente airtmético
La figura 7.1 ilustra una serie gradiente aritmético que suma una cantidad fija “G” a cada pago del período inmediato anterior. La cantidad “G” se conoce técnicamente como el gradiente aritmético.
Según se observa, los flujos de caja ocurren al final de cada período y la cantidad “G” comienza a sumarse a partir de t = 2, no de t = 1. Además, A, es el valor del primer pago o flujo de caja y ocurre en t = 1.
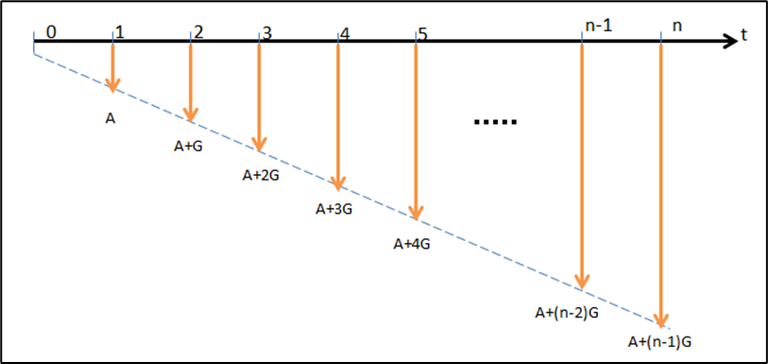
Figura 7.1.
En sentido general, los flujos de caja pueden crecer de forma aritmética (con “G” creciente, positivo) o decrecer de forma aritmética (con “G” decreciente, negativo). En cualquier caso, el enésimo flujo de efectivo valdría:
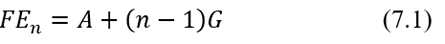
Según lo sugieren la figura 7.1 y la ecuación (7.1), podríamos descomponer la serie en una anualidad con flujos de caja constantes de valor “A” y un gradiente aritmético que inicia en t = 2 y se suma a la magnitud del flujo de caja del período que le antecede, por lo que el valor presente de la serie gradiente aritmético se podría obtener sumando los valores presentes de estas dos componentes. El valor presente de una serie gradiente aritmético es, entonces:
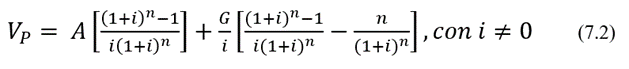
El valor futuro, por su parte, es:
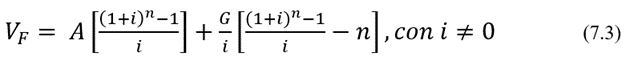
Al aplicar las ecuaciones (7.2) y (7.3) para realizar cálculos, introduciremos el valor de “G” con signo positivo cuando la serie sea creciente y el valor de “G” con signo negativo cuando la serie sea decreciente. Además, i designa la tasa de interés o tasa de descuento.
Series gradiente geométrico
La figura 7.2, por su parte, muestra una serie gradiente geométrico de pagos crecientes. El cambio uniforme de la serie se llama tasa de cambio o gradiente geométrico y suele denotarse con la letra “g”. El valor de “g” puede ser positivo (creciente) o negativo (decreciente). Nótese que el primer pago, A1, ocurre en t = 1 y el gradiente se aplica desde t = 2.
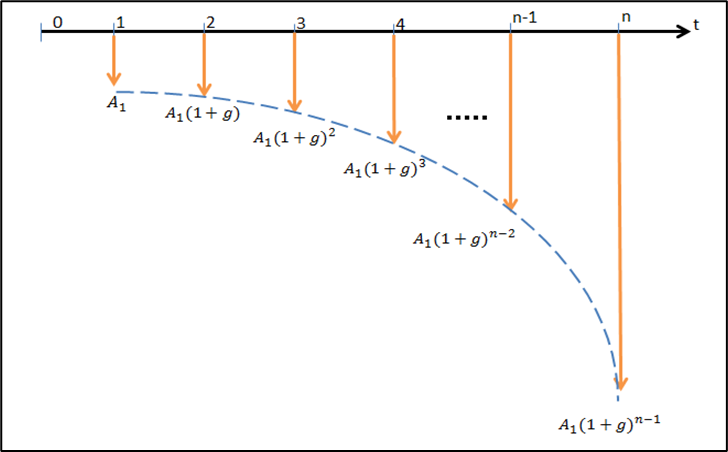
Figura 7.2.
El valor presente de toda la serie gradiente geométrico viene dado por:
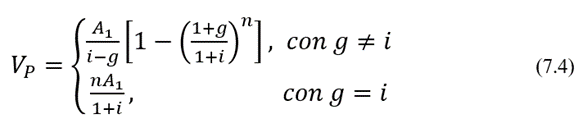
Por otro lado, el valor futuro de la serie gradiente geométrico viene dado por:
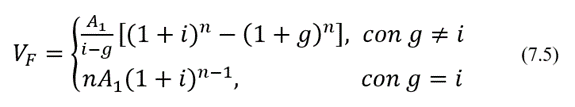
Cuando sustituyamos valores, “g” deberá introducirse con su signo correspondiente en (7.4) y (7.5): positivo si la serie crece y negativo si la serie decrece. En (7.4) y (7.5), i también denota la tasa de interés o tasa de descuento.
Ejemplo 7.1.
¿Cuál será el valor final de un ahorro que se realiza durante 36 semestres iniciando con un pago de 3.000 $ e incrementos semestrales del 4%? La tasa de interés semestral con capitalización semestral es del 3,5%.
Solución
Este escenario representa una serie gradiente geométrico, dado que el incremento fijo es porcentual. En consecuencia, calculamos el valor futuro aplicando la ecuación (7.5) con g diferente de i y con g positivo, porque la serie crece:
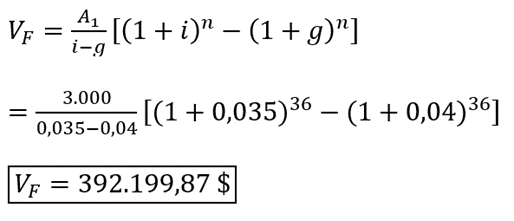
Ejemplo 7.2 (Tomado y adaptado de Garay y González (2007))
Carla está pensando endeudarse para comprar una vivienda. Si la primera cuota del préstamo a 10 años, que debe ser erogada dentro de un año, es de 10.000.000 UM (unidades monetarias) y las cuotas crecen a razón de 5% cada año, ¿cuál es el valor presente de la deuda? La tasa de mercado anual con capitalización anual puede estimarse en 8% durante los próximos 10 años.
Solución
De nuevo, el problema representa una anualidad creciente o serie gradiente geométrico creciente, por lo que podemos aplicar la ecuación (7.4) con g≠i para calcular su valor presente:
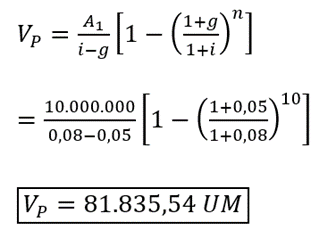
Referencias y complementos
Baca, Gabriel (2007): Fundamentos de Ingeniería Económica. Cuarta edición. Editorial Mc. Graw Hill, México.
Blank, Leland y Tarquin Anthony (2007): Ingeniería Económica. Séptima edición. Editorial Mc. Graw Hill, México.
Garay, Urby y González Maximiliano (2007): Fundamentos de Finanzas con aplicaciones al mercado venezolano. Segunda edición. Ediciones IESA, Caracas.
Posted Using InLeo Alpha