
En esta entrega, presentaré los fundamentos de algunas de las técnicas más usadas en la valoración de proyectos de inversión, desde el punto de vista de la ingeniería económica: la tasa mínima aceptada de retorno (TMAR), el costo promedio ponderado de capital (CPPC), el valor presente neto (VPN) y la tasa interna de retorno (TIR).
Como siempre les comento a mis alumnos, la selección de una alternativa de inversión no se debe basar sólo en el mero cálculo de un indicador, sino en un conjunto de factores que permitan tener una visión mucho más amplia del proyecto.
1. Tasa mínima aceptada de retorno (TMAR)
Todo inversionista debe tener una tasa de rendimiento de referencia sobre la base de la cual hacer sus estimaciones de inversión. Esta tasa es el fundamento de las comparaciones y del cálculo económico que el inversionista realiza.
La tasa mínima aceptada de retorno (TMAR) representa un rendimiento razonable para evaluar y elegir una opción. Un proyecto no es económicamente viable a menos que se espere un rendimiento mayor que la TMAR. La TMAR también recibe el nombre de tasa por superar, tasa de corte, tasa paramétrica y tasa mínima atractiva de rendimiento. Está relacionada con el costo de capital, es decir, con lo que cuesta obtener los fondos requeridos, bien sea con financiamiento por parte de los accionistas o por parte de prestamistas.
Como en todos los países hay inflación, pese a que en algunos pueda ser baja, “ganar en términos reales” significa obtener un rendimiento superior a la tasa de inflación. Si el rendimiento es inferior, se pierde en términos reales porque el poder de compra disminuye; si es igual, el poder de compra se mantiene. En un sentido muy general y sencillo, la TMAR puede calcularse de la siguiente forma, que incluye la inflación de precios:
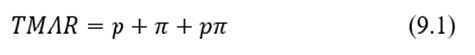
La ecuación (9.1) involucra una prima por riesgo (p) y la tasa de inflación de precios (π). La prima por riesgo es la tasa que cobra el inversionista por arriesgar su dinero en un proyecto de inversión. En la medida en que el proyecto sea más riesgoso, el inversionista exigirá una prima por riesgo mayor.
La TMAR y el costo promedio ponderado de capital (CPPC)
El financiamiento de un proyecto, por lo general, se logra mediante la combinación de capitales provenientes no sólo de los accionistas sino también de prestamistas, instituciones, entre otros.
Para el caso específico de una combinación de fuentes de capital, la TMAR resultante debería ser, como mínimo, el promedio ponderado por aporte de capital de las TMAR de cada fuente (el costo promedio ponderado de capital o CPPC). Así:
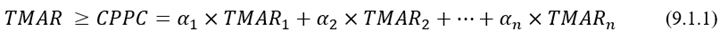
Para (9.1.1) se cumple que:
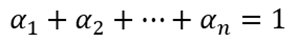
Ejemplo 9.1
Suponga que para un proyecto determinado los accionistas deciden aportar el 50% del capital necesario, una empresa externa el 25% y un banco el otro 25%. La TMAR de cada uno de ellos es 45%, 39% y 26% respectivamente. ¿Cuál será la TMAR mínima aceptable?
Solución
La TMAR mínima resultante será el costo promedio ponderado de capital:
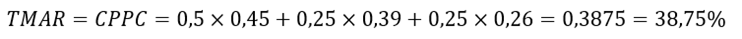
Es decir, en promedio, lo que las fuentes de capital particulares del proyecto aceptarán como tasa mínima de rendimiento es un 38,75% sobre la inversión.
2. Período de recuperación del capital (PRC)
Es el lapso (generalmente medido en años) que tomará un proyecto para recuperar la inversión inicial. En general, es una técnica poco usada porque no toma en cuenta el valor del dinero en el tiempo ni tampoco involucra todos los flujos de efectivo.
Considere los datos de la tabla 9.1. En ella se muestran los flujos de caja de dos proyectos mutuamente excluyentes para un horizonte de planeación de seis años. Según la técnica PRC, el proyecto A debería ser el escogido porque permite recuperar el capital inicial invertido (-500) en tan solo dos años, mientras que el B lo hace en 3,5 años.
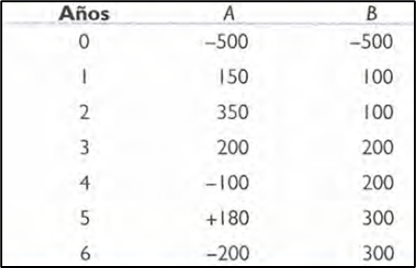
Tabla 9.1.
Sin embargo, Si tomáramos en cuenta todo el horizonte de planeación (los 6 años), el proyecto B sería claramente superior.
Existe también un método más amplio en alcance denominado período de recuperación del capital descontado (Véase Garay y González, 2007), pero no lo abordaré en esta entrega.
3. Valor presente neto (VPN)
Es el valor presente de una serie de flujos netos de efectivo que incluye la inversión inicial (Io). Esto se escribe matemáticamente como la siguiente suma algebraica:
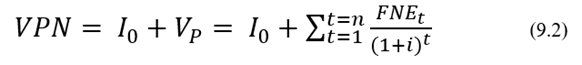
Por convención, a los egresos se les asigna un signo negativo y a los ingresos uno positivo en esta sumatoria. En la ecuación (9.2), FNEt denota el flujo neto de efectivo en el momento t; i, la tasa de descuento, que debería ser como mínimo la TMAR; Io, la inversión inicial; y n, el número de períodos para el cálculo del VPN.
Al VPN se le suele llamar también valor actual neto (VAN). Ya nos familiarizamos algo con él en el artículo anterior, cuando estudiamos la técnica del CAUE.
Criterio basado en el VPN para seleccionar entre alternativas con vidas iguales
La siguiente regla aplica para la toma de decisiones:
Para sólo una alternativa de inversión: Si VPN > 0, se acomete, dado que el proyecto agregará valor (aumentará la riqueza de los inversionistas); si VPN < 0, no se acomete porque restará valor; si VPN = 0, la decisión de acometer o no acometer no implicará ganancia o pérdida de valor. En la práctica, ninguna inversión se emprende sólo sobre la base de un análisis de VPN; el análisis debe extenderse, pero un VPN positivo es un primer buen indicador.
Para dos o más alternativas: escoja aquella que procure el mayor VPN, es decir, el VPN menos negativo o el VPN más positivo.
Ejemplo 9.2 (Tomado y adaptado de Blank y Tarquin (2007))
Cierto laboratorio de una universidad es contratista de la NASA para sistemas espaciales de celdas de combustible a base de hidrógeno y metanol. Durante las investigaciones, surgió la necesidad de evaluar la economía de tres máquinas de igual servicio. Si la TMAR es de 10% anual, ¿cuál máquina debería escoger?

Tabla 9.2.
Solución
Para determinar cuál de las alternativas con vida útil igual es la más apropiada, apliquemos la ecuación (9.2):
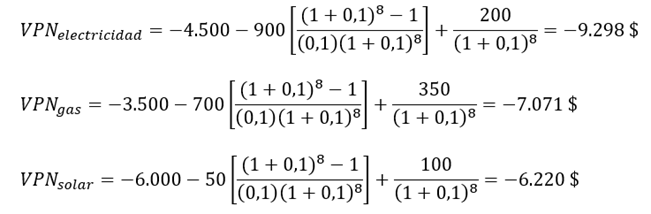
Según el criterio, se debe escoger la alternativa de la energía solar por tener el mayor VPN en términos numéricos, es decir, el VPN menos negativo.
Criterio basado en el VPN para seleccionar entre alternativas con vidas diferentes
Las alternativas deben terminar al mismo tiempo para poder compararlas apropiadamente. Sobre la base de la misma directriz aplicada para opciones con iguales vidas, se aplica cualquiera de las siguientes reglas prácticas:
i) MCM: se compara el VPN de las alternativas durante un período igual al mínimo común múltiplo (mcm) de sus vidas estimadas.
ii) Horizonte de planeación: se compara el VPN de las alternativas empleando un número de años específico, que no necesariamente tiene que ver con la vida útil de una opción en particular.
El enfoque MCM hace que los flujos de efectivo se extiendan el mismo período para todas las alternativas de forma automática. Para poder aplicarlo, se requiere que las siguientes tres premisas se cumplan:
i) El servicio ofrecido por las opciones será necesario durante un número de años igual al MCM o más.
ii) La alternativa seleccionada se repetirá durante cada ciclo de vida dentro del MCM exactamente en la misma forma.
iii) Los estimados del flujo de efectivo serán los mismos en cada ciclo de vida.
Con este enfoque, el primer costo de una alternativa se reinvierte al inicio de cada ciclo de vida y el valor de rescate estimado se considera al final de cada ciclo de vida también.
Por otro lado, el enfoque del horizonte de planeación será requerido si la primera de las tres premisas anteriores no se cumple. Para aplicarlo, se elige un número de años (o períodos) durante el cual se realiza el análisis económico. Se ignoran todos los flujos de efectivo que ocurran más allá de tal horizonte. Se considera un valor de mercado estimado al final de ese período.
El horizonte de planeación escogido debe ser relativamente corto y útil cuando el enfoque MCM genera un período de evaluación muy largo. Por ejemplo, suponga que tiene dos alternativas mutuamente excluyentes de 5 y 9 años de vida. Si aplica el método MCM, tendrá que basar su estudio en un período de 45 años (dado que mcm(5, 9) = 45). Un estudio que se extendiera por 45 años, sería inconveniente e irreal, por lo que en este caso se debería abordar el problema desde la óptica del horizonte de planeación.
Ejemplo 9.3 (Tomado y adaptado de Blank y Tarquin (2007))
La empresa National Hombuilder planea comprar nuevo equipo de corte y terminado. Dos fabricantes ofrecen las cotizaciones siguientes:

Tabla 9.3.
a) Determine qué fabricante debe seleccionarse con base en la comparación del valor presente, si la TMAR es de 15% anual.
b) La empresa tiene una práctica estandarizada de evaluación para todos sus proyectos de un periodo de cinco años. Si se utiliza el periodo de estudio de cinco años y no se espera que varíe el valor de rescate, ¿qué fabricante debe seleccionarse?
Solución
a) Como los dos equipos poseen vidas distintas, se aplica el método MCM en primera instancia. El mínimo común múltiplo entre 6 y 9 años es 18 años. En consecuencia, tal y como lo exige el enfoque MCM, habrá que considerar tres ciclos de vida para el fabricante A (de 6 años cada uno) y dos para el fabricante B (de 9 años cada uno). Para el fabricante A, además, el segundo ciclo de vida comenzará en el año 6, cuando termina el primero; el tercero comenzará en el año 12. Para el fabricante B, el segundo ciclo de vida iniciará en el año 9, cuando termina el primero para él. El diagrama de flujo de efectivo general se muestra a continuación.
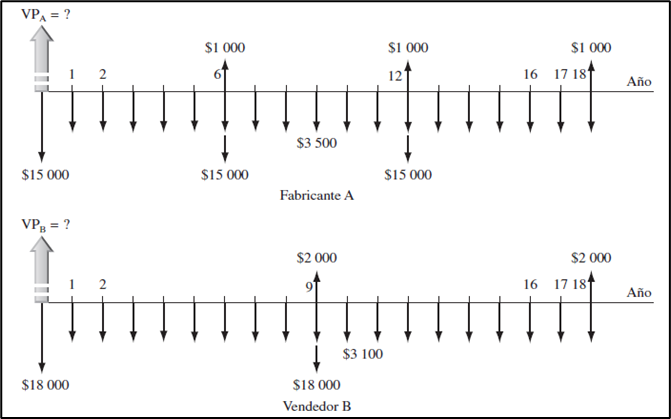
Figura 9.1.
Entonces:

Se escoge el fabricante B por tener el VPN mayor en términos numéricos (el menos negativo).
b) Ahora, el horizonte de planeación se reduce a cinco años. Por tanto, el valor de rescate de cada alternativa ocurre en t = 5 y, además, no varía según el enunciado del problema.
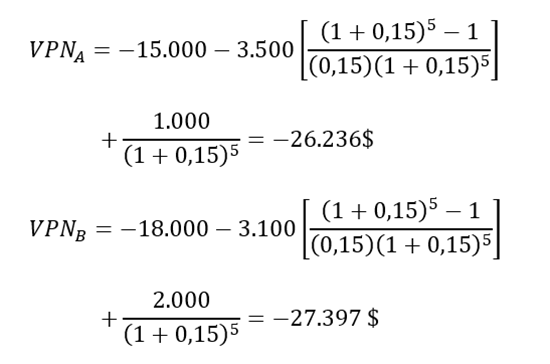
Sobre la base de este criterio, se debería escoger al fabricante A. El período de estudio más corto provocó un cambio en la decisión económica.
4. Tasa interna de retorno (TIR)
Es la tasa de descuento que hace que el VPN del proyecto sea cero; en otras palabras, a esta tasa de descuento, el valor presente de los flujos netos de efectivo (FNE) durante la vida del proyecto igualará el monto de la inversión inicial.
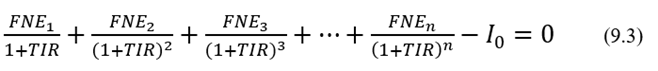
La resolución de la ecuación (9.3) para la variable TIR nos proporciona la tasa interna de retorno del proyecto. Es evidente que con más de dos términos, la obtención de una solución para (9.3) se complica y se hace necesario echar mano de técnicas numéricas para tal fin. Sin embargo, las calculadoras financieras y los paquetes como Excel, Matlab, Python y R nos facilitan la vida.
Una definición alterna para la TIR (Baca, 2007) es que se trata de la tasa de interés que iguala el valor futuro de la inversión con la suma de los valores futuros equivalentes de los flujos netos de efectivo, al comparar el dinero al final del período de análisis.
Criterio basado en TIR para seleccionar una alternativa
Si la TIR es mayor o igual que la TMAR, el proyecto debe acometerse; si la TIR es menor que la TMAR, se debe rechazar.
Dicho de otra forma, si el rendimiento que genera el proyecto por sí mismo es mayor (o como mínimo igual) que la tasa de ganancia mínima que solicitan los inversionistas (TMAR), la inversión es económicamente viable.
¿Tiene sentido una TIR negativa?
En general, una TIR que resulte negativa sugiere que la inversión es superior a los flujos de caja netos descontados del proyecto. Dicho de otra forma, una TIR negativa indica que el valor presente de las erogaciones supera el valor presente de los ingresos. En un caso de esta naturaleza, no es necesario comparar la TIR con la TMAR (o con la tasa de descuento).
Desde un punto de vista matemático, el valor de la TIR puede oscilar entre -100% e infinito. En términos de inversión, una TIR = -100% implica que se perdió por completo la inversión.
Desventajas del uso de la TIR
Tanto la TIR como el VPN suponen que todas las ganancias anuales (flujos netos de efectivo) se reinvierten en la propia empresa por completo, lo cual –en la práctica– podría ocurrir en algunos años, pero no en todos. Si un año determinado se reparten dividendos, por ejemplo, ya no es posible alcanzar la TIR predicha por el cálculo inicial. El nombre de tasa interna de retorno deriva precisamente del hecho de suponer que es un rendimiento generado sólo por la reinversión de todos los flujos netos de efectivo en el propio proyecto.
El cálculo de la TIR supone resolver un polinomio de grado n. La regla de los signos de Descartes indica el número de raíces distintas del polinomio: “Un polinomio puede tener tantas raíces reales como cambios de signo tenga”. Un polinomio con dos cambios de signo implica un polinomio con, a lo sumo, dos raíces útiles, y en nuestro caso particular dos TIR aparentes, lo cual no tiene una interpretación económica. Lo mismo ocurre con más cambios de signo. Cuando se da este tipo de casos, la TIR por sí sola no es útil para tomar decisiones y se debe ampliar el análisis aplicando técnicas adicionales.
Flujo de efectivo convencional
Si los signos algebraicos de los flujos de efectivo sólo cambian una vez, estamos en presencia de un flujo de efectivo convencional. Aunque no es el único escenario de convencionalidad, es muy común que los signos cambien de negativo a positivo en el año cero (porque en t = 0 se eroga la inversión inicial y luego los flujos suelen ser ingresos netos). Cuando los signos cambian más de una vez durante la vida del proyecto, se dice que el flujo de efectivo es no convencional.
Es muy importante tener en cuenta que al decidir respecto de invertir o no en un proyecto, los métodos VPN y TIR conducen al mismo resultado, por lo general (son equivalentes), pero cuando se comparan dos o más proyectos podrían ocurrir contradicciones. En estos casos, es recomendable usar el VPN y no la TIR (Baca, 2007).
¿Qué hacer cuando obtenemos varias tasas de rendimiento al resolver para la TIR?
Debemos proceder a eliminar algunas de las tasas obtenidas con base en un análisis adicional.
“El resultado del análisis para obtener un solo valor cuando existen varios valores de la tasa de rendimiento que no son útiles no determina la tasa interna de rendimiento (TIR) de una serie de flujo de efectivo no convencional. La tasa resultante es función de información adicional que se provee para que la técnica seleccionada funcione, por lo que la exactitud depende de la confiabilidad de dicha información.” (Blank y Tarquin, 2007)
La tasa a la que se refieren estos autores se llama tasa externa de retorno (TER), es decir, una tasa que no se obtiene dentro del proyecto a la que se invierten los flujos de efectivo. Existen, en esencia, dos métodos para eliminar múltiples raíces de la tasa de rendimiento: el enfoque TRM (tasa de rendimiento modificada) y el enfoque RSCI (rendimiento sobre capital invertido). Ilustraré sólo el primero en este artículo.
Enfoque TRM: Procedimiento
1°. Se traen a valor presente (VPo) todos los flujos de efectivo negativos con una tasa externa que es la requerida para obtener fondos adicionales para el proyecto, llamada tasa de préstamo ib. Es razonable usar como valor el costo promedio ponderado de capital o CPPC.
2°. Se llevan al final del horizonte de planeación (VFn) todos los flujos de caja positivos a una tasa externa a la que se invierten, llamada tasa de inversión ii. Es razonable usar la TMAR en este caso.
3°. Para obtener una sola tasa de retorno, se despeja i’ de la siguiente ecuación que considera los valores VPo y VFn descritos en los dos puntos previos:
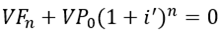
4°. El proyecto se justifica económicamente si i’ = TER > TMAR; en caso contrario, no.
Veamos un ejemplo de aplicación.
Ejemplo 9.4 (Tomado y adaptado de Blank y Tarquin (2007))
Una empresa tiene los siguientes flujos de efectivo:
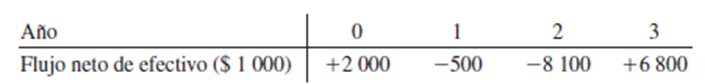
Ya se han determinado las raíces del polinomio y dos satisfacen la ecuación de VPN: 7,47% y 41,35% anual. Obtenga el valor de la TER usando el enfoque TRM. El CPPC de la empresa es de 8,5% anual, y tenga en cuenta que se rechazan los proyectos con un retorno inferior al 9%. Se espera que cualquier excedente de fondos generados obtenga un 12% anual.
Solución
De la tabla, vemos que n = 3. Además, de los datos proporcionados, concluimos que:

Luego:
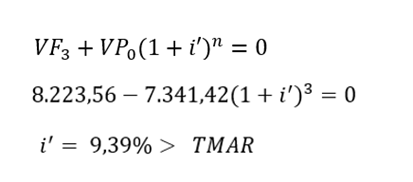
¡El proyecto sí se justifica!
Al comparar dos o más alternativas sobre la base de la tasa de rendimiento, o de la TIR si es el caso, se suele aplicar una técnica que se llama análisis incremental. Recomiendo su posterior estudio.
Referencias y complementos
Baca, Gabriel (2007): Fundamentos de Ingeniería Económica. Cuarta edición. Editorial Mc. Graw Hill, México.
Blank, Leland y Tarquin Anthony (2007): Ingeniería Económica. Séptima edición. Editorial Mc. Graw Hill, México.
Garay, Urby y González Maximiliano (2007): Fundamentos de finanzas con aplicaciones al mercado venezolano. Segunda edición. Ediciones IESA, Caracas.
Posted Using InLeo Alpha
Excelente 👏🏻