Es normal que el financiamiento de un proyecto se logre con una combinación de capital propio, proveniente de los accionistas, y préstamos, provenientes de acreedores. En entornos de mayor libertad económica, los mercados de capitales suelen ser más desarrollados y muchas empresas, las que cumplen con una serie de requerimientos, pueden acudir a ellos para levantar los fondos necesarios para sus acometidas (mediante, por ejemplo, la emisión de bonos o de acciones). Sin embargo, en economías como la nuestra, o en aquellas economías más desarrolladas, pero para empresas que no tienen la opción de volcarse a los mercados de capitales, la fuente de financiamiento principal radica en los créditos bancarios.
La empresa que obtiene un crédito debe entonces “servir” la deuda, es decir, honrar los pagos periódicos previamente establecidos en el contrato subyacente. Los analistas deben tomar en consideración ese servicio de la deuda en sus cálculos porque ello, sin duda, impacta la rentabilidad y la viabilidad de los proyectos.
Aunque pueden existir múltiples opciones disponibles, es común encontrarse en la práctica con tres sistemas de crédito o sistemas de amortización: a) el sistema francés; b) el sistema alemán; y c) el sistema americano. Presentaré en este artículo los fundamentos de cada uno de ellos.
1. Sistema francés
Se caracteriza por ser de cuotas constantes. En otras palabras, los pagos periódicos que se realizan para honrar la deuda son siempre de la misma magnitud. Cada uno de esos pagos contiene un componente de intereses, que se aplica sobre el capital pendiente por pagar en cada período, y un componente de amortización, que se resta del capital pendiente en cada período. Es lógico suponer entonces que los intereses y la amortización variarán a lo largo de la vida de la deuda, compensando entre sí tales variaciones, de tal forma que las cuotas permanezcan constantes.
Como en un principio se adeuda todo el capital, los intereses sobre el saldo pendiente se corresponderán con una fracción mayor de la cuota, mientras que lo que se amortiza (o abona a capital) con una menor. Conforme el tiempo avance, la amortización aumentará (geométricamente) y los intereses disminuirán, hasta que se extinga por completo la deuda. Por ello, este sistema también se llama sistema de amortización progresiva (ver Figura 10.1).
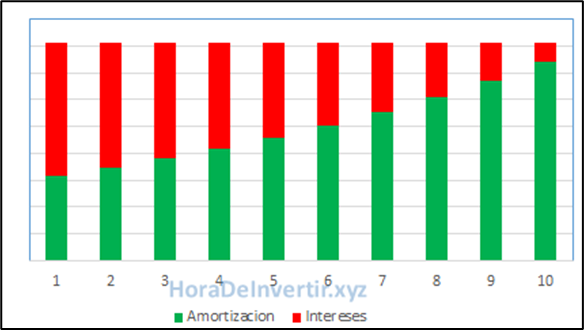
FIgura 10.1. Sistema francés.
En este contexto, el término amortización se refiere al reintegro de los fondos prestados en un tiempo preestablecido.
Cuota periódica
La cuota periódica pura se calculará con la ecuación (10.1), que no es más que la ecuación del valor presente de una serie uniforme con “A” despejada:
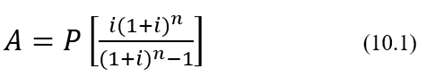
“P” es la cantidad recibida en préstamo (el principal); “i” es la tasa de interés que le cobrará la institución o el tercero por el préstamo; “n” es el número de períodos que transcurren desde el momento en que se recibe el préstamo hasta el momento en que se extingue la deuda; y “A” es la cuota periódica constante.
Intereses
Siempre se aplican sobre el saldo deudor:
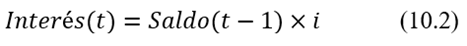
En (10.2), Saldo(t-1) es el saldo del período inmediatamente anterior al actual e Interés(t) es el monto por intereses, en unidades monetarias, que se paga en el momento presente. Es evidente que para el período t = 1, el saldo es el monto total del préstamo, dado que aún no se ha amortizado nada.
Amortización
Es el pago a principal que se realiza en cada período.
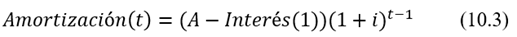
En (10.3), Interés(1) es el monto de los intereses pagados en t = 1 y Amortización(t) es el monto amortizado en el momento presente. La amortización también se puede calcular de la siguiente forma:
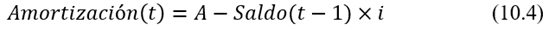
Saldo deudor
Es el saldo que queda pendiente en cada período, luego de la amortización correspondiente.
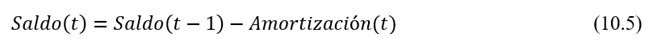
Ejemplo 10.1
Supongamos que un prestamista le otorga en crédito a cuatro años por 1.000 USD para comprar un equipo específico. Él le cobrará un interés compuesto anual de 10%. ¿Cuál será el valor de la cuota constante que deberá pagar durante esos cuatro años para cancelar la deuda? Muestre una tabla de amortización de la deuda.
Solución
Aplicando la ecuación (10.1), encontramos el valor de la cuota periódica constante:
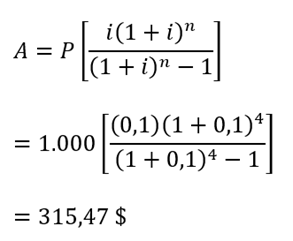
En otras palabras, para cancelar el crédito, usted tendrá que pagar al finalizar cada año 315,47 $ durante 4 años. Ahora bien, construyamos una tabla para analizar la evolución de la deuda durante su tiempo de vida:
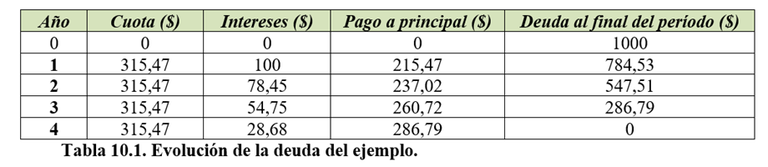
En la tabla anterior, observamos que el monto que aparece en la columna Intereses se obtiene multiplicando la tasa de interés (10%) por el monto que aparece en Deuda al final del período correspondiente al período anterior. El monto que aparece en la columna Intereses se resta de la cuota fija para obtener así el Pago a principal (amortización). De la Deuda al final del período anterior se resta el Pago a principal para obtener, a su vez, la Deuda al final del período actual.
Con la lógica descrita en el párrafo anterior, se procede a llenar la tabla hasta que la deuda se haya cancelado por completo. Año tras año, el pago de intereses y el pago a principal afectarán sus flujos netos de efectivo. He allí la importancia de considerarlos. Este hilo lógico es el mismo que podemos emplear para crear una hoja Excel, o un sencillo programa, que automatice los cálculos.
Importante: el interés formará parte de los costos financieros que se usan para calcular la utilidad antes de impuestos. El interés sirve como “escudo fiscal” porque permite reducir la utilidad, con lo que se disminuye el impuesto que se paga. El pago a principal, por su parte, no se deduce de impuestos, pero sí debe ser restado de la utilidad neta para obtener los flujos netos de efectivo anuales de sus proyectos dado que es, en efecto, un desembolso de dinero.
2. Sistema alemán
Se caracteriza por ser de amortización constante, lo cual hace que las cuotas periódicas decrezcan, puesto que los intereses sobre el saldo deudor son cada vez menores (cada vez se debe menos hasta extinguir la deuda). En seguida, tal como hice con los parámetros relevantes del sistema anterior, presento las ecuaciones para calcular la amortización, la deuda cancelada, el saldo deudor, los intereses y la cuota periódica.
Amortización
En este caso, se calcula así:

En (10.6), “P” es el monto total del préstamo y “n” el número de cuotas.
Deuda cancelada (DC)
Se calcula de la siguiente forma:
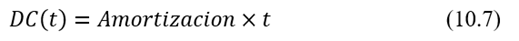
Saldo deudor
La ecuación (10.8) nos indica cómo determinarlo:

Intereses
Se calculan sobre el saldo del período anterior:
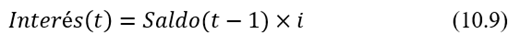
Cuota periódica
Finalmente, la cuota periódica en este caso viene dada por:
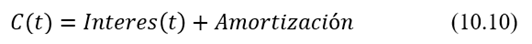
La figura 10.2 ilustra cómo variarían las cuotas con este sistema de crédito.
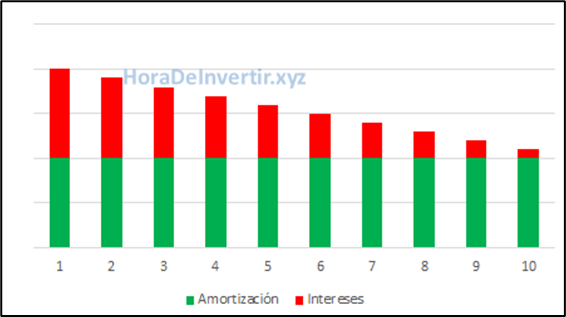
Figura 10.2. Sistema alemán
Ejemplo 10.2
Un banco le otorga en crédito a cuatro años de 100.000 € para adquirir una nueva tecnología. Le cobrará un interés compuesto anual de 10%, según sistema de amortización constante. Muestre una tabla de evolución de la deuda.
Solución
Determinemos la amortización que ocurrirá al final de cada período:
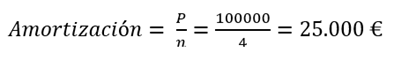
Las cifras de la tabla siguiente están expresadas en euros.
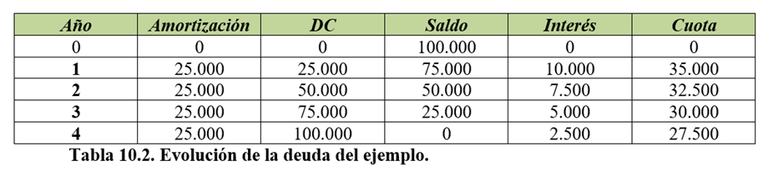
La tabla se llenó haciendo uso de las ecuaciones (10.6) a (10.10) para los períodos apropiados.
3. Sistema americano (sistema de dos tasas)
Se caracteriza por el hecho de que el préstamo se amortiza por completo al final del contrato. A lo largo de éste, sólo se pagan intereses, tal como se ilustra en la Figura 10.3.
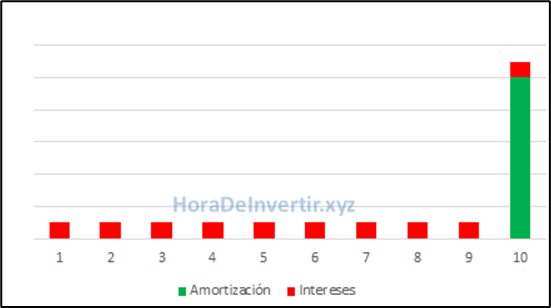
Figura 10.3. Sistema americano.
Los parámetros de relevancia para este sistema se calculan con las ecuaciones que se detallan a continuación.
Cuota periódica
Desde el período 1 hasta el período “n-1”:
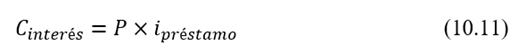
En el período “n” la cuota contendrá el principal también: 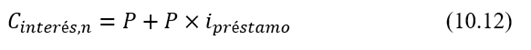
Amortización
La amortización es cero durante toda la vida del contrato, excepto en el último período, cuando se amortiza por completo.
Saldo deudor
El saldo deudor es siempre el monto total del préstamo hasta que ocurre el último pago, momento en el cual el saldo deudor se anula.
Opción especial: fondo de amortización
Por lo general, en paralelo, se abre una cuenta de caja de ahorro con el objeto de acumular el monto necesario para cancelar la deuda y no tener que pagar todo el principal al final, pero esto es optativo.
Si se decide emprender esta opción, a la cuota periódica que se paga por el préstamo, se suma una cuota periódica de amortización. Tal cuota periódica de amortización se calcula a partir de la ecuación del valor futuro de una serie uniforme, donde el valor futuro es precisamente “P”, que es lo que se debe tener disponible en la caja de ahorro en el período “n”:

Amortización acumulada en el fondo (Aa)
Para calcularla, aplicamos (10.15):
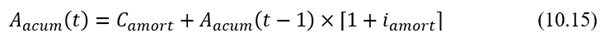
Saldo deudor en el fondo de amortización
Lo determinamos aplicando (10.16):
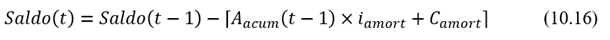
Si se opta por el fondo, las cuotas siempre vendrán dadas por (10.14), desde t = 1 hasta t = n inclusive.
Ejemplo 10.3
Un banco le otorga en crédito a cuatro años de 100.000 € para ampliar su planta. Le cobrará un interés compuesto anual de 10%, según sistema americano. Usted decide optar por un fondo de amortización para no tener que devolver todo el principal al final de los cuatro años. El interés que devengarán sus aportes en ese fondo es de 5%. Muestre una tabla de evolución de la deuda.
Solución
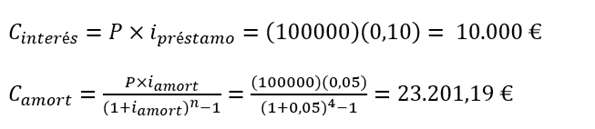
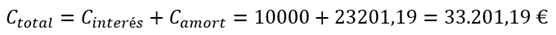
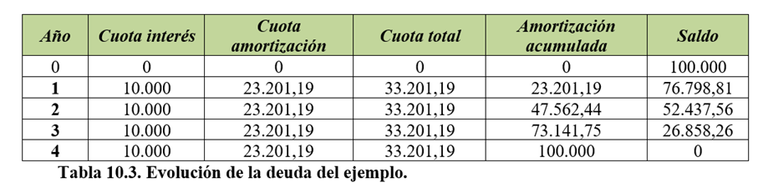
Las ecuaciones (10.13) a (10.16) fueron empleadas para llenar la tabla que se muestra a continuación. Los montos están expresados en euros.
Referencias y complementos
Bacchini, Roberto y otros (2008): Modelos Financieros Utilizando Microsoft Excel. Primera edición. Editorial Omicron, Argentina.
Silva, Jesús (1993): Fundamentos de Matemática Financiera. Edición corregida. Editorial CO-BO, Caracas.
Posted Using InLeo Alpha
