Introduction
In this post I explore implementing a probabilistic method to ensure that a fixed number of rare events occur within a predetermined number of trials.
The example I have in mind is guaranteeing the distribution of a fixed number of rare trading cards in booster packs, where the total number of packs is also fixed. So if I have 2 rare cards to distribute in 600 packs, how do I make sure that
the distribution method is random and fair
all the rare cards are found
ChatGPT proposed solution
I started with prompts in ChatGPT to try and find out if there are any well-known, established methods and algorithms for this purpose. This was the prompt I used:
"Are there established algorithms that make sure a fixed number of random rare events always happen in a maximum predetermined number of rolls?"
After some refinement, ChatGPT came up with what I consider three valid approaches
The positions of the rare events are predetermined but unknown to the public, so they appear to be random.
The probability of finding a rare event starts at the baseline value (where every event has the same probability) and increases progressively until a rare event occurs. This increase will reach a point where occurrences are guaranteed.
Same as the previous point, but with checkpoints. So using the initial 2 in 600 example would mean 1 of the rare cards would be found before the 300th booster pack and the other between the 301st and the 600th booster.
Method 1 is not transparent and the randomness is only apparent. The predetermined allocation may follow criteria that are not fair and could be manipulated, reducing trust. It also requires hardcoding the positions of the rare events and would need to be modified for each execution. This potentially creates more opportunities for mistakes.
Methods 2 and 3 can be implemented with reusable code that allows for multiple executions without modifications. I asked ChatGPT for an implementation of the algorithm in Javascript for method 2. Afterwards I made modifications that allow switching between methods 2 and 3 easily. This is the code ChatGPT generated:
function dynamicProbabilityDistribution(totalTrials, totalRareEvents) {
// Initialize remaining counts of trials and rare events
let remainingTrials = totalTrials;
let remainingRareEvents = totalRareEvents;
// Array to store the result of each trial
const results = Array(totalTrials).fill("common");
// Loop over each trial
for (let i = 0; i < totalTrials; i++) {
// Calculate the probability of a rare event for the current trial
const probabilityOfRare = 1 - (1 - remainingRareEvents / remainingTrials);
// Randomly determine if the current trial yields a rare item
if (Math.random() < probabilityOfRare) {
results[i] = "rare";
remainingRareEvents--; // Decrease rare event count if one is found
}
// Decrease the number of remaining trials
remainingTrials--;
// Stop early if all rare events have been distributed
if (remainingRareEvents === 0) {
break;
}
}
// If any rare events remain undrawn by the last few trials,
// fill those in the remaining trials to ensure all rare events are distributed
let j = totalTrials - 1;
while (remainingRareEvents > 0) {
if (results[j] === "common") {
results[j] = "rare";
remainingRareEvents--;
}
j--;
}
return results;
}
// Example usage
const totalTrials = 10000;
const totalRareEvents = 100;
const results = dynamicProbabilityDistribution(totalTrials, totalRareEvents);
console.log(results);
Click here for color-coded Gist
I think ChatGPT hallucinated a little bit at the end, but the core principle seemed sound.
So I used this example as a starting point and made some improvements.
My implementation
I introduced the following modifications:
Removed the superfluous check at the end of the function;
Modified the reporting to the console;
Recorded the results in a CSV file.
Introduced an extra loop to repeat the execution of the algorithm for testing purposes (simulate multiple iterations). This feature could also be used as the implementation of the checkpoint method mentioned previously.
You can easily change the variables to create evenly distributed checkpoints - method 3 (where each rare event is guaranteed to occur every x trials). The number of checkpoints is never used, but it would be the number of rare events - 1. The changes are:
Set
totalTrialsto the size of the 'blocks', i.e., the maximum number of trials divided by the number of rare events. If you want to have 1 checkpoint so that 1 rare event occurs in each half of the maximum number of 600 trials, set this variable to 300.Set
totalRareEventsto 1 (so that only one rare event happens between each checkpoint);Set
simulvariable to indicate the number of rare events. This effectively encapsulates finding each rare event in its own RNG loop.
The variable completedTrials is unnecessary for execution and was put in place only to confirm whether the actual number of trials ever surpassed the established limit.
import * as fs from 'fs';
const dynamicProbabilityDistribution = (totalTrials, totalRareEvents) => {
// Initialize counters
let remainingTrials = totalTrials;
let remainingRareEvents = totalRareEvents;
let foundRareEvents = 0;
let completedTrials = 0;
// Loop over each trial
for (let i = 0; i < totalTrials; i++) {
// Calculate the probability of a rare event for the current trial
const probabilityOfRare = 1 - (1 - remainingRareEvents / remainingTrials);
// Randomly determine if the current trial yields a rare item
if (Math.random() < probabilityOfRare) {
foundRareEvents ++;
remainingRareEvents--; // Decrease rare event count if one is found
dataCSV += `${i+1},`;
console.log("Trial #", i+1, "found rare event #", foundRareEvents);
}
// Update counters
remainingTrials--;
completedTrials++;
// Stop early if all rare events have been found
if (remainingRareEvents === 0) {
console.log("All rare events found after", i+1, "trials");
break;
}
}
dataCSV += `${completedTrials}\n`;
console.log("Completed trials:", completedTrials);
}
// START HERE
const totalTrials = 600;
const totalRareEvents = 2;
const simul = 10000; // Simulate multiple executions / iterations OR create checkpoints
// Reset the .csv results file and write the header
var dataCSV = "";
const pathCSV = './trial_results.csv';
const eventLabels = Array.from({ length: totalRareEvents }, (_, i) => `Event_${i + 1}`).join(',');
fs.writeFile(pathCSV, `Iteration,${eventLabels},Max_trials\n`, (error) => {
if (error) throw error;
});
// Simulate multiple runs / use checkpoints
for (let j = 0; j < simul; j++) {
const iter = j+1;
console.log("Simulation run #", iter);
dataCSV += `${iter},`;
dynamicProbabilityDistribution(totalTrials, totalRareEvents);
}
// Sava data to file
fs.appendFile(pathCSV, dataCSV, (error) => {
if (error) throw error;
});
Click here for color-coded Gist
Analysis of the results
I wanted to see if the results over many executions of the script would yield skewed results or if the execution would fail the basic premises. So I ran the script 10,000 times with the parameters of finding 2 rare events in 600 trials. I wanted to check if
The 2 rare events were always found each time
The 2 rare events were always found within 600 trials
The distribution of the winning trials was random and not skewed or clumped around certain value ranges
How many times the last rare event was found on the last trial
How many times both rare events were found 'too early'
I imported the CSV file into Google Sheets. A did some simple data analysis and plotted the data in a few graphics. I didn't run any statistical tests for randomness, I don't think that extra work would add much to what the graphs already show.
Here are my main takeaways, after running the algorithm 10,0000 times:
All the rare events were found within the established limit;
The last rare event was 'forced' into the last trial 36 times;
The median - the 'typical' number of trials necessary to find all rare events - was 424;
The rare events appear to be randomly distributed. A scatter plot does not reveal any obvious skewing or clumping;
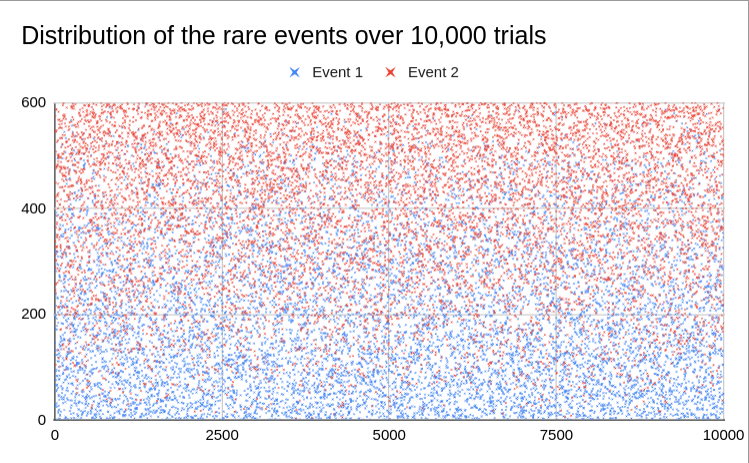
As expected, occurrences of the first event are concentrated in the bottom half while the second event happens mostly in the top half;
All rare events happened within the first 200 trials (1/3), i.e., 'too early', 1122 times (11.22%);
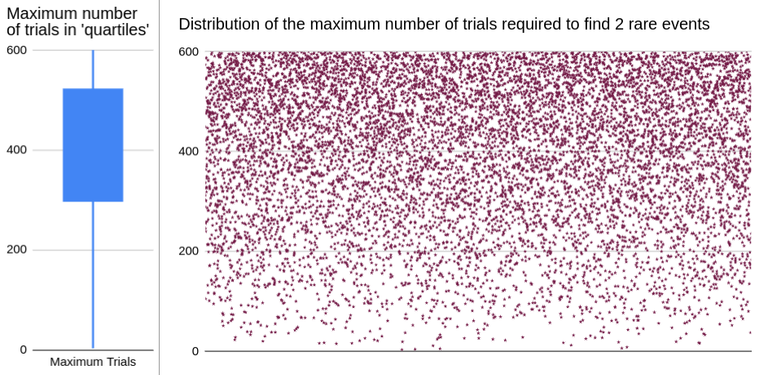
The maximum number of trials required to find all rare events skews towards the end, as expected. There are still plenty of runs that end prematurely, as seen below;
25% of the runs end before about half (298) of the total possible trials are calculated;
50% of the runs end after about 2/3 (424) of the trials are calculated. This means half the time the 'suspense' of finding all the rare events goes into the final third of the possibility space;
My conclusions
This algorithm appears to correctly distribute random events within a fixed number of trials, without leaving any rare events unfound, as desired.
Although the distribution appears to be fair and random, trials at the very start or right after a rare event occurs will have slightly unfavorable odds, but never under the baseline odds where every rare event would have the same odds. This also means that in situations where rare events occur very late, the odds for each will be much better than at the start.
The constraints of this example - just 2 rare events in 600 - result in a number of occurrences where all the rare events could be found very quickly. This may not be ideal in situations where creating ongoing suspense and motivation to participate is desirable.
The checkpoint solution solves this issue, but could also create distortions in the behavior of participants, as could find the pattern where after each rare event occurs, the odds for the next one would be zero until the checkpoint is reached. The upside is a guarantee that the incentives to engage are spread more evenly across the total number of trials.
So none of these solutions actually create an ideal scenario where the interest in finding one of those rare events is maintained evenly until the end of the trials. These solutions play on the excitement of finding a rare event while the trials are still ongoing, but if all the rare events are found prematurely or unevenly (when using checkpoints) this excitement can turn into resentment, frustration or apathy in reaching the end of the trials (i.e., buying all boosters). The extra incentive in the form of rare and valuable rewards could become a source of dissatisfaction.
Then there is also the case where not all trials are executed. In my example that would correspond to not all boosters being opened or purchased. In this situation, it is legitimate to expect that not all rare events / cards would be found. What to do in this case, if it is desirable that all rare events should occur? The algorithm solution I present does not offer a solution in this case.
An alternative approach (from a game perspective) would be to determine the winners of those rare events at the end, after all trials have been completed - in other words, a raffle. This would make all events equally valuable during the acquisition period, maintaining a constant, positive pressure to reach the end - all trials would have strictly the same odds of being awarded a rare event. A raffle can also distribute all rare events irrespective of whether all the trials are completed or not - the rare events are calculated within the range of the trials that actually happened (i.e., the boosters that were purchased).
While the algorithm I present here tests the odds at every single trial, a raffle randomly picks numbers from an existing pool (in my example, 2 events) only as many times as there are rare events to be found. This means of course that the process of collecting information on who executed the trials (purchased the boosters) and running the raffle itself should be carefully prepared to avoid mistakes and maintain trust in the process. Still, from a coding perspective, I don't see why that would be more difficult than implementing an algorithm such as the one I showcase here.
A more elaborate raffle solution would be to distribute a moderately higher number of tickets during the trials (booster opening) and then run a raffle on those tickets. This has the disadvantage of creating a slightly more convoluted process, but it's not that uncommon. The upsides would be:
immediate excitement upon seeing the outcome of the trial and finding a ticket (opening a booster), potentially prompting opening more;
social buzz around the tickets generates interest and could convince more people to participate;
trading and speculation among ticket holders before the raffle is conducted. Ticket trades generate a benefit from the raffle for more people who otherwise wouldn't gain anything extra.
All in all, I think a raffle system is a more straightforward and fair solution. It can still be automated to reduce the risk of human error. For trust and transparency it would also require being presented in a format where the data and the process can be verified, which may add a bit of overhead, but I think if implemented correctly it creates a fairer system in the end.

The rewards earned on this comment will go directly to the people( @agrante ) sharing the post on Reddit as long as they are registered with @poshtoken. Sign up at https://hiveposh.com. Otherwise, rewards go to the author of the blog post.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.
Congratulations @agrante! You have completed the following achievement on the Hive blockchain And have been rewarded with New badge(s)
Your next payout target is 2000 HP.
The unit is Hive Power equivalent because post and comment rewards can be split into HP and HBD
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPCheck out our last posts: