Introduction
When it comes to tips and strategies for improving your success playing Gods Unchained, two of the mandatory topics will always be deckbuilding and the mulligan phase. Since we can have 1 or 2 copies of the same card (bar Legendaries) in most game modes, there is a lot to be said about those decisions. But when a particular card is critical to have in hand early on, the best probabilities always come from having 2 copies of every possible card. And that has a lot to do with how the game selects the initial 4 cards, which in turn is heavily affected by your choices during the mulligan phase.
Explaining the reason for this is the topic of this post, including a little program to help make the calculations involved in those choices. I will start by discussing the odds for 3 different scenarios and leave the discussion of the code that produced those results to the end.
Game start and mulligan phase
At the start, the game presents you with 3 random cards from your deck. If your deck has duplicates, it is possible to have both copies presented to you in this initial group of 3 cards.
You then have the option to replace (mulligan) cards that you are not interested in having in your hand when the match starts, perhaps because the mana cost is too high, or you're fishing for specific cards critical for the deck's strategy, for example.
In Gods Unchained you are offered 3 opportunities to replace cards during the mulligan phase if you are going first; you get 4 opportunities if you are going second.
An important and not so obvious rule is that when you mulligan a card away, the game will not present you with that card again OR a second copy of that card, if one exists in your deck; since you are not interested in the first copy, surely you won't be interested in the second copy as well. The consequence is that the chance of finding a card you are looking for actually increases slightly for each mulligan swap, because the cards you mulligan away won't be shown to you again.
To put it another way - the pool of possible cards the game can choose to show you is reduced as the mulligan phase progresses and thus the chance of finding the card you want increases (there are fewer cards to choose from). Additionally, if the card you mulligan away has a copy, the chances of finding a card you need increase even more, because then there are 2 cards that cannot be chosen again during the mulligan phase, instead of just 1.
Once you spend all your mulligan changes or accept the current hand, the game 'forgets' the mulligan restrictions and picks a fourth card from your remaining deck, completing your starting hand with 4 cards in total.
Simulation results
I ran 6 simulations:
Coronet Combo Magic deck with 14 pairs and 2 singles (Divine Coronet and Giramonte) - going first and going second;
Any deck with 15 pairs (zero singles) - going first and going second;
Any deck with just singles (30 different cards) - going first and going second;
Since the outcome is binary 'card was found at the start of the game' / 'card was not found', the simulation needs to be repeated multiple times to calculate the average over a large number of matches (trials).
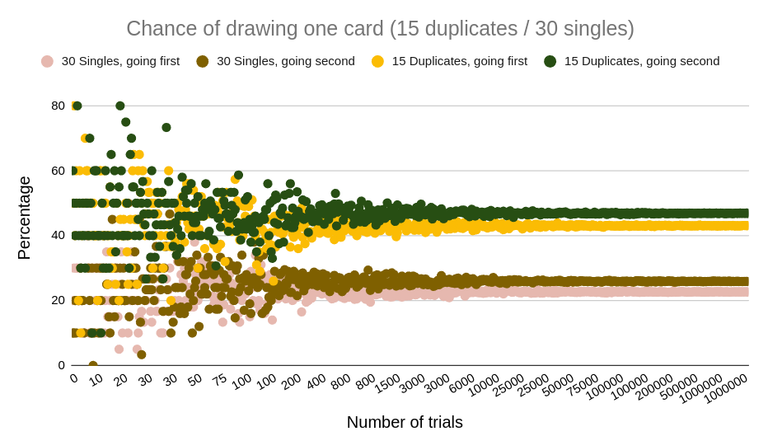
I calculated averages for a list (array) of the number of trials / simulations, starting from 10 all the way to 1 million simulations. The purpose of this was to visually identify in a graph when the probability starts to become stable as the number of simulations increases. This gives an idea of the minimum number of trials necessary to reach a point where further trials will not decrease the variance of the result (the result being the percentage).
On the other hand, the trials themselves can have variance, which is particularly noticeable in trials with a very low number of simulations (see table below). So the script also repeats each group of trials 30 times (iterations) to generate variance data at each set of simulations. Plotting the simulation results in this manner provides a simple method of stabilization of variability and allows for a visual determination of the minimum sample size (number of trials) necessary to guarantee a precise and accurate result.
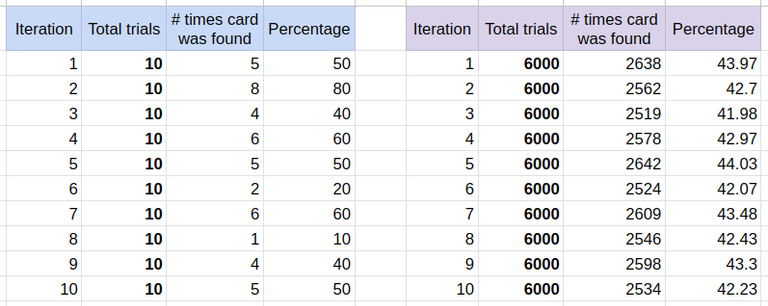
You can check the raw data and the graphs in this Google Spreadsheet.
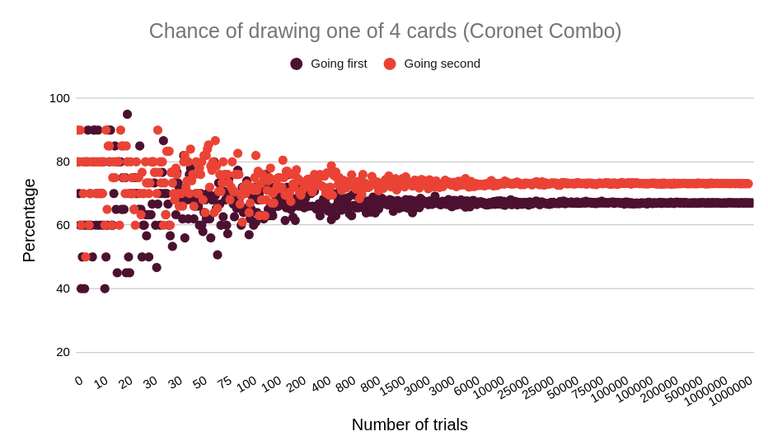
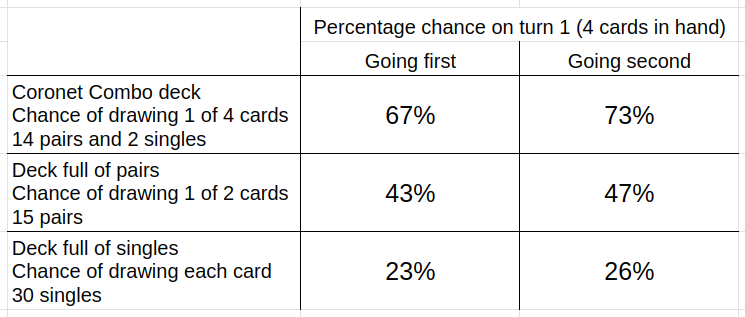
Example with a Coronet Combo Magic deck
Going first, the chance of getting 1 of 4 cards is approx. 67%.
Going second, the chance of getting 1 of 4 cards is approx. 73%.
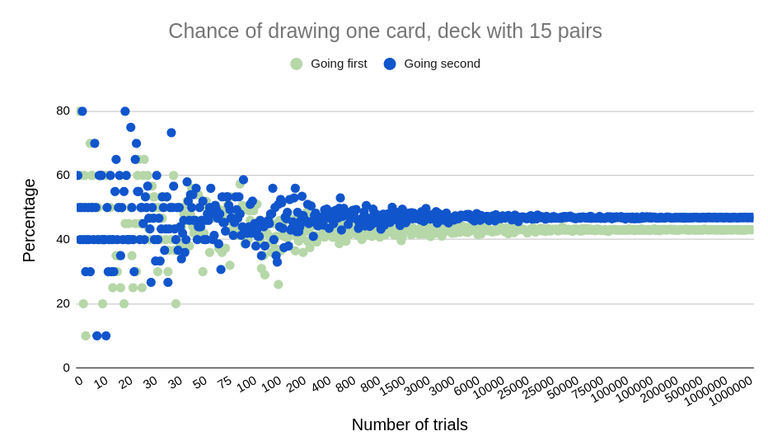
Example with a deck full of pairs
Going first, the chance of getting 1 of 2 cards is approx. 43%.
Going second, the chance of getting 1 of 2 cards is approx. 47%.
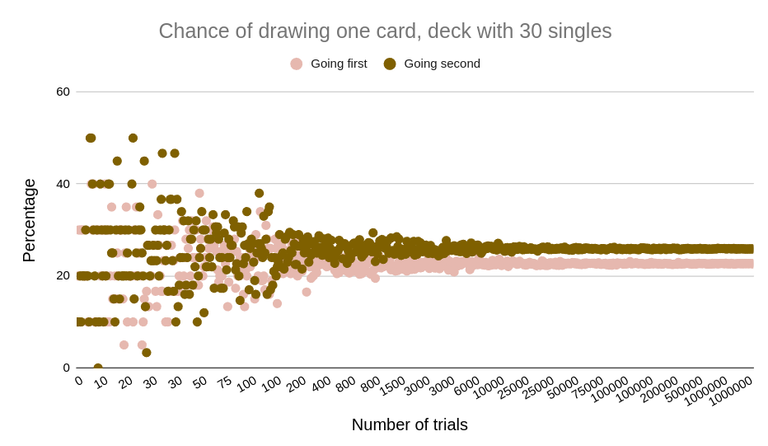
Example with a deck full of singles
Going first, the chance of getting 1 card is approx. 23%.
Going second, the chance of getting 1 card is approx. 26%.
Conclusion
From a visual inspection of the graphs, the minimum number of simulations required for a really tight, accurate and precise result, is between 3-10k. I would say the variance starts to stabilize to acceptable levels around 1k trials.
Coronet Combo Magic has a crazy probability of at least 2 in 3 games of having Lost in the Depths, a critical card to be played early in the game, on turn 1. This, paired with the high number of Forsee cards in the rest of the deck, makes reaching the deck's win condition on time extremely consistent.
In a deck full of pairs, the chance of getting any one important card at the start of the game is a little under 50%. In a deck like Olympian War, where it would be very desirable to have 2 cards in hand at the start of the game (Village Vendor and Parthene Guardian), the best odds of that happening would be approximately 0.47 * 0.47 * 100 = 22%, when going second. Of course, a strong start doesn't need both cards on turn one, but this is just an example. The code can be easily modified to simulate the hand state in subsequent turns by wrapping the assignment of
firstDrawin line 88 in a loop.In a deck full of singles, the chance of getting any one important card at the start of the game is around 25%. Comparing these results with the results from a deck full of pairs explains why duplicates are important for consistency, especially when certain cards in the deck are very desirable to be drawn early in the game.
Here is the tldr; main point of this article:
Javascript code to simulate the start of the game and calculate the odds
This script was executed with Node.js on Ubuntu. I'm not sure which changes would be necessary to run it in Windows. Maybe the path to the .csv file would need to be indicated differently.
Below is the code I used to generate the results. A few adjustments can be made to change the initial conditions. The results I got seem pretty plausible, but there is always the possibility of mistakes. If you find a bug, please let me know in the comments. I left a lot of commented out console commands that are helpful for troubleshooting and making modifications. Next I will explain which parts of the code can be modified to test different conditions.
The first array represents a typical Magic Coronet Combo deck, with 14 pairs and 2 singles (Divine Coronet and Giramonte). When testing this deck setup you're always looking for 1 of 4 cards, so the variable
targetIDsshould point to any 2 duplicated numbers indeckArray.The second array represents a deck with 15 pairs of cards (zero singles). Typically one would be interested in calculating the odds of finding 1 of 2 copies of the same card, so the variable
targetIDscan point to any number indeckArray.The third array represents a deck with 30 different cards (zero pairs). Typically one would be interested in calculating the odds of finding a single card, so the variable
targetIDscan point to any number indeckArray.You can modify the array to represent your particular deck and calculate the odds for any specific situation you may be interested in.
When choosing decks and making modifications, make sure that only one of the 3
deckArrayvariables is active and the others are commented out.The code will calculate the average probability of drawing the desired card(s) from a total of trials indicated in
totalTrials. Each average is calculated 30 times (k) to create a visual representation of the variability of the averages.With the purpose of just calculating final results (without all the parameter testing), you can set
totalTrials = [10000]in line 19 andk < 1in line 119. You will the able to read the percentage value in the console (the .csv file is not necessary).As I mentioned earlier, the code can be easily modified to simulate the hand state in subsequent turns by wrapping the assignment of
firstDrawin line 88 in a loop.
const fs = require('fs');
// Coronet Combo
const deckArray = [1, 1, 2, 2, 3, 3, 4, 4, 5, 5, 6, 6, 7, 7, 8, 8, 9, 9, 10, 10,
11, 12, 12, 13, 13, 14, 14, 15, 15, 16];
// Full duplicates
//const deckArray = [1, 1, 2, 2, 3, 3, 4, 4, 5, 5, 6, 6, 7, 7, 8, 8, 9, 9, 10, 10,
// 11, 11, 12, 12, 13, 13, 14, 14, 15, 15];
// Full singles
//const deckArray = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15,
// 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30];
var decklist;
var hand = [];
const targetIDs = [1, 2]; // [1] if looking for 1 card §##§ [1, 2] if looking for 2 cards
const mulliganSwaps = 3; // Going first: 3 §##§ Going second: 4
let totalTrials = [10, 20, 30, 50, 75, 100, 200, 400, 800, 1500, 3000, 6000, 10000,
25000, 50000, 75000, 100000, 200000, 500000, 1000000];
//let totalTrials = [1];
const SimpleDraw = () => {
const randomIndex = Math.floor(Math.random() * decklist.length);
const drawnCard = decklist[randomIndex];
// Remove the card from the deck
decklist.splice(randomIndex, 1);
// And add the card to the hand
hand.push(drawnCard);
return drawnCard;
}
const MulliganSwap = () => {
const randomIndex = Math.floor(Math.random() * decklist.length);
const drawnCard = decklist[randomIndex];
// Remove all occurrences of the drawn card
decklist = decklist.filter(card => card !== drawnCard);
// Update the hand
hand[0] = drawnCard;
return drawnCard;
}
const CheckPick = (cardID) => {
if (targetIDs.includes(cardID)) {
//console.log(`\x1b[32mTarget card found: ${cardID}\x1b[0m`);
return true;
}
}
const DrawOneGame = (arr) => {
decklist = [...arr]; // Create a shallow copy
//console.log("\x1b[1mNew game start\x1b[0m");
//console.log(`Original deck: ${deckArray}`);
//console.log(`Starting deck: ${decklist}`);
for (let i = 0; i < 3; i++) {
const pickedCard = SimpleDraw();
//console.log(`Mulligan Card #${i+1}: ${pickedCard}`);
//console.log(`Remaining deck: ${decklist}`);
if (CheckPick(pickedCard)) {
return true;
}
}
for (let j = 0; j < mulliganSwaps; j++) {
const pickedCard2 = MulliganSwap();
//console.log(`Mulligan Swap #${j+1}: ${pickedCard2}`);
//console.log(`Remaining deck: ${decklist}`);
if (CheckPick(pickedCard2)) {
return true;
}
}
// Before drawing the 4th card, reset the card list without the restrictions of the mulligan
//console.log(`Decklist before mulligan: ${decklist}`);
//console.log(`Hand after mulligan: ${hand}`);
decklist = arr.filter(card => card !== hand);
//console.log(`Decklist after mulligan: ${decklist}`);
const firstDraw = SimpleDraw();
// Reset hand array for next iteration
hand = [];
//console.log(`First Draw: ${firstDraw}`);
//console.log(`Remaining deck: ${decklist}`);
if (CheckPick(firstDraw)) {
return true;
}
//console.log("\x1b[31mTarget card not found\x1b[0m");
return false;
}
// START HERE
console.log(`Original array ${deckArray}`);
console.log("Array size:", deckArray.length);
// Clear the .csv results file and write the header
var dataCSV = "";
const pathCSV = './mulligan_results.csv';
const eventLabels = "Iteration,Total_Trials,Card_Found,Percentage\n";
fs.writeFile(pathCSV, eventLabels, (error) => {
if (error) throw error;
});
// Main loop
totalTrials.forEach(value => {
for (let k = 0; k < 30; k++) { // k < 30
let foundCard = 0;
for (let l = 0; l < value; l++) {
if (DrawOneGame(deckArray)) {
foundCard++;
}
}
const percent = (foundCard / value * 100).toFixed(2);
dataCSV += `${k+1},${value},${foundCard},${percent}\n`;
console.log("Target card found:", foundCard, "times");
console.log("Total Trials:", value);
console.log("Chance of finding target card(s):", percent, "%");
}
})
console.log(`Original array ${deckArray}`);
console.log("Array size:", deckArray.length);
// Save data to file
fs.appendFile(pathCSV, dataCSV, (error) => {
if (error) throw error;
});
Click here for color-coded Gist.
If you make the loop shorter, with fewer totalTrials / k < 1 (to avoid a 'stdout maxBuffer length exceeded' error), you can execute the script online at https://onecompiler.com/nodejs/43699zb26
This post was published with PeakD: a community website built on the Hive blockchain. It is a blogging platform with some similarities to Reddit, except everyone gets paid to post, gets paid to comment and gets paid to vote. There is a long-established GU community here. If you're interested in joining, I can help you onboard and take the first steps with boosted rewards - drop me a message.

The rewards earned on this comment will go directly to the people( @agrante ) sharing the post on Reddit as long as they are registered with @poshtoken. Sign up at https://hiveposh.com. Otherwise, rewards go to the author of the blog post.
oo this is good!
Thanks! :P
You're welcome to use the code in GUmeta, if this gave any ideas lol
!PIZZA
$PIZZA slices delivered:
(6/10) @danzocal tipped @agrante