Realizaremos el análisis estructural de un arco parabólico simplemente apoyado, sometido a dos cargas externas. Ya en la anterior publicación, abordamos las ecuaciones generales necesarias para el cálculo de las solicitaciones en cualquier punto de un arco. Esto se realiza conociendo primero los parámetros geométricos para calcular luego los parámetros estructurales.
El ejercicio a realizar es el siguiente:
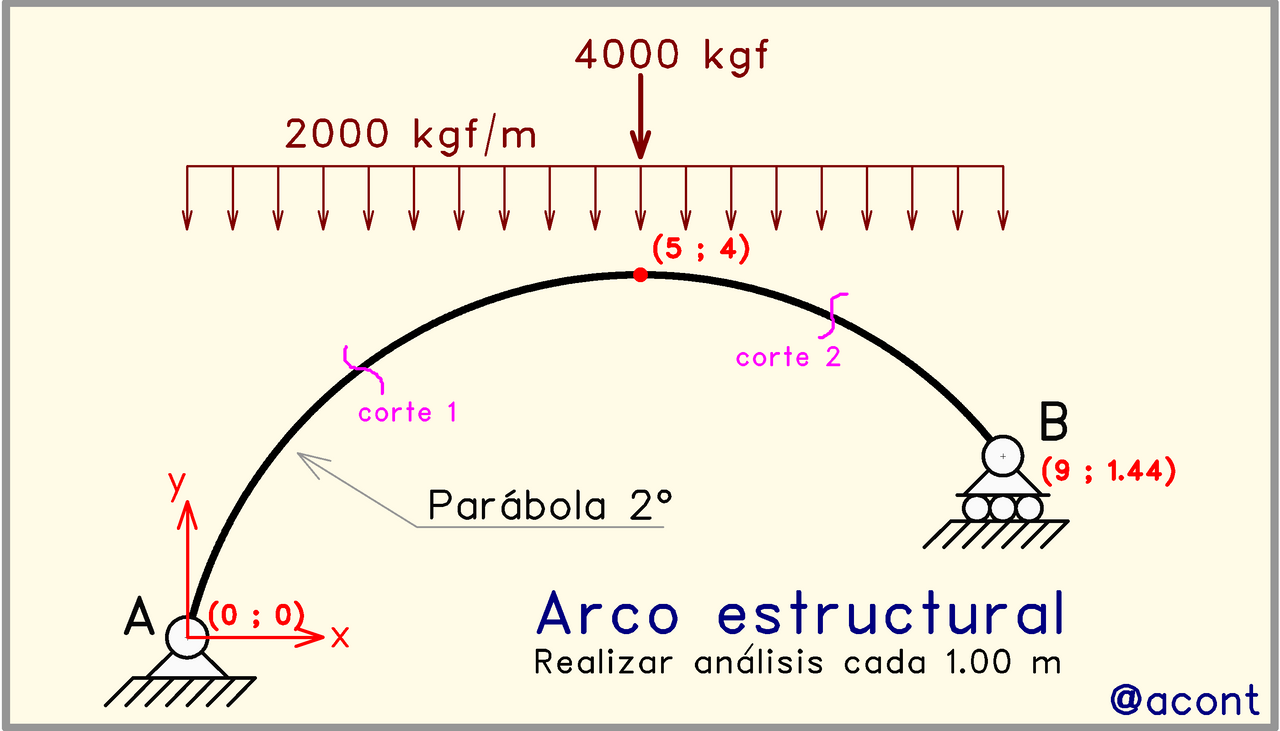
Se muestra un arco en el que cada punto de interés posee coordenadas que utilizaremos luego para realizar la parte geométrica. El arco parabólico está sometido a una carga distribuida uniforme de 2000 kgf/m en toda su longitud, mientras que existe una carga puntual de 4000 kgf dirigida verticalmente hacia abajo en el punto más alto.
Geometría
Previo a abordar el cálculo de los parámetros estructurales, definiremos la geometría del arco, encontrando la función matemática que la describe. La ecuación de una parábola de segundo grado posee tres parámetros desconocidos “a”, “b” y “c”, los cuales determinaremos a partir de las coordenadas dadas:
Las tres coordenadas nos sirven para determinar estas tres incógnitas, lo cual nos lleva a la función matemática deseada. Cabe destacar que el parámetro “c”, no siempre es nulo, puede tener un valor distinto de cero en casos de arcos que poseen varias funciones matemáticas que definen su forma.
Cálculo de reacciones externas
Debemos conocer primero las reacciones externas en los vínculos de apoyo, para ello, empleamos las ecuaciones de equilibrio estático:
Cálculo de reacciones internas
Ya definidas las reacciones externas, podemos pasar a realizar cortes en diversos puntos del arco para encontrar las fuerzas internas que actúan. Observando el arco, vemos que posee dos tramos o intervalos, ya que existe una discontinuidad en el sistema de cargas externo dado por la carga puntual de 4000 kgf. La carga distribuida se distribuye uniformemente en todo el arco, por lo que esta no introduce ninguna discontinuidad.
Por otro lado, si la carga distribuida se interrumpiera en algún punto intermedio del arco, dicho punto sería una discontinuidad, sumada a la discontinuidad que ya genera la carga puntual.
Tenemos, por lo tanto, dos tramos, y necesitaremos realizar dos cortes en la estructura, uno para cada tramo. Esto se realiza con la finalidad de hallar, para cada tramo, una ecuación genérica que describe a la fuerza horizontal, a la fuerza vertical y al momento flector.
Corte 1-1:
Producto del corte, obtenemos el siguiente subsistema:
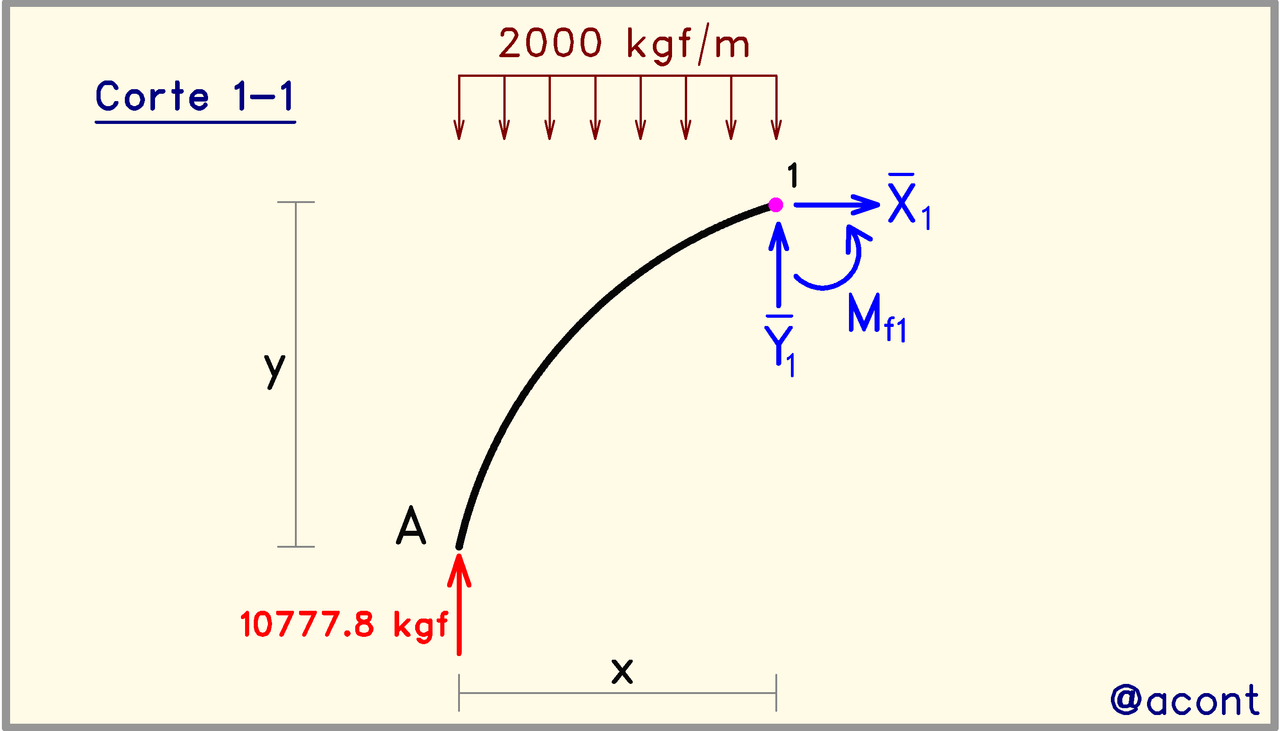
El punto de corte se encuentra alejado a una distancia “x” del origen del arco en horizontal, y a una distancia “y” en vertical. Esto nos permite hallar la ecuación de las fuerzas horizontal, vertical y de momento flector en un punto genérico del subsistema:
Corte 2-2:
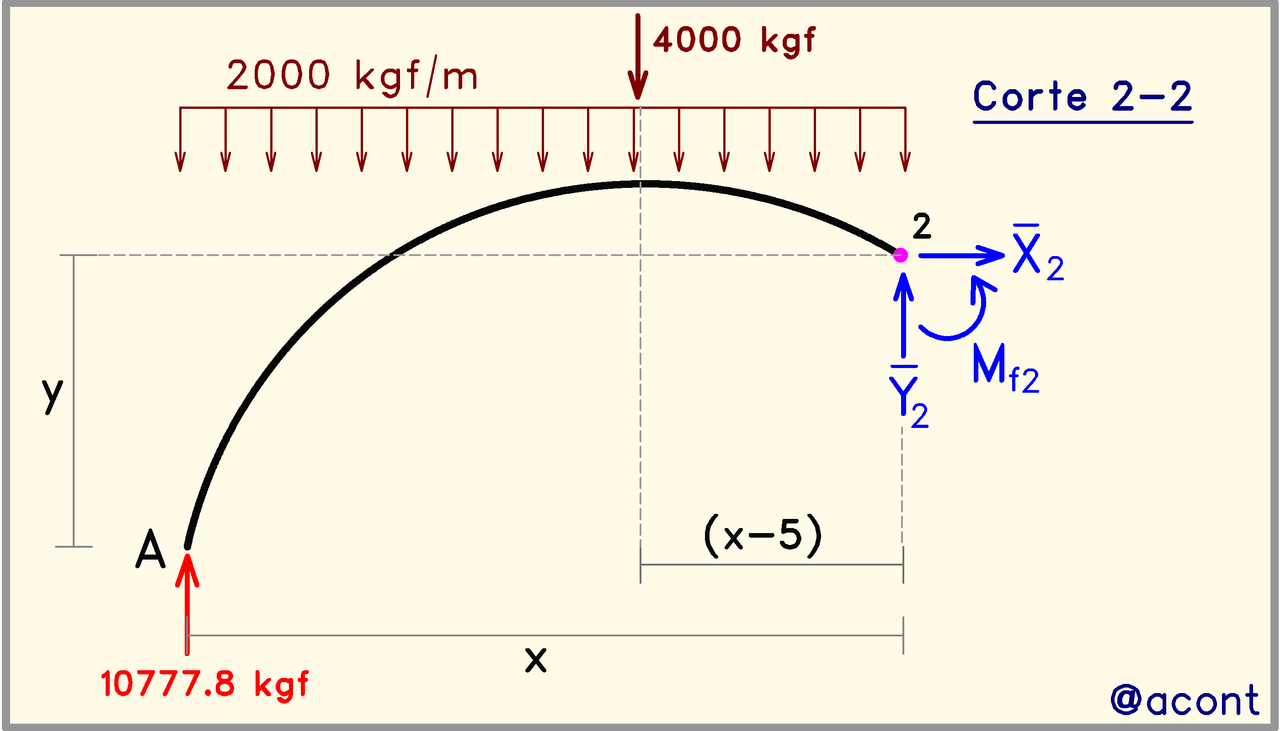
Realizamos lo mismo para el tramo restante, solo que esta vez nos aparecerá la fuerza puntual de 4000 kgf. Las distancias genéricas siguen siendo “x” y “y”, pero en las ecuaciones ahora aparecerá la fuerza puntual:
Una vez halladas las ecuaciones para las fuerzas internas en un sistema general (horizontal-vertical), debemos proyectar dichas fuerzas a un sistema de ejes locales (tangente-perpendicular al arco), para así hallar las fuerzas axial y cortante que actúan en cada punto del arco. El momento flector no requiere proyección, este ya puede ser calculado para cualquier punto del arco.
Ecuaciones de transformación geométrica
Ya en la anterior publicación se determinaron las ecuaciones generales para transformar las reacciones internas en solicitaciones orientadas según los ejes locales:
Solo nos queda definir la derivada de la función que define al arco: y’=f’(x).
Vamos a introducir todos los parámetros ya conocidos en las ecuaciones generales de transformación geométrica para cada tramo:
De esta manera, obtenemos ecuaciones que definen las solicitaciones en cualquier punto del arco con solo introducir el valor de “x” deseado. En el caso del momento flector, la ecuación ya fue definida anteriormente.
Cálculo de solicitaciones
Finalmente, podemos construir una tabla que muestre el valor de las solicitaciones en el arco cada @1.00 metros. En el caso de las solicitaciones cuya ecuación esté en función de la distancia “y” (lo cual no sucede en este caso), solo debemos sustituir “y” por la ecuación f(x) ya hallada previamente.
Mediante el uso de una hoja de cálculo, se puede simplificar en gran medida la realización de esta tabla, ya que solo debemos introducir una vez la ecuación de la solicitación para cada tramo. La siguiente tabla ilustra el resumen de cálculos de las solicitaciones al arco parabólico de este ejercicio:
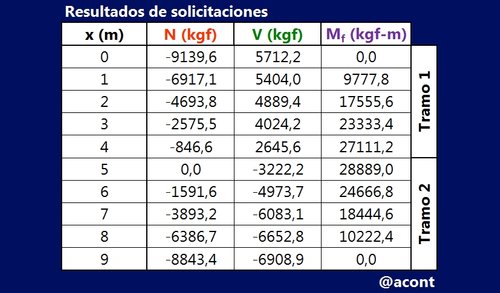
Para corroborar que estos resultados sean correctos, el valor final de la tabla debe coincidir con lo observado en la imagen de la estructura. La presencia de una articulación móvil (patín) al final del arco, indica que dicho punto no posee restricción rotativa, y por lo tanto el momento será nulo. Esto se comprueba al observar el resultado final en la tabla.
La configuración de las cargas indica que el arco debe estar sometido a compresión en toda su longitud, lo cual se refleja en la tabla, donde la fuerza axial arroja solo valores negativos. Además, se puede verificar que el valor obtenido en fuerza axial en los extremos del arco no supera en magnitud a los obtenidos en las reacciones de apoyo, ya que, en dicho punto, la fuerza axial es una componente de la reacción de apoyo, y debe poseer menor magnitud.
En el caso de existir rotulas o articulaciones internas, se debe reflejar en la tabla que el momento flector es nulo en los puntos donde estas se presentan, similar a lo que ocurre con los apoyos del presente ejercicio.
Aportes de esta publicación
| La presente publicación ilustra el proceso de cálculo de solicitaciones en miembros estructurales curvos. Se presenta la resolución de un ejercicio práctico en el cual se calculan las fuerzas axiales y cortantes y el momento flector en cualquier punto de un arco parabólico. Se presenta una aplicación práctica de las ecuaciones generales de transformación geométrica presentadas en la publicación precedente. |
Referencias
[1] Rodríguez, Iván. (2003). Estática de las Estructuras. (p. 124-133).Fuente
Material recomendado
•Análisis estructural de miembros curvos
Imágenes de autoría propia realizadas mediante LibreCAD y Microsoft PowerPoint. Tabla elaborada mediante Microsoft Excel.
Publicado mediante la dApp STEMsocial |
Visite la comunidad StemSocial y las etiquetas #STEMsocial y #STEM-espanol para encontrar contenido de calidad referente a Ciencias, Tecnología, Ingeniería, Matemáticas (STEM por sus siglas en inglés) y otros tópicos relacionados. STEMsocial es una comunidad con cuatro años de trayectoria conformada por autores de todo el mundo en la que se comparte y apoya la difusión de contenido STEM de calidad entre sus usuarios.
| Invitación al servidor de Discord de STEM-espanol: https://discord.gg/UJwQXWP | Registro en Hive |
¡Felicidades! Esta publicación obtuvo upvote y fue compartido por @la-colmena, un proyecto de Curación Manual para la comunidad hispana de Hive que cuenta con el respaldo de @curie.
Si te gusta el trabajo que hacemos, te invitamos a darle tu voto a este comentario y a votar como testigo por Curie.
Si quieres saber más sobre nuestro proyecto, acompáñanos en Discord: La Colmena.
Muchas gracias por el apoyo a esta publicación al equipo de @la-colmena 👍
Saludos amigo @acont. Muy útil este tipo de ejercicio para que estudiantes comprenden las aplicaciones prácticas del cálculo de este tipo de fuerzas y momentos que actúan sobre un arco parabólico, sobre todo por la importancia que tiene este tipo de estructuras en los métodos de construcción.
Efectivamente muy útil para los estudiantes, es bueno llevar este tipo de ejercicios a la web para que se difundan mejor. Saludos amigo @emiliomoron, gracias por comentar y tu visita.
Congratulations @acont! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s) :
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @hivebuzz:
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Thanks for using the STEMsocial app and including @stemsocial as a beneficiary, which give you stronger support.
Gracias por compartir tus conocimientos de tan alta calidad con todos nosotros y de tanta utilidad para los estudiantes y profesionales de dicha área, y de seguro para toda persona amante al conocimiento en general. Éxitos y bendiciones para tu familia.
Gracias por tu comentario valioso estimado @rbalzan79, éxitos y bendiciones igualmente para ti y sus seres queridos. Saludos.