Saludos, bienvenidos a este blog de Estática Aplicada, un área base de la Ingeniería Civil. Continuaremos con la Parte II de esta publicación dedicada al Momento Flector y sus diagramas.
La Parte I pueden encontrarla en el siguiente enlace: Estática Aplicada. Diagramas de Solicitaciones: Momento flector Parte I.
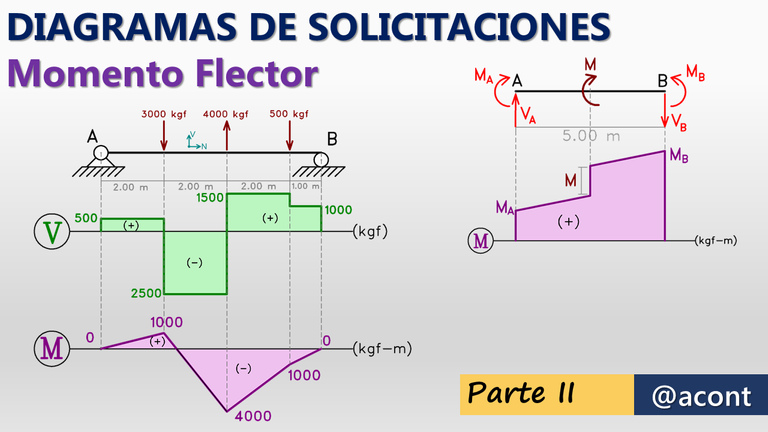
En esta serie de publicaciones ya abordamos los diagramas de fuerza axial, los diagramas de fuerza cortante y parte de los diagramas de momento flector:
•Diagramas de fuerza axial (N).
•Diagramas de fuerza cortante (V).
•Diagramas de momento flector (Mf).
•Aplicaciones prácticas de los Diagramas de Solicitaciones.
•Metodología para elaborar los diagramas de solicitación ante cualquier sistema de cargas.
Todo el material sobre Estática Aplicada se encuentra recopilado en la siguiente publicación:
Material de Estática Aplicada
Introducción |
Ya en la Parte I se estableció la diferencia entre momento y momento flector. El primer término, se refiere simplemente a un momento que forma parte de las cargas externas, representado como una “flecha que gira” (Fig. N°1).
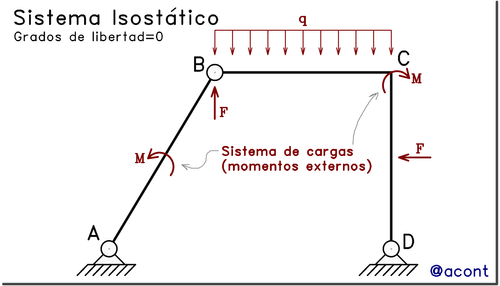
El momento flector, en cambio, es una carga interna (solicitación), que existe internamente, generada como respuesta ante la aplicación de cargas externas.
Es por ello que al realizar un corte en cualquier punto de un elemento sometido a cargas externas, se podrán reflejar allí las fuerzas que existen internamente, entre ellas el momento flector (Fig. N°2).
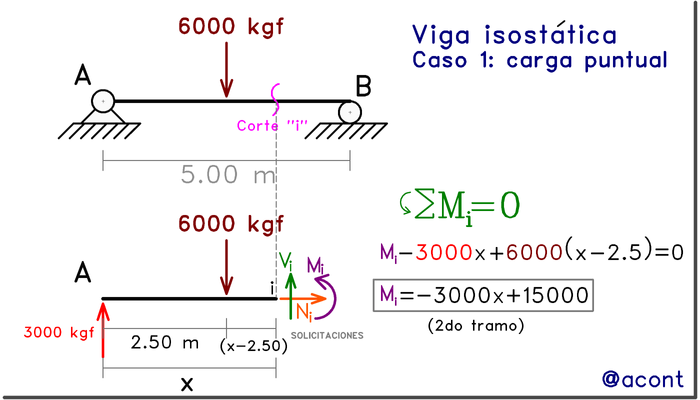
Dichas fuerzas existen para mantener el equilibrio interno del sistema.
Cada elemento lineal del sistema isostático posee un par de ejes locales “N” y “V”. Se suele asignar este sistema de coordenadas a las solicitaciones. Es por ello que tenemos fuerzas axiales y cortantes (N y V) y momentos flectores (M o Mf).
Ya observamos algunos aspectos importantes del momento flector en la Parte I de esta publicación. Ante cargas puntuales, el diagrama mostrará un comportamiento lineal con cambios de pendiente. Mientras que, ante cargas distribuidas uniformes, en diagrama presenta comportamiento parabólico. Esto se dedujo de la aplicación de ecuaciones de equilibrio estático en un punto de corte cualquiera.
En esta publicación, veremos desde un punto de vista más cualitativo, el efecto que tienen las cargas externas sobre dichos diagramas.
Efectos de cargas externas en la geometría de los diagramas de momento flector |
Las cargas externas que tienen incidencia sobre el momento flector son las que se dirigen en dirección del eje local “V”. Los momentos externos, por supuesto, tienen su incidencia en el diagrama de momentos flectores.
Las cargas axiales (“N”) no tienen efecto alguno, y son totalmente independientes, por lo que no nos interesan al momento de realizar el diagrama de momentos flectores. Es por ello que se suelen estudiar las solicitaciones en el siguiente orden: axiales, cortantes y momento flector (N, V y M).
Ausencia de cargas externas
Ya observamos en la Parte I de esta publicación que en los tramos o sectores donde no existe carga distribuida, el diagrama de momento flector presenta un comportamiento lineal con pendiente.
Se realizó la demostración mediante un corte en una barra sometida a una carga puntual. Se encontró una ecuación que expresa una relación lineal entre la magnitud del momento flector y la distancia “x” medida a partir del inicio de la barra.
Esta pendiente depende de la orientación y magnitud de las fuerzas puntuales cortantes presentes. Tomemos el ejemplo de la publicación anterior:
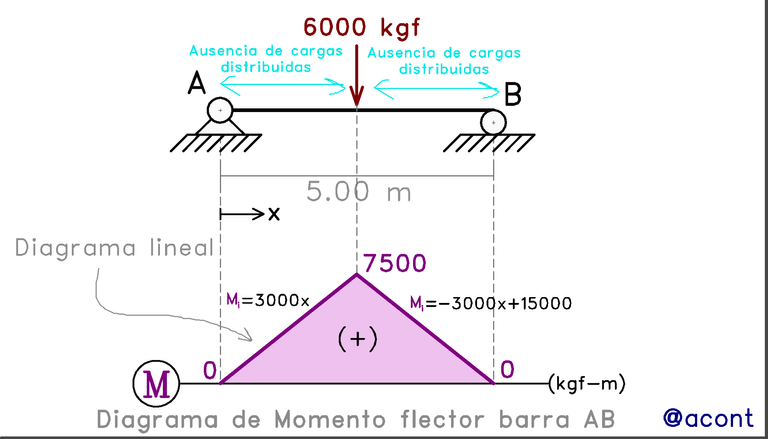
Podemos observar que un corte a ambos lados de la fuerza puntual, genera ecuaciones para el momento flector con pendientes de igual magnitud, pero signo distinto. En dicha publicación puede encontrar la demostración para dichas ecuaciones en el diagrama.
Podemos agregar que la magnitud de la pendiente depende de la magnitud de la fuerza cortante presente, tal como veremos más adelante. Podríamos imaginar que si la fuerza puntual de 6000 kgf presenta variación en su magnitud, se genera también variación en las reacciones de apoyo, modificando así la pendiente del diagrama.
Debemos tener presente que: el diagrama de momento flector nunca será constante (línea horizontal), al menos que la fuerza de corte sea nula.
Efecto de las fuerzas puntuales
Si observamos la figura N°3, podemos notar que la fuerza puntual generó un cambio de pendiente en el diagrama de momentos flectores.
Pero la pregunta es ¿Cómo se sabe el efecto que tendrá la carga puntual en el diagrama? La pendiente bien podría volverse más pronunciada, menos pronunciada, o incluso cambiar de signo (creciente a decreciente o viceversa).
En pocas palabras, las fuerzas puntuales que se dirigen hacia arriba tenderán a hacer crecer positivamente la pendiente, mientras que las que se dirigen hacia abajo tenderán a hacer que la pendiente sea más negativa. Sin embargo, esto se observaría con mayor claridad si visualizamos a la vez el diagrama de fuerzas cortantes.
Tomaremos el ejemplo abordado en la Parte I del Diagrama de Fuerzas Cortantes (Fig. N°4).
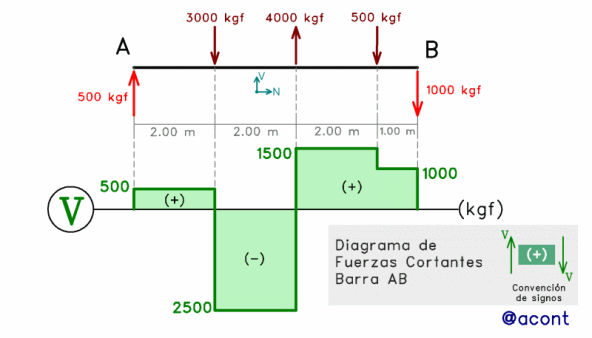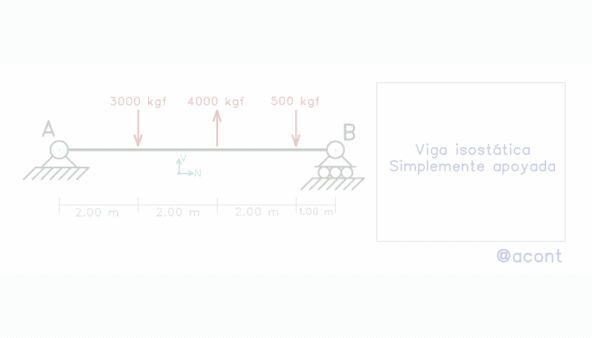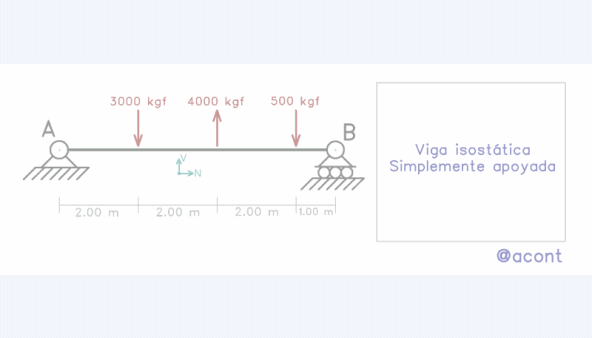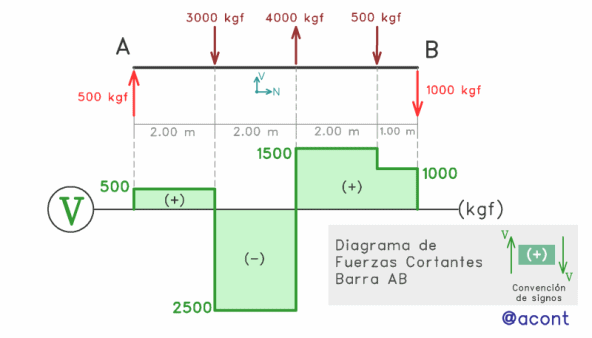
La fuerza cortante y el momento flector, son solicitaciones que están altamente relacionadas entre sí.
Sin tomar en cuenta el efecto de las cargas distribuidas, podemos decir que: cuando la fuerza de corte es positiva, la pendiente del diagrama de momento flector es positiva. Si la fuerza de corte es negativa, la pendiente es negativa.
Un aspecto práctico de importancia es que el área acumulada en el diagrama de corte, representa la magnitud del momento flector. Esto lo abordaremos en mayor profundidad en la Parte III, donde podremos ver la relación diferencial-integral entre ambas solicitaciones.
En la siguiente imagen animada, podemos apreciar cómo se traza el diagrama de momento en dicho caso.
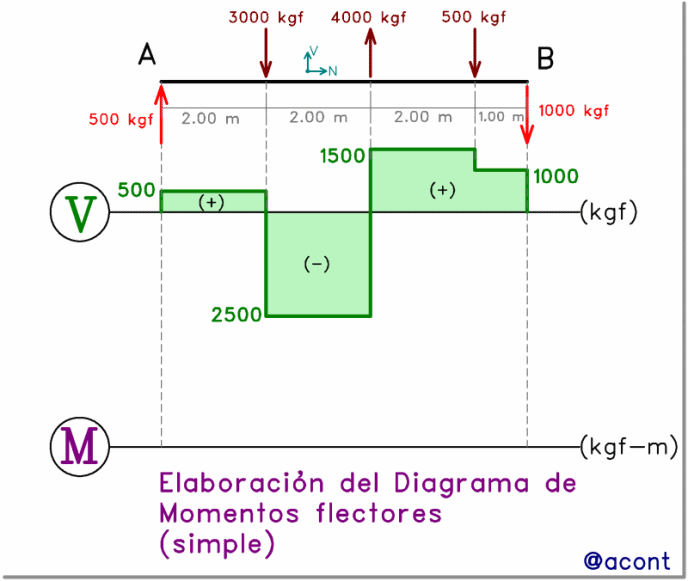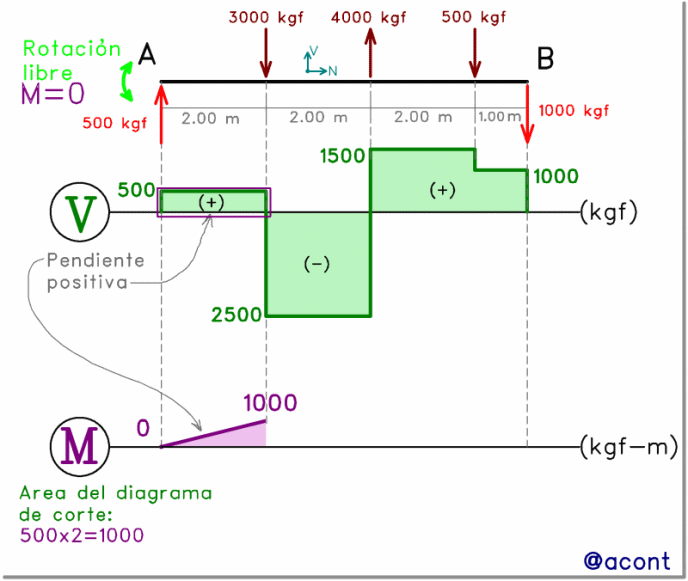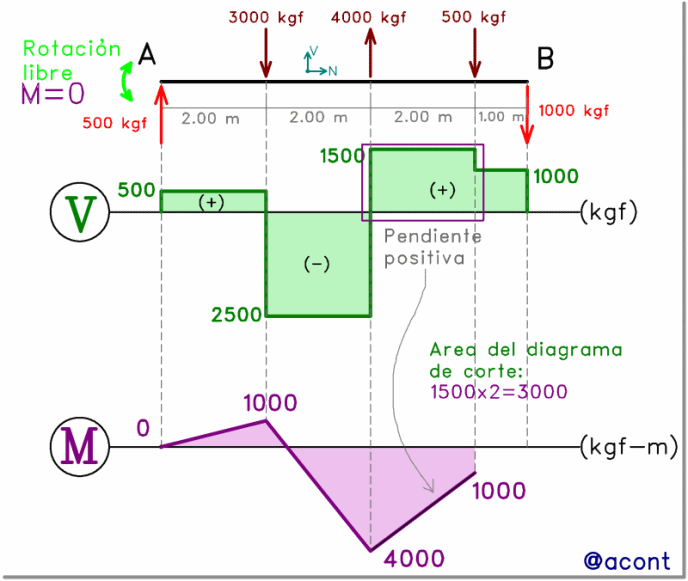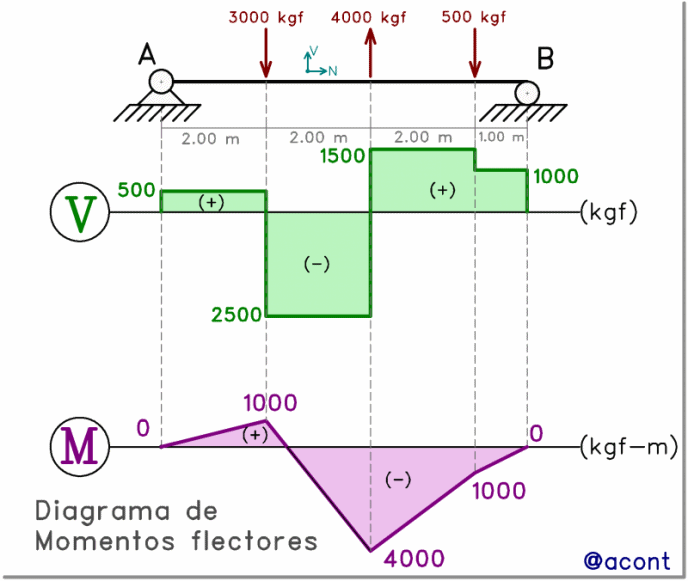
Cabe destacar que los vínculos de apoyo en “A” y “B” (Fig. N°4), presentan libre rotación, por lo que el momento flector será nulo en dichos puntos, tal como se refleja en el diagrama.
Se puede apreciar que las fuerzas puntuales de 3000 y 4000 kgf cambian el signo de la pendiente. Por otro lado, la fuerza de 500 kgf, al ser de pequeña magnitud y dirigirse hacia abajo, solo reduce un poco la pendiente del diagrama.
Efecto de los momentos externos
El efecto de los momentos en el diagrama es simple, generan un salto vertical.
Dicho salto será hacia arriba para momentos horarios y hacia abajo para momentos antihorarios, tal como se observa en la siguiente figura:
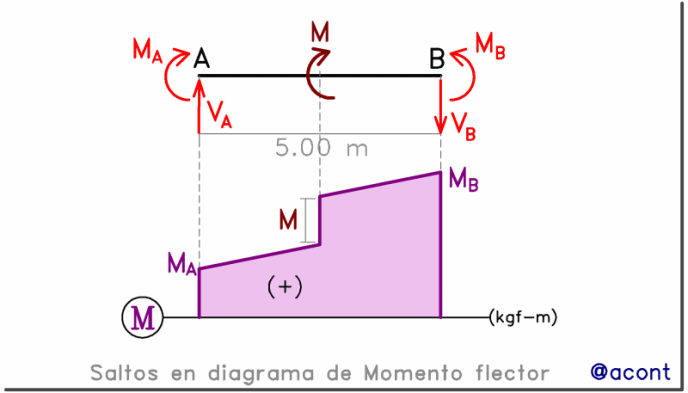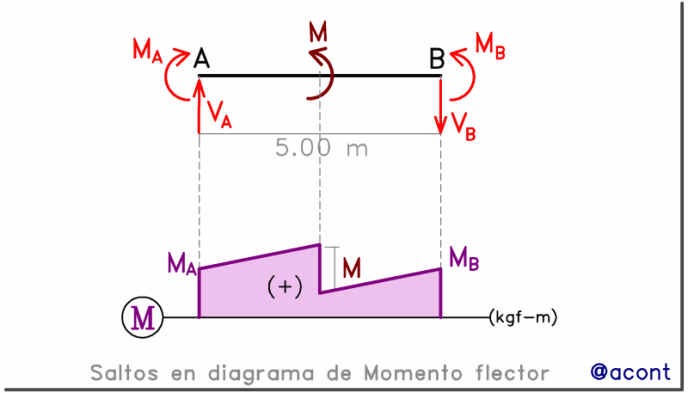
Esto sucede así porque se debe conservar el equilibrio estático en la barra (sumatoria nula de momentos).
Si el momento en el extremo izquierdo se orienta en sentido horario, y también lo hace el momento externo, entonces el momento en el extremo derecho debe ser lo suficientemente grande para contrarrestar a ambos (y también al momento producido por la fuerza de corte en “A”) y mantener el equilibrio.
Efecto de las cargas distribuidas uniformes
La presencia de cargas distribuidas uniformes o rectangulares, genera una forma parabólica en el diagrama. Esto se comprobó en la Parte I de esta publicación, la cual pueden consultar en el enlace al final de esta publicación.
Básicamente, la parábola tendrá concavidad negativa (abre hacia abajo) si la carga distribuida uniforme se dirige hacia abajo, tal como suele suceder en la mayoría de los casos. Veamos el caso abordado en la Parte I (Fig. N°7).
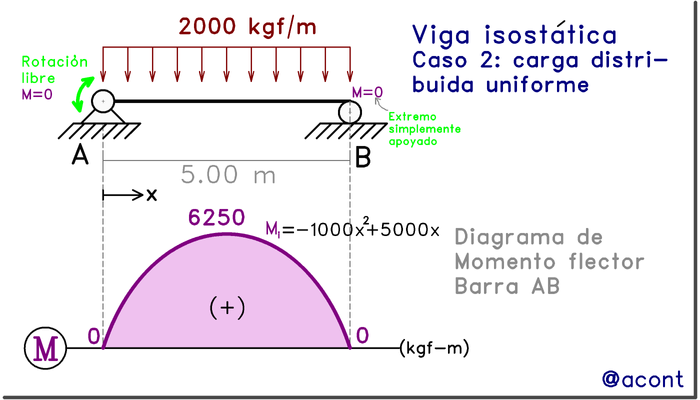
Si se reduce la magnitud de la carga distribuida, la parábola simplemente disminuye su valor máximo. Ya que dicho ejemplo es una viga simplemente apoyada, el momento flector será nulo en sus extremos.
Para el caso de carga orientada hacia abajo, si se presentase restricción rotativa en los vínculos de apoyo, el diagrama simplemente se trasladaría verticalmente hacia abajo, dando paso a momentos no nulos en uno o ambos extremos de la viga.
Nota: la convención de signos suele invertirse en cursos más avanzados en el área de estructuras para así adaptarse a las deformaciones. Si eres estudiante de estática, no te acostumbres a ver siempre la “parábola positiva” arriba del eje.
Efecto de las cargas distribuidas trapezoidales o triangulares
La presencia de cargas distribuidas con variación lineal o trapezoidales, generan una forma de función cúbica en el diagrama de momentos flectores. Suele necesitarse de una regla de signos o especie de “convención” para visualizar la concavidad del diagrama. Esto último lo profundizaremos en otra publicación.
Supongamos que tenemos una viga simplemente apoyada, sometida a una carga distribuida trapezoidal como en la siguiente Figura.
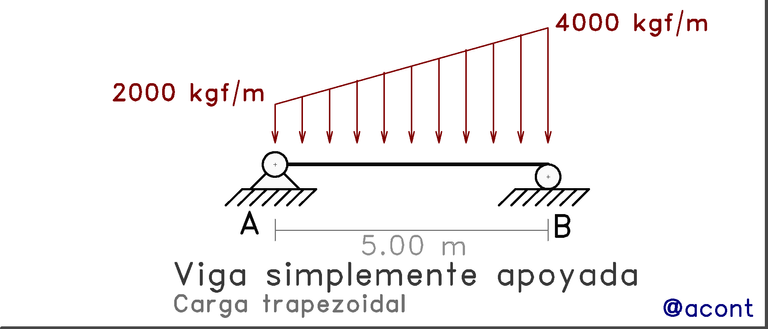
A diferencia del caso con la carga distribuida uniforme, el diagrama de momentos no será parabólico sino cúbico.
Este caso de carga no es tan común en la vida real como la carga uniforme o rectangular, sin embargo, a nivel académico se suele abordar con frecuencia. Es una forma de poner en práctica la habilidad para graficar el diagrama de momentos flectores, ya que es menos evidente que la forma parabólica.
El diagrama para el caso mostrado en la Fig. N°8 sería de la siguiente manera:
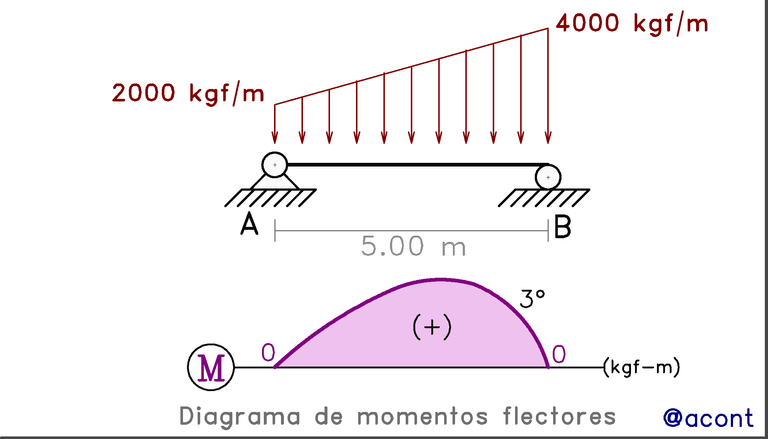
El cómo conseguir la ecuación que caracteriza al diagrama, será explicado con detalle en la siguiente publicación (Parte III). En dicha publicación, se dará explicación de las relaciones diferenciales e integrales entre las cargas externas, la fuerza de corte y el momento flector.
De esta manera, se dio una explicación de manera cualitativa del efecto de las cargas externas sobre la forma del diagrama de momentos flectores. Corresponde ahora ahondar en los aspectos cuantitativos para así obtener una caracterización más exacta del diagrama.
Aportes de esta publicación
| Los diagramas de momento flector presentan una forma geométrica dependiente de las características de las cargas externas. Se ha caracterizado el diagrama de momentos flectores según las cargas presentes y a partir de la información que nos proporciona el diagrama de corte. De esta manera, se aporta material desde el punto de vista académico en el ámbito de la Estática a la plataforma Hive. Se expresó cualitativamente, el efecto de distintas configuraciones de carga, para así adquirir una noción general del trazado del diagrama. Esta publicación aborda una manera simple de trazar el diagrama de momentos flectores, donde se contabiliza el área acumulada en el diagrama de corte y se va sumando a momento flector existente. |
Referencias Bibliográficas
[1]Norris, C. H. y Wilbur, J. B. (1973). Análisis Elemental de Estructuras. Segunda Edición. Libros McGraw-Hill de México. (p. 97-100).Fuente
[2]Rodríguez, Iván. (2003). Estática de las Estructuras. (p. 112, 119-123).Fuente
Material recomendado
•Las Ecuaciones de Equilibrio Estático y algunas aplicaciones en la Ingeniería Civil
•Estática Aplicada. Diagramas de Solicitaciones: Fuerza Cortante Parte I
•Estática Aplicada. Diagramas de Solicitaciones: Fuerza Cortante Parte II
•Estática Aplicada. Diagramas de Solicitaciones: Momento flector Parte I
Imágenes de autoría propia realizadas mediante LibreCAD y Microsoft PowerPoint. Gifs creados mediante Photoscape.
Publicado mediante la dApp STEMsocial |
Visite la comunidad StemSocial y las etiquetas #STEMsocial y #STEM-espanol para encontrar contenido de calidad referente a Ciencias, Tecnología, Ingeniería, Matemáticas (STEM por sus siglas en inglés) y otros tópicos relacionados. STEMsocial es una comunidad con cuatro años de trayectoria conformada por autores de todo el mundo en la que se comparte y apoya la difusión de contenido STEM de calidad entre sus usuarios.
| Invitación al servidor de Discord de STEM-espanol: https://discord.gg/UJwQXWP | Registro en Hive |
Excelente trabajo amigo @acont, un documento impecable, se nota el esfuerzo y la dedicación, te felicito que pases un excelente fin de semana !
Gracias por la apreciación compañero @amestyj, siempre buscando llevar buen contenido STEM a la plataforma Hive. Buen fin de semana igualmente.
#POSH
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Thanks for using the STEMsocial app and including @stemsocial as a beneficiary, which give you stronger support.
Excelente material el que presentas @acont, las explicaciones gráficas utilizadas son muy explicitas y con un diseño impecable...Saludos
Gracias por visitar @madridbg, saludos.
Excelente el abordaje que realizas en cómo influyen las cargas externas en la geometría del diagrama de momento. Muy didáctico. Felicidades amigo @acont. Gracias por compartir con la comunidad publicaciones tan interantes y de buena calidad. Saludos!!!
Eso es algo que los libros no suelen abordar en mucha profundidad y que es de gran aporte para el estudiante de estática. Gracias por la visita compañero @eliaschess333,un saludo!!
Excelente amigo, me hiciste recordar la regla de la mano derecha para calcular momento cuando vi estática en el 4to semestre de ingeniería de petróleo. Saludos y gracias por compartir
Que bueno que recuerdes la convención para los momentos compañero @carlos84. Que curioso, también vemos Estática en el cuarto semestre. Gracias por acercarte, saludos!
Inclusive mi estimado amigo cuando vi estática nos encontrábamos entre los alumnos que cursábamos la materia estudiantes de ingeniería mecánica, civil y petróleo porque todos la veíamos en el 4to semestre, saludos amigo y muchas gracias por compartir contenido interesante en el área de la ingeniería.
En mi caso, solo vimos Estática Aplicada los de Civil. Las otras carreras suelen ver Estática dentro de la materia Mecánica. Depende de cada universidad y us pensum.