Introducción a la Química Computacional: Superficies de Energía potencial y Método de Hartree-Fock
Luego del desarrollo de la Mecánica Cuántica, se necesitó recurrir a métodos de aproximación con la finalidad de obtener información de diferentes sistemas físicos. Propiedades como las superficies de energía potencial, y la energía total del sistema han permitido discernir si alguna simulación está acorde con la realidad. Entre uno de los métodos más importantes, se encuentra el método de Hartree-Fock, el cual abrió paso al desarrollo de una gran cantidad de métodos posteriores, en un desarrollo que aun continua para la Química Computacional.
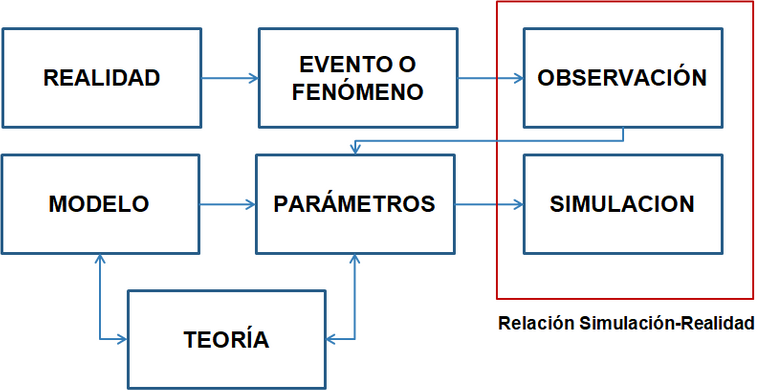
Desde la concepción del entorno por el hombre, el concepto de realidad siempre ha encabezado uno de los más grandes debates filosóficos. Según Kant, aquellos elementos que se encuentren en cierta dependencia con condiciones materiales de la experiencia. En este caso los métodos computacionales se basan en un modelo teórico (en algunos casos estrictamente teóricos, en otros incluyendo parámetros experimentales), para recrear de la mejor manera posible un entorno asociado a la realidad de algún fenómeno o evento físico de interés científico.
Es importante entender que cada uno de los cálculos que se utiliza, la química computacional amerita un modelo el cual debe estar fundamentado en alguna teoría. En este caso puede ser la teoría de la mecánica cuántica o de la mecánica clásica. Dicho modelo puede incluir o no parámetros empíricos y luego que se ha construido es posible llevar a cabo una simulación.
La simulación no es más que la recreación del contexto de un evento físico o un fenómeno físico. Esta recreación debe acercarse lo más posible a la realidad. En este caso se destaca principalmente la importancia que hay en la diferencia de la observación de algún fenómeno físico en la realidad con la observación de ese mismo fenómeno realizado mediante una simulación computacional, esta diferencia representa uno de los errores más notorios cuando se utilizan modelos computacionales, para estudiar eventos reales. Es importante también decir que dicha diferencia ha ido disminuyendo con el pasar de los años (desde la década de los 50), ya que se han venido creando programas que han implementado nuevos basamento teóricos, nuevos parámetros o nuevas técnicas matemáticas que han permitido disminuir este es terror haciendo que cada vez las simulaciones generadas sean mucho más cercanas a lo que se obtiene en la realidad.
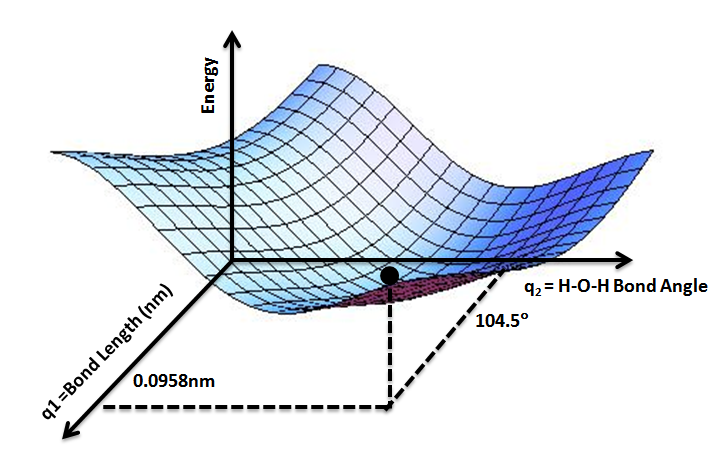
Una de las propiedades más útiles a determinar en química computacional, son las superficies de energía potencial (PES por sus siglas en ingles). La energía electrónica molecular puede ser descrita como una función dependiente de las coordenadas del núcleo de cada átomo que la constituye. Frecuentemente, estas funciones son multidimensional, y la variación de esta con respecto a sus coordenadas, se conoce como Hipersuperficie de Energía Potencial. El análisis de estas funciones se centra en la búsqueda de mínimos y máximos relativos y globales, así como el análisis de gradientes, derivadas direccional, y condiciones que involucren a las coordenadas correspondientes con un mínimo de energía.
En la figura anterior se observa cómo el valor de 104,5° representa un mínimo en energía para la molécula. Mediante análisis similar utilizando distintos métodos de derivación y/o minimización, es posible obtener la configuración espacial óptima dada una molécula problema.
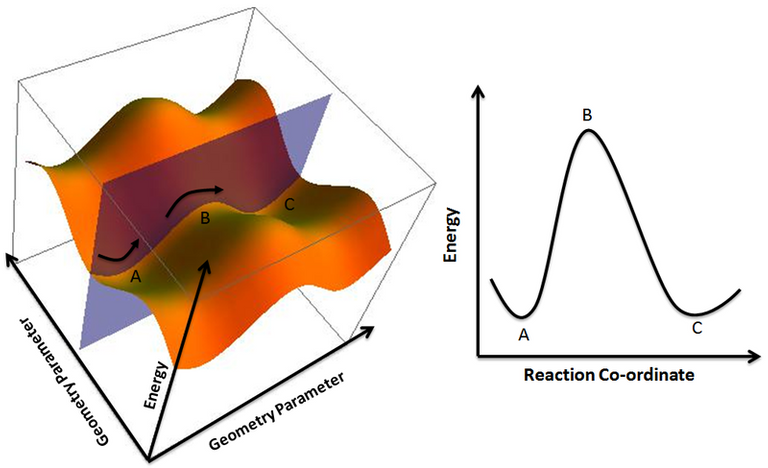
Sin embargo, el estudio de estas superficies no solo se limita a la obtención de geometrías óptimas, sino que permite además, el análisis energético relativo de productos y reactantes en una reacción química. Por lo general el punto más alto en energía para una reacción, el estado de transición, representa un punto de ensilladura en la superficie, es corresponde al camino de más baja energía entre los múltiples posibles caminos que puede conducir una misma reacción. Así pues, el estudio del estado de transición permite realizar análisis un poco más profundo, revelando información acerca de los cambios termodinámicos del sistema, y pudiéndolos relacionar con factores cinéticos a partir de la teoría del estado de transición. De esta forma se pueden hallar muchos más factores que posteriormente se comparan con los procesos o mediciones experimentales.
Los modelos utilizados para su obtención, son diversos, desde la Mecánica Cuántica, Mecánica Molecular, Dinámica Molécula hasta métodos que incluyen ciertos parámetros experimentales, los denominados métodos semiempíricos. Naturalmente, el contexto del problema a resolver influye en gran medida en la escogencia del método, a tal punto que, en ciertas ocasiones es necesario utilizar métodos híbridos, en los cuales se puede tratar un sistema a partir de diferentes enfoques.
Uno de los grandes desafíos de la química computacional, es obtener información de sistemas físicos para los cuales no existe hasta los momentos, un método matemático que permita resolver sus ecuaciones de forma exacta. Los métodos referentes a la Correlación Electrónica, intentan crear aproximaciones válidas para resolver el problema de múltiples cuerpos.
Las SEP son obtenidas mediante la implementación de teorías de optimización, por lo que la superficie calculada no es exacta, pero los métodos se tienen como objetivo minimizar los errores asociados.
En líneas generales, se debe plantear una función dependiente de diversas variables (centros atómicos, ángulos de enlace u otros grados de libertad de la molécula), luego implementar las restricciones de la función, las cuales son las que contextualizan el problema matemático de optimización en un entorno fisicoquímico.
Uno de los primeros métodos recurría al cálculo de la energía potencial en puntos cercanos a un punto i, luego escoger el punto mínimo y repetir el proceso anterior con la finalidad de ir modelando sucesivamente la SEP y encontrar un mínimo local. Con los avances que se han realizado, hoy en día se cuenta con métodos d optimización utilizando derivada primeras, segundas, derivadas direccional, análisis de gradientes entre otros.
Si bien es un proceso general, en gran parte de los casos, las moléculas son tan complejas, que manejar un gran número de variables representa un problema de computo, y por lo tanto se opta por calcular la SEP en el marco de las variables relevantes para un estudio (coordenada de reacción si se quiere estudiar una reacción en particular, o ángulos de enlaces si lo que se busca es optimizar la geometría), por lo que no siempre es posible calcular la SEP completa de una molécula.
Dado que, el potencial de un átomo polielectrónico se representa como un acoplamiento entre todas las interacciones coulómbicas de cada uno de los electrones. Algunos métodos intentan encontrar un campo de potencial promedio o efectivo, y mediante el uso del teorema variacional e iteraciones sucesivas se obtiene un campo autoconsistente para el sistema, con lo cual es posible resolver de forma aproximada las expresiones relacionadas con la energía y otras propiedades de interés.
Existen métodos perturbativos en los cuales se busca representar un problema completo en una sumatoria de términos de menor complejidad, en este caso la correlación electrónica presente en el Hamiltoniano de un átomo polielectrónicos o molécula, puede describirse como un término adicional. Otros métodos se fundamentan en principios estadísticos; aquellos métodos que contengan información netamente teórica son denominados métodos ab initio, tienen la característica de ser robustos, muy detallados, y requieren de un gran poder de cálculo, ofreciendo resultados de gran exactitud en problemas de no más de 100 átomos.
En busca de reducir el tiempo de cálculo, algunos métodos incluyen parámetros experimentales, dando lugar a los métodos semiempíricos, los cuales resultan bastante útiles en el estudio de sistema complejos, de muchos elementos, como pueden serlo las proteínas o supramoléculas orgánicas.
Entre uno de los primeros y más conocido de los métodos de aproximación se encuentra el método de Hartree-Fock. Una vez resuelto el problema asociado a la energía del átomo de hidrógeno utilizando los postulados de la Mecánica Cuántica, es necesario expresar el operador Hamiltoniano para todos los demás átomos de la tabla periódica. Esto no solo constituye uno de los problemas físicos más importantes, sino que abre paso a un gran abanico de posibilidades fundamentadas en aproximaciones. Douglas Hartree propuso un método aproximado para obtener la energía total en átomos polielectrónicos. Dicha propuesta luego fue corregida por Slater y Fock, obteniéndose uno de los métodos fundamentales de la Química computacional, el método de Hartree-Fock.
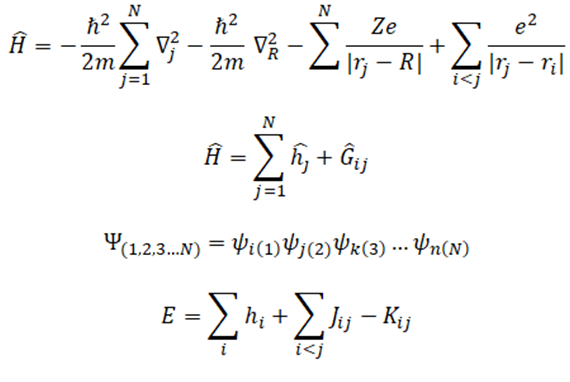
Teniendo con el operador Hamiltoniano de forma general, y las funciones de onda antisimétricas dadas por el determinante de Slater, se puede obtener la siguiente expresión para la energía mediante las reglas de Condon-Slater.
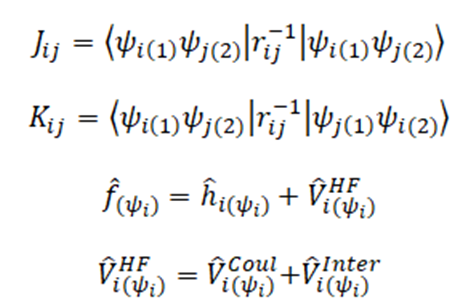
Esta aproximación se basa en la búsqueda de un potencial efectivo o promedio, que permita obtener la energía de cualquier función de onda sin tomar en cuenta directamente la correlación electrónica que existe entre todos los electrones presentes. Para ello, el operador de Fock se define a continuación. Dada las definiciones de la integral coulómbica y de intercambio, es posible encontrar una expresión general que contenga toda la información relacionada con el potencial del sistema, en este caso, se recurre al operador de intercambio para lograr obtener los términos correspondientes a la integral de coulomb.
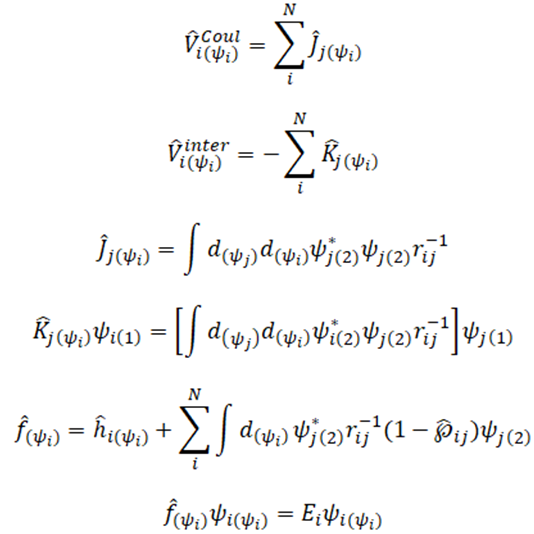
En síntesis, el operador de Fock permite encontrar la energía del sistema de la siguiente manera. En este caso no debe confundirse la expresión anterior con una ecuación lineal de autovalores y autovectores, ya que la dependencia que existe entre el operador y la función de onda utilizada no permite que este problema sea resuelto de forma lineal. Es en este punto donde el teorema variacional y el poder de computo hace posible que, mediante reiteradas iteraciones se consiga finalmente un campo promedio que además es autoconsistente con la función de onda de prueba expandida en una pase ortonormal del sistema. En general el esquema de trabajo a seguir es el siguiente:
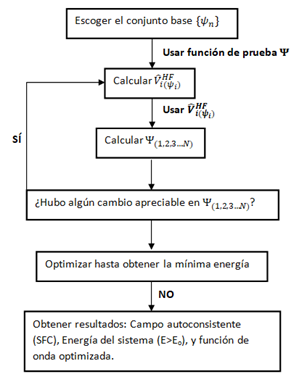
Es importante tener en cuenta que el potencial de HF se puede interpretar físicamente como un campo efectivo o promedio dentro del sistema de estudio. Dada la función de onda para un electrón, la evaluación del electrón i en el operador de Fock, contemplará la energía cinética y potencial del mismo, pero también un campo promedio que viene dado por todas le interacciones electrón-electrón del electrón i con los N-1 electrones restantes. De esta forma, y haciendo uso de la aproximación del método, se logran separar las variables de correlación electrónica, pudiéndose resolver el problema mediante el potencial promedio que se tiene en el sistema.
¿Por qué se dice que es un campo autoconsistente?
Se dice que es de Campo Autoconsistente porque el mismo proviene de un proceso iterativo que finaliza cuando la variación en la energía obtenida para el sistema es despreciable. Cabe mencionar que el potencial depende de las funciones de onda que se utilicen en el método. Inicialmente dicho potencial dependerá de las funciones de prueba que se escoja, pero a medida que el proceso iterativo mostrado anteriormente se ejecuta, las funciones de onda son optimizadas, pudiéndose calcular potenciales HF más exactos y con ello seguir el proceso de optimización de las funciones de onda. En el punto, en el cual este proceso converja a expresiones constantes para las funciones de onda (o para las energías del sistema), se dice que se ha obtenido un campo autoconsistente, con el cual, el cálculo de las funciones de onda a partir de mismo, son capaces de general nuevamente el mismo potencial para el sistema, sin alterar los valores de energía del mismo.

Es evidente que el desarrollo de la Química Computacional como rama de la Química General, va de la mano del desarrollo teórico, sin embargo se puede afirmar que dada las contribuciones de sus métodos, existe una retroalimentación en la cual la Química Computacional sirva de apoyo para el desarrollo teórico que se lleve a cabo en los próximos años.
Cada uno de los métodos planteados han sido mejorados hasta los métodos actuales, si bien es enorme la cantidad de éstos disponibles, se pudo observar cómo cada uno de ellos está construido sobre un enfoque especifico. Lamentablemente no existe un único método por defecto que resuelva todos los problemas en química y en bioquímica, en su lugar se disponen de nuevas alternativas, como lo es la inteligencia artificial, de los cuales se han obtenidos resultados alentadores. Es de esperarse que aquellos métodos post Hartree-Fock sean mejorados con la tecnología actual, haciendo posible un acercamiento mayor de la simulaciones con la realidad.
Gracias por leer.
Referencias:
Todas las imágenes y sepradores de mi autoría, fueron editados y procesados utilizando el programa PowerPoint 2016.
- [1] Andrew R Leach - Molecular modelling _ principles and applications-Prentice Hall (2001)
- [2] Warren J Hehre - A Guide to Molecular Mechanics and Quantum Chemical Calculations-Wavefunction (2003)
- [3] Andrew R Leach - Molecular modelling _ principles and applications-Prentice Hall (2001)
- [4] Frank Jensen - Introduction to Computational Chemistry-Wiley (2017)
- [5] Karol Jankowski (auth.), Stephen Wilson (eds.) - Methods in Computational Chemistry_ Volume 1 Electron Correlation in Atoms and Molecules-Springer US (1987)
Saludos @aleestra, muy buena introducción de este campo de la química, sobre todo para simular y dar respuesta a funciones tan complejas como las que se derivan de mecánica cuántica, especialmente lo que se refiere a al modelado de configuraciones electrónicas, para las cuales no hay modelos matemáticos simples que los puedan expicar.
Así es, no son para nada sencillas y es por eso que existen tantos métodos de aproximación. Lo bueno de todo esto, es que todos ellos se especializan en resolver problemas basgabte específicos y permiten obtener buenas aproximaciones para un sistema dado, sin duda un campo con gran futuro. Saludos y gracias por tu comentario @emiliomoron!
Muy importante aplicar los conocimientos del cálculo integral y las iteraciones para un tema tan importante como lo es las Superficies de Energía potencial. Gracias por compartir estos conocimientos con la comunidad de stem-espanol. Saludos
Si lo es, para los químicos es de gran importancia evaluar la reacciones químicas. En ese caso se evalúa la superficie de energía potencia entre los restantes y productos, con lo que se puede modelar el comportamiento de la reacción. Difinitivamente una excelente herramienta predictiva y a su vez teórica. Espero que lo haya disfrutado.
Muchas gracias por su comentario, un abrazo.
Bastante interesante como a través del cálculo y operadores se logre encontrar una solución aproximada a un problema complejo, encontrando así la solución más eficiente, en este caso en el ámbito químico. Gracias por compartir, saludos.
Si, en realidad este es uno de los primeros métodos, en la actualidad hay otros un poco más complicados que utilizan perturbaciones dependientes del tiempo entre otras herramientas. Pero como primera aproximación, el método de Hartree Fock ofrece una visión general de las capacidades que puede tener la mecánica cuántica a través de la química/física computaciónal.
Muchas gracias por tu comentario, un abrazo.
Su post ha sido valorado por @ramonycajal
Muchas gracias cervantes! 👍😊
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Thanks for including @stemsocial as a beneficiary, which gives you stronger support. Using the STEMsocial app could yield even more supporti next time.
Muchas gracias por su apoyo! 👍
#Twitter #posh
Congratulations @aleestra! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s) :
You can view your badges on your board And compare to others on the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @hivebuzz:
Support the HiveBuzz project. Vote for our proposal!