El objetivo de este post es ofrecer un tutorial para estudiantes de educación media y también a aquellos que van a iniciar estudios universitarios, sobre un tema de vital importancia para participantes de estos niveles educativos; tal tema trata la multiplicación de polinomios y los productos notables como un caso particular de dicha operación.

¿Qué método vamos a utilizar para introducir el tema?
Comencemos.
Como recordaremos, una expresión de la forma
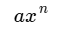
Recibe el nombre de monomio, sus elementos constitutivos son: la variable x, el coeficiente a (número que acompaña a la variable), y el exponente n el cual recibe el nombre de grado del monomio.
Nota
Se hace necesario recordar que cuando se suman dos monomios de diferente grado obtenemos un binomio, cuando sumamos tres monomios de diferente grado nos resulta un trinomio; y así, de manera sucesiva a partir de la suma de cuatro monomios en adelante obtendremos un polinomio cuyo grado será igual al grado del monomio sumando de mayor grado.
Consideremos los siguientes monomios y desarrollemos la multiplicación de los mismos:
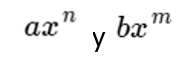
Esto es:
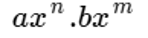
Para realizar esta operación, primero vamos a multiplicar coeficientes y luego sumaremos los exponentes (grados) de las variables semejantes, así:
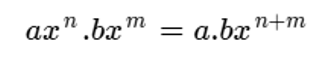
A continuación, algunos ejemplos:
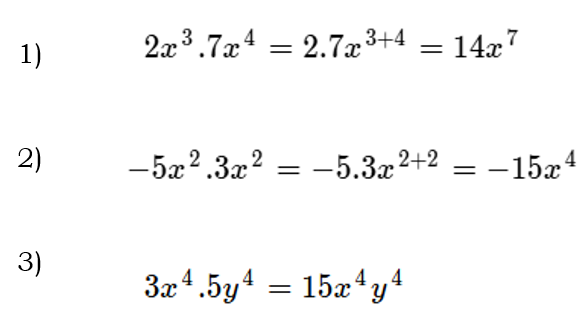
En el tercer ejemplo no se debe sumar los exponentes ya que ambas variables x e y no son semejantes, entonces la operación queda indicada.
A continuación, lo podremos realizar directamente así:
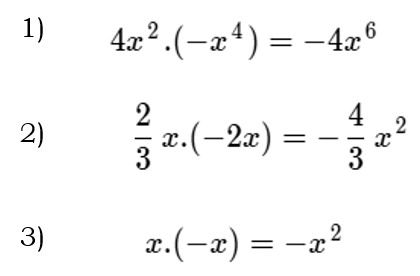
Ahora queremos multiplicar un monomio por un binomio:
Esto es:
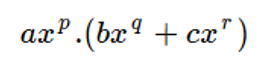
Aquí aplicamos propiedad distributiva de la multiplicación con respecto a la adición, esta propiedad nos dice que, en estos casos, se distribuye el factor con respecto a los sumandos.
Esto es:
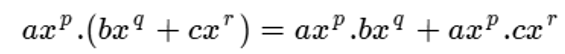
A continuación, algunos ejemplos:
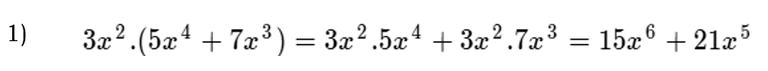
Podemos hacerlo más directo así:
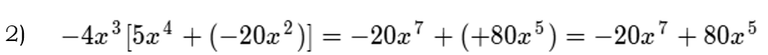
Pero, lo podemos, aún, hacer más directo así:
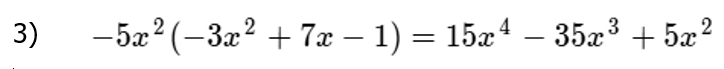
Nota:
Observe que en el tercer ejemplo se está multiplicando un monomio por un trinomio (polinomio de tres términos) y el resultado nos da un trinomio cuyo grado es la suma de los grados de los factores.
Aquí tendremos un ejemplo donde aplicaremos doble propiedad distributiva:
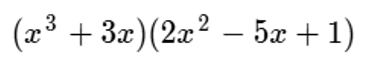
He aquí el desarrollo.
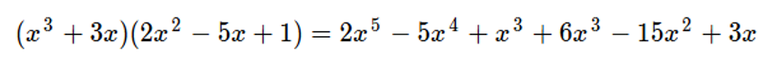
Luego reduciremos términos semejantes:
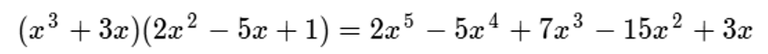
Conclusiones
Para multiplicar polinomios debes tener claro que un polinomio es igual a la suma de monomios de diferente grado; y que, si vas a multiplicar polinomios debes aplicar la propiedad distributiva de la multiplicación con respecto a la adición de polinomios y luego reducir términos semejantes; de esta manera, obtendrás otro polinomio cuyo grado va a ser igual a la suma de los grados de los factores.
Ahora vamos a tratar los PRODUCTOS NOTABLES como un caso especial de la multiplicación de polinomios.
Como lo dice su nombre, producto es el resultado de una multiplicación, es decir que cuando nos dicen productos notables estamos tratando con unas multiplicaciones especiales.
Veamos la siguiente expresión:
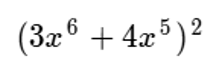
¿Se trata de una potenciación?
El lector se dará cuenta de que sí, estamos frente a una potenciación.
En tal sentido, entonces:
¿Cuál es la base de esa potenciación?
¿Cuántas veces ha de multiplicarse la base por si misma?
¿Cuál es la potencia o resultado de esa potenciación?
Las respuestas a estas preguntas son las siguientes:
La base de esa potenciación es:
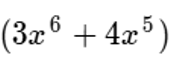
La base habrá de multiplicarse por sí misma dos (2) veces ya que el exponente es 2.
Así:
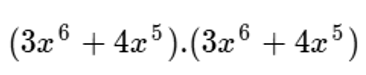
La potencia es el resultado de la multiplicación de la base por si misma dos veces, en este caso, como explicamos antes, usaremos propiedad distributiva.
Así:
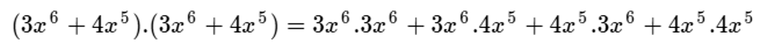
Luego, efectuamos las multiplicaciones indicadas:
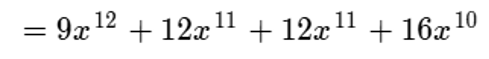
Reducimos términos semejantes:
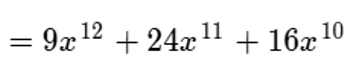
Lo cual corresponde al resultado de la potenciación.
Dejamos al lector para que desarrolle el siguiente producto siguiendo los pasos anteriores.
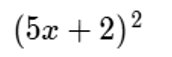
Ahora vamos a desarrollar un algoritmo que nos permita obtener estos resultados de manera directa:
Comencemos por desarrollar el siguiente producto:
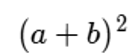
Como ya hemos explicado antes, se trata de multiplicar la base por sí misma, en este caso, dos veces.
Esto es:
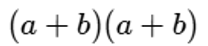
Atendiendo a las explicaciones anteriores, el lector podrá desarrollar por sí mismo este producto.
Este es el resultado:
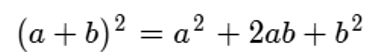
Esta regla o modelo va a ser muy útil por cuanto nos ahorra una cantidad considerable de procedimientos para llegar al resultado deseado.
Apliquemos esta fórmula (modelo) en el ejercicio propuesto al lector anteriormente:
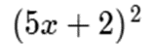
De acurdo a su forma, podemos afirmar que:
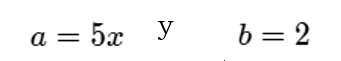
De manera que:
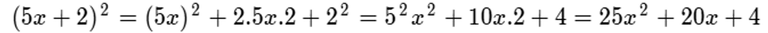
Otro ejemplo, vamos a aplicar este procedimiento en esta expresión:
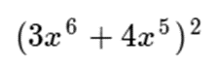
Haciendo analogías, podemos afirmar que:
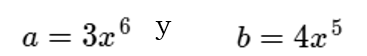
Aplicamos, digámoslo así, “La fórmula”.
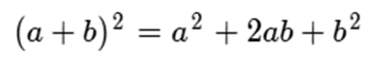
De tal forma que:
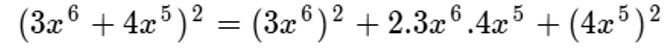
Si desarrollamos los resultados parciales directamente aplicando debidamente las propiedades de las operaciones, obtendremos el resultado final así:
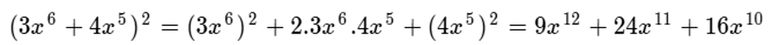
Ahora nos preguntamos:
Cómo se desarrolla el Producto Notable:
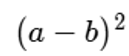
Se puede deducir fácilmente que este producto se desarrolla así:
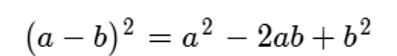
Entendiendo este procedimiento podemos desarrollar cualquier producto notable.
Desarrollemos:
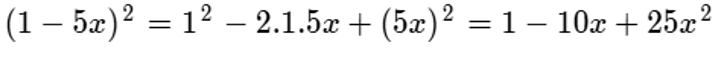
Otro ejemplo de este tipo de producto:
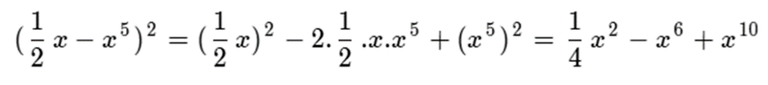
Siguiendo los mismos procedimientos utilizados, el lector podrá desarrollar los siguientes productos notables:
Un binomio por su conjugada:
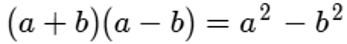
Aquí tenemos un ejemplo del producto de conjugadas:
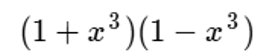
Apliquemos el algoritmo que le corresponde a este caso con:
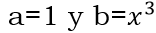
Así:
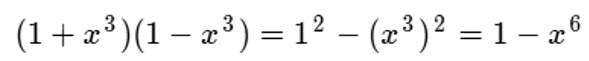
Pasemos a otro tipo de producto, se trata del:
Binomio al cubo:
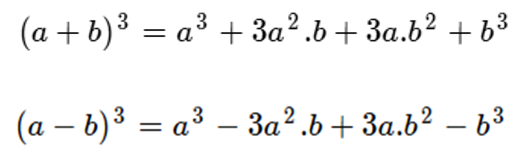
Aquí tenemos un ejemplo de este producto:
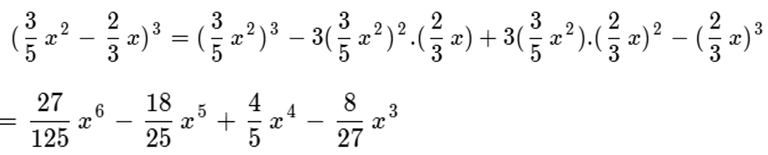
Le proponemos al lector realizar este ejercicio, pero, con signo positivo.
Esto es:
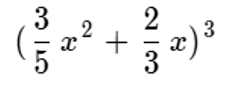
Continuando con los productos notables, también se puede presentar el siguiente:
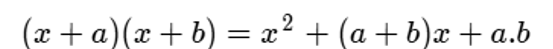
A continuación, un ejemplo:
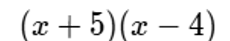
En este ejemplo a=5 y b=-4
Entonces:
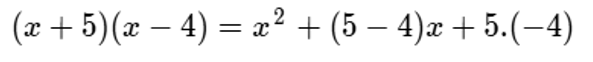
El resultado final es el siguiente:

Resumiendo, estos son los Productos Notables:
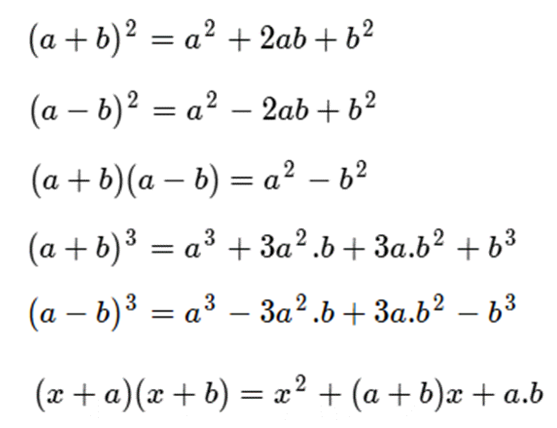
Finalmente, vamos a dejar algunos ejercicios propuestos al lector:
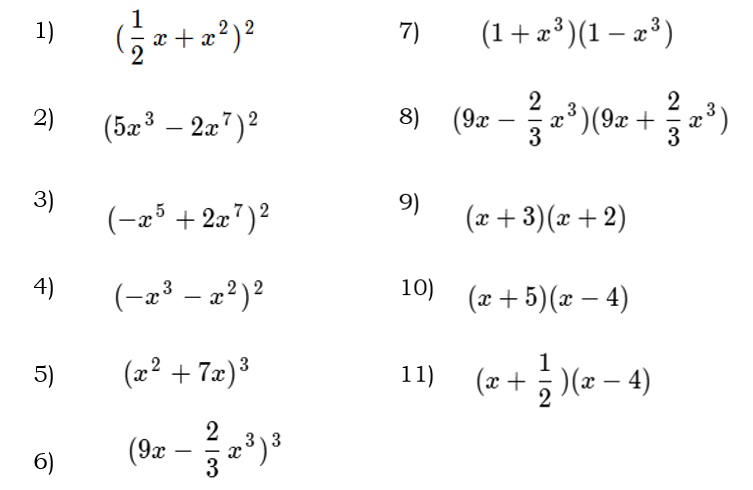
Créditos.
El contenido del post es totalmente original de la autora.
La imagen fue elaborada con la ayuda de Canva.
Se usó TeX equation editor (Mathematical Formulas).
¡Felicitaciones!
1. Invierte en el PROYECTO ENTROPÍA y recibe ganancias semanalmente. Entra aquí para más información.
3. Suscríbete a nuestra COMUNIDADEntra aquí para más información sobre nuestro trail., apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática.
4. Creación de cuentas nuevas de Hive aquí.
5. Visita nuestro canal de Youtube.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA