Un cordial saludo a la comunidad científica de la blockchain de HIVE, especialmente a la familia de StemSocial. Como Ingeniero Civil, uno de los temas que me apasionan es el relativo a los suelos, puesto que toda estructura civil yace sobre este material, por lo que su estudio cobra gran relevancia puesto que de allí surge la información para el proyecto de cimentaciones. En torno a estos estudios, en las referencias 01,02,03,04,05 he abordado el ensayo de consolidación unidimensional de los suelos con un enfoque practico y experimental, cuyo objetivo era estimar los asentamientos diferidos en el tiempo (de allí a que el suelo de interés sean las arcillas) por medio de una serie de ecuaciones que se muestran en el siguiente esquema conceptual, en el que se resumen al mismo tiempo los contenidos a estudiar:
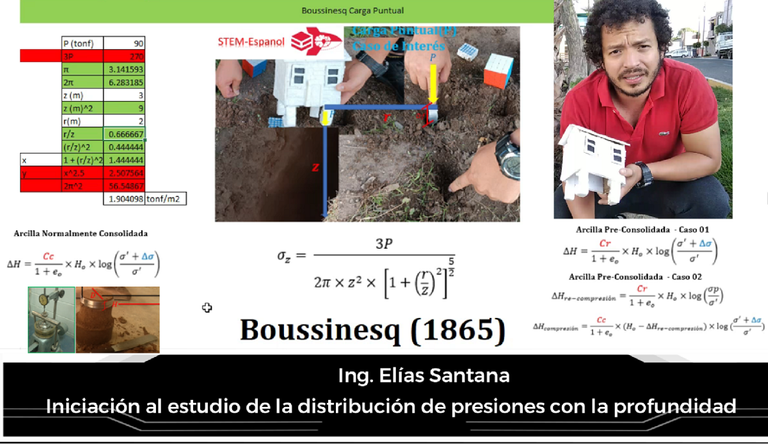
El término resultado en color azul en cada una de estas ecuaciones obedece al estudio de la distribución de las presiones en los suelos y cómo las mismas varían con la profundidad. Y es que cuando se aplica una carga al suelo, por ejemplo, la que proviene de la construcción de un edificio, es necesario determinar el esfuerzo que esto transmite sobre el estrato de interés, que para fines prácticos siguiendo lo expuesto en las referencias anteriormente citadas estaremos enfocándonos a ese suelo arcilloso, suelo en el que el fenómeno de consolidación cobra importancia, dejando en claro que los conocimientos acá expuestos aplican a cualquier tipo de suelo.

Esto que sobre sale del modelo a escala de la casa viene a representar esa parte de la columna que va enterrada a una determinada profundidad de desplante “Df” y que se apoya en la zapata, ese enmallado de acero que muchas veces apreciamos cuando están construyendo una casa y que viene a materializar una especie de ampliación del área de contacto “A” de la columna con el suelo de fundación, la cual mientras mayor sea incidirá en la disminución de los esfuerzos de contacto, guiándonos por esta simple ecuación vemos que “A” está en el denominador:
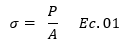
Delimitaremos este estudio con fines netamente didácticos a considerar como única fuerza que llega a esta parte de la fundación a una carga puntual P, simplificando el cálculo de presión de contacto de esta manera a la ecuación anteriormente señalada. Si queremos rigurosidad en el cálculo es necesario recurrir a modelos matemáticos que nos permitan estimar la presión de contacto, donde se tomen en cuenta las diversas fuerzas y momentos que la estructura transmite, este es un tema fascinante de la interacción suelo-estructura que en próximas publicaciones abordaré. Volviendo a lo que nos ocupa, si imaginamos el estrato de arcilla a unos 5 m de profundidad, entonces surge la siguiente interrogante de interés:
¿Cuánto sería el esfuerzo a esa profundidad? ¿Crees que es el mismo esfuerzo que el del plano de contacto?
Y en torno a esta pregunta se desencadena el desarrollo de muchas teorías y técnicas, entre las que más resaltan Boussinesq, Fadum, Newmark, Bulbo de Presiones, entre otras. Al responder esta interrogante, tendríamos ya todos los datos de las ecuaciones que permiten estimar asentamientos por consolidación unidimensional en las arcillas, las mismas se resumen a continuación:

Y hacia allá estará enfocada el desarrollo de esta serie temática, en abordar los diversos métodos que nos permitirán encontrar “Δσ”, y atendiendo al título de la publicación para iniciar con este estudio es importante tener claro ciertas suposiciones que los creadores de estos métodos tuvieron que asumir para poder desarrollar sus teorías. Porque el suelo es un material tan complejo, que es necesario recurrir a planteamientos que de algún modo u otro busquen idealizarlo como un material fácil de abordar. Y es por eso que al tópico que sigue lleva como título:
Mentiras que creemos del suelo con total conveniencia: isotrópico, elástico, homogéneo, semi -infinito
¿Es isotrópico el suelo?
El término Isotropía describe una constante en las propiedades del material indistintamente en la dirección que se le analice o estudie. En el suelo esto no es así, según Crespo Villalaz (2008)
“…lo suelos son formaciones naturales que se han consolidado, y por lo tanto las propiedades de resistencia en dirección horizontal son diferentes a las de resistencia en dirección vertical”Considerar al suelo como anisotrópico haría complicado el desarrollo de teorías que buscan estudiar la distribución de las presiones con la profundidad, de allí a que simplemente se le considere un material Isotrópico.

¿Es elástico el suelo?
Para comprender el concepto de elástico imaginemos una liga, al aplicar una carga se deforma, pero al retirar esta carga, la liga recupera su forma original. Un suelo no tiene este comportamiento, en el caso particular de las arcillas por citar un ejemplo, una vez que aplicamos las cargas se deforma y al removerla el suelo en cuestión intenta recuperar su forma original pero no lo logra quedando deformaciones permanentes, presentando un comportamiento plástico. Es tan complejo el material suelo que lo encasillan en un comportamiento “elasto-plástico”. Considerar al suelo de esta manera, evidentemente que complicaría las cosas en el establecimiento de las ecuaciones que nos permitan encontrar “Δσ”, por eso simplemente se considera Elástico, donde aplica la Ley de Hooke, es decir, los esfuerzos son proporcionales a las deformaciones.

¿Es homogéneo el suelo?
Una imagen dice más que mil palabras, en efecto un suelo en particular no es perfectamente homogéneo, en el interior de su masa podemos encontrar mezclas con otros tipos de suelo, o incluso pequeños fragmentos de roca, al mismo tiempo concentraciones de agua que definirían la humedad del suelo en cuestión, y de otras variables como el grado de saturación. En sí por naturaleza el suelo es heterogéneo, el simple hecho de provenir de la descomposición mecánica y química de la roca le confiere esta característica. No obstante los teóricos lo idealizan como homogéneo para poder avanzar en el planteamiento de las teorías que estudian las presiones en la masa del suelo.

En líneas generales los teóricos idealizaron al suelo como un material que es Isotrópico, Elástico y Homogéneo, con lo cual es factible calcular la distribución de presiones que ocurren en el interior de su masa, producto de una carga externa aplicada como la que se muestra en la imagen de presentación. Unas de las primeras ecuaciones que se desarrolló en pro de esta solución fue la planteada por Boussinesq (1865), la cual es:

Una ecuación bastante popular entre los estudiosos de Mecánica de Suelos que buscamos entender la interacción de este con las cargas que transmite la estructura y que viene a definir una especie de patrón o de base para los diversos casos de estudio que nos podamos encontrar, porque en esencia lo que queremos determinar es cómo ese esfuerzo que se aplica en el plano de contacto se distribuye con la profundidad, en la imagen que sigue podemos apreciar las principales variables involucradas que inciden en este cálculo:

El término “z” hace referencia a la profundidad de interés, normalmente evaluamos en diversas profundidades, de pronto podemos colocar nuestra fundación en un estrato arenoso arcilloso, pero puede que con la profundidad la estratigrafía cambie y tengamos por ejemplo a 3 m de profundidad arcillas que pueden experimentar consolidación, y entonces conviene saber cuanto esfuerzo está llegando a esta profundidad. Si planteamos que la carga transmitida por esa columna es por ejemplo de P=100 T, con un r= 0 m, es decir, nos interesa saber cómo esta se distribuye a partir de su punto de aplicación en relación a la profundidad. En algunos casos puede resultar de interés saber cómo es esa distribución de esfuerzos con la profundidad, pero a una cierta distancia desde donde se aplicó la carga, en ese sentido el valor de “r” ya no sería cero, por ejemplo podemos tener un r=1.00 m. Sustituyendo los datos presentados, por ejemplo para el caso de r= 0 tenemos:
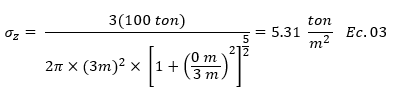
En el caso de que queramos ver como es la distribución de esfuerzos a una distancia horizontal de 1 m “r=1.00 m” con respecto al punto donde se aplicó la carga, el cálculo es el que sigue:
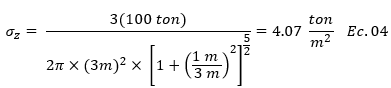
Vale destacar que esta ecuación solamente estudia el comportamiento que tendría un carga puntual en contacto con el suelo, es el caso más simple, pero que sirve para darnos una idea en términos prácticos de lo que buscamos con la aplicación de estos cálculos, es decir , ese valor que hemos obtenido es el “Δσ” requerido en las ecuaciones de consolidación unidimensional presentadas en la imagen inicial. Ahora bien, en cuanto al tema de distribución de presiones tenemos que existen ecuaciones que se pueden adaptar más al problema que tenemos, en el caso de la imagen anterior esa columna se conecta a una zapata, entonces veo oportuno trabajar con ecuaciones de distribución de presiones con la profundidad que directamente se enfoquen presiones de contacto, esto invita por lo tanto a estudiar los diversos aportes que teóricos han hecho hacia este tema, y así contrastar resultados. En torno a estas ideas estaré trabajando en una próxima publicación, por lo que ahora nos ocupa estas conclusiones que a continuación presento resumen las principales enseñanzas que esta publicación buscó:
Conclusiones de Importancia
01.- Consideramos que el suelo es un material isotrópico, homogéneo y elástico, para dar paso a diversas ecuaciones que permiten encontrar los esfuerzos en el interior de la masa de este material.
02.-Existen diversos casos de carga que pueden ir desde puntual, lineal, distribuida o aquellos modelos que se basan en estimar la presión de contacto y ver cómo esta se distribuye, hacia este campo estaremos centrando la atención en futuras publicaciones.
03.-Cononocer la forma como las presiones en el suelo se distribuyen es una labor muy importante en el diseño de nuestras cimentaciones, dado que podemos tener nociones del esfuerzo que está llegando a un determinado estrato, lo cual influirá en los asentamientos que este pueda experimentar y a partir de allí tomar las medidas necesarias.
Estos temas de la ingeniería en muchas ocasiones resultan engorrosos de explicar, es para mi un reto transmitir estos conocimientos de la forma más didáctica posible, con la intención de que nuestros estudiantes se enamoren de estos temas fascinantes de la Mecánica de Suelos. Espero la lectura de esta publicación haya sido de tu agrado, nos leemos en una próxima oportunidad y no dejes de ver el recurso audiovisual del comienzo donde a través de ejemplos prácticos, complemento las ideas expuestas en esta publicación. Escribió para ustedes:
@eliaschess333
Créditos de la producción audio-visual:
@normacanaza asistente en la grabación del video y toma de fotografías
El fondo musical empleado es de uso libre, extraído del portal de pixabay: https://pixabay.com/es/music/late-jazzy-abstract-beat-11254/
El video fue editado con Filmora 11
El ejemplo práctico fue desarrollado en la herramienta Microsoft Excel, realizando las capturas de pantallas necesarias para ilustrar la publicación
En el proceso de edición de imágenes, se usaron las herramientas Paint y Microsoft PowerPoint
El logo de #Stem-Espanol es cortesía de la comunidad
Las imágenes de suelo, consolidometro son de mi propiedad, representan para de mi experiencia como profesor universitario en la unidad curricular Mecánica de Suelos, de la Universidad Nacional Experimental Francisco de Miranda, Venezuela.
Bibliografía consultada:
01.- BADILLO J. Y RODRÍGUEZ R. 2007. MECÁNICA DE SUELOS TOMO I. FUNDAMENTOS DE LA MECÁNICA DE SUELOS. EDITORIAL LIMUSA S.A. GRUPO NORIEGA EDITORES00.
02.-CRESPO VILLALAZ. 2008. MECÁNICA DE SUELOS Y CIMENTACIONES. EDITORIAL LIMUSA.. SEXTA EDICIÓN
03.-BRAJA M. DAS.2001 FUNDAMENTOS DE INGENIERÍA GEOTÉCNICA. THOMSON&LEARNING.
Lecturas Recomendadas:
Referencia 01: ABORDAJE DIDÁCTICO DEL FENÓMENO DE CONSOLIDACIÓN UNIDIMENSIONAL DE LOS SUELOS DESDE UN ENFOQUE EXPERIMENTAL. PARTE I #EL SUELO ES ALGO MÁS DE LO QUE PISAMOS. Disponible en: https://hive.blog/hive-196387/@eliaschess333/arbodaje-did-ctico-del-fen-meno-de-consolidaci-n-u-1591702845
Referencia 02: ABORDAJE DIDÁCTICO DEL FENÓMENO DE CONSOLIDACIÓN UNIDIMENSIONAL DE LOS SUELOS DESDE UN ENFOQUE EXPERIMENTAL. PARTE II #EL SUELO ES ALGO MÁS DE LO QUE PISAMOS. Disponible en: https://hive.blog/hive-196387/@eliaschess333/ekocigvy
Referencia 03: ABORDAJE DIDÁCTICO DEL FENÓMENO DE CONSOLIDACIÓN UNIDIMENSIONAL DE LOS SUELOS DESDE UN ENFOQUE EXPERIMENTAL. PARTE III #EL SUELO ES ALGO MÁS DE LO QUE PISAMOS. Disponible en: https://hive.blog/hive-196387/@eliaschess333/fioocwjx
Referencia 04: ABORDAJE DIDÁCTICO DEL FENÓMENO DE CONSOLIDACIÓN UNIDIMENSIONAL DE LOS SUELOS DESDE UN ENFOQUE EXPERIMENTAL. PARTE IV #EL SUELO ES ALGO MÁS DE LO QUE PISAMOS. Disponible en: https://hive.blog/hive-196387/@eliaschess333/abordaje-didactico-del-fenomeno-de-consolidacion-unidimensional-de-los-suelos-desde-un-enfoque-experimental-parte-iv-el-suelo-es
Referencia 05: ABORDAJE DIDÁCTICO DEL FENÓMENO DE CONSOLIDACIÓN UNIDIMENSIONAL DE LOS SUELOS DESDE UN ENFOQUE EXPERIMENTAL. PARTE V #EL SUELO ES ALGO MÁS DE LO QUE PISAMOS. Disponible en: https://hive.blog/hive-196387/@eliaschess333/abordaje-didactico-del-fenomeno-de-consolidacion-unidimensional-de-los-suelos-desde-un-enfoque-experimental-parte-v-el-suelo-es
▶️ 3Speak
Buen post mi rey 👍 que Dios te llene de mucha creatividad, inventiva y sabiduría 😃te amo mi rey 😍😘
Gracias mi reina, gracias por apoyarme en el modelo a escala y las tomas del vídeo, te dedico este post, TE AMO❤️❤️❤️
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.
Thanks for the support!
Your content has been voted as a part of Encouragement program. Keep up the good work!
Use Ecency daily to boost your growth on platform!
Support Ecency
Vote for new Proposal
Delegate HP and earn more
Thanks for the support!