La ecuación de Clapeyron es una conocida relación matemática empleada para describir los cambios de presión y temperatura que ocurren durante la transición de materia entre dos fases que se encuentran en equilibrio; siendo aplicable a las transiciones de fase de primer orden en sistemas de un solo componente. Esta ecuación propuesta en 1834 por el físico E. Clapeyron, constituye uno de los conceptos fundamentales para el estudio de los cambios de fase y es una de las primeras grandes contribuciones de la fisicoquímica.
pizarrón y la olla son de dominio público.La ecuación de Clapeyron es una importante relación para el estudio de los cambios de fase en sustancias puras. Fuente: @emiliomoron, la imagen del
La ecuación de Clapeyron
Benoit Pierre Emile Clapeyron (1799-1864) fue un ingeniero francés que se dedicó al estudio de del comportamiento físico de gases y vapores durante la década de 1830, y fue capaz de proponer una relación que describe los cambios de entalpía de la transición de fase de líquido a vapor en términos de la presión, la temperatura y el volumen específico, aportando de esta forma una ecuación que permite calcular los cambios de entalpías en términos de propiedades medibles directamente, siendo una de las primeras ecuaciones que permitía hacerlo para la época.
La ecuación proporciona la pendiente dP/dT de las líneas de equilibrio entre dos fases en los diagramas P-T para sustancias puras. Para deducirla consideremos que los puntos 1 y 2 sobre la línea de equilibrio de la siguiente gráfica se encuentran infinitamente próximos, esta línea representa el equilibrio entre las fases indicadas como α y β, que pudiera ser cualquier equilibrio; sólido-líquido, líquido-vapor, sólido-vapor o sólido-líquido.
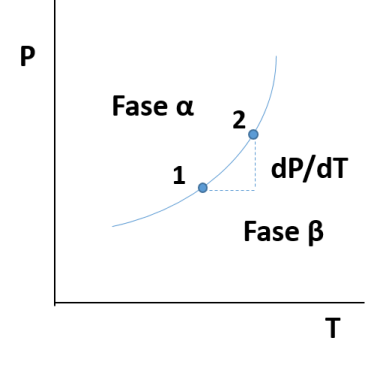
Representación de una línea de equilibrio. Fuente: @emiliomoron.
Ya que la condición para que exista un equilibrio entre dos fases es que los potenciales químicos de la sustancia en ambas fases sea el mismo (μα=μβ), y como para una sustancia pura μ es igual a Gm, entonces podemos decir en este caso que Gα = Gβ en cualquier punto sobre la línea de equilibrio.
Ahora bien, para un sistema monofásico de una sustancia pura se tiene que:
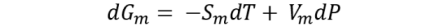
Si consideramos que al pasar del punto 1 al punto 2 se produce un cambio infinitesimal en la energía de Gibbs molar de las fases α y β, se puede escribir que:
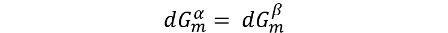
Por lo tanto,
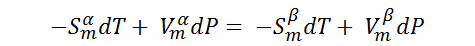
Donde dT y dP son los cambios infinitesimales producidos en la temperatura y la presión al cambiar las condiciones de equilibrio del punto 1 al punto 2. Reordenando la ecuación nos queda:
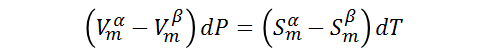
Tal que:
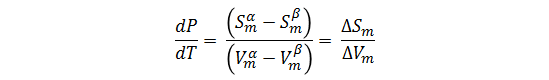
Donde ΔS y ΔV son los cambios de entropía y volumen que ocurren debido a la transición de fase.
En un cambio de fase reversible se puede tomar ΔS=ΔH/T, y al sustituir en la ecuación anterior, obtenemos la ecuación de Clapeyron:
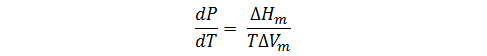
Esta ecuación proporciona la relación entre los cambios de presión que deben acompañar a los cambios de temperatura en un sistema de dos fases que se encuentra en equilibrio.
Formas integradas de la ecuación de Clapeyron
Equilibrio líquido-vapor y sólido-vapor
Cuando existe un equilibrio entre una fase vapor y una fase líquida o con una sólida, el Vm,gas es mucho mayor que el Vm,líquido o el Vm,sólido; por lo que se puede decir que ΔVm ≈ ΔVm,gas, y si además, se considera que el gas se comporta de forma aproximada a la idealidad, entonces ΔVm,gas ≈ RT/P. Si utilizamos estas dos suposiciones podemos escribir la ecuación de Clapeyron de la siguiente forma:
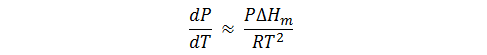
Y ya que dP/P es igual a d lnP,
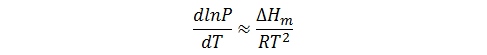
A la ecuación anterior se le denomina ecuación de Clausius-Clapeyron en la mayoría de los textos de fisicoquímica, aunque en muchos documentos se le denomina del mismo modo a la forma general de la ecuación de Clapeyron.
Si suponemos que la ΔHm permanece constante a la largo de la línea de equilibrio, la integración de la ecuación anterior da:
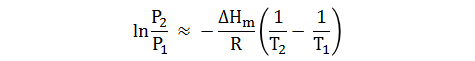
Con esta ecuación, conociendo el valor de ΔH, se puede determinar la presión de vapor a cierta temperatura, a partir de una presión de vapor conocida.
Equilibrio sólido-líquido
La ecuación de Clausius-Clapeyron no es aplicable si se trata de un equilibrio sólido-líquido, ya que durante la fusión el cambio de volumen si es influyente. Pero si consideramos que ΔS = ΔH/T, entonces podemos escribir la ecuación de Clapeyron de la siguiente forma:
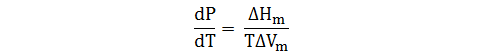
Si reordenamos la expresión, e integramos tomando la suposición que tanto ΔS y ΔV son aproximadamente constantes, la ecuación nos queda como:
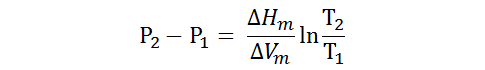
La forma de la ecuación anterior se utiliza para el cálculo de la presión o temperatura de equilibrio de fases condensadas.
Ejemplos de aplicación de la ecuación de
- El punto de ebullición normal del agua es de 100 °C, y a esta temperatura el ΔHvap es igual a 40,66 J/mol.K, ¿hasta qué valor sería necesario aumentar la presión para que el agua hierva a 120 °C?
En este caso vemos que se habla de cambios en la temperatura de ebullición, por lo que se utilizará la forma integrada de la ecuación de Clapeyron, o ecuación Clausius-Clapeyron, para el tratamiento del equilibrio líquido-vapor.

Para los equilibrios líquido-vapor se emplea la ecuación de Clausius-Clapeyron. Fuente: imagen de la olla es de pixabay.com.
Y para resolver el problema debemos estimar la presión de vapor del agua, digamos que esta es P2 para una temperatura de 120 °C (la cual sería T2). Y sabiendo que la presión de vapor del agua a 100 °C es 760 torr, estos serían los datos que necesitamos para definir el estado 1.
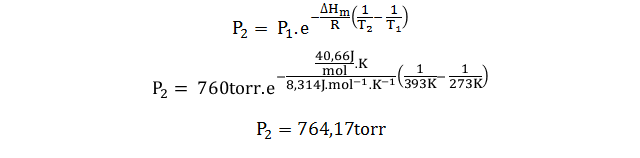
Por lo que sería necesario un aumento de 4,17 torr para elevar la temperatura de ebullición del agua hasta 120 °C.
- Calcule el punto de fusión del hielo a 100 atm sabiendo que para 1 g de hielo el ΔHfus es 79,7 cal (la densidad del hielo y el agua a 0 °C y 1 atm es 0,917 g/cm3 y 1,000 g/cm3 respectivamente).
En este caso se trata de un equilibrio sólido-líquido, por lo cual se utiliza la forma integrada de la ecuación de Clapeyron.

Para los equilibrios sólido-líquido se emplea la forma general de la ecuación de Clapeyron. Fuente: @emiliomoron.
Las densidades se utilizan para determinar el cambio en el volumen, para un gramo de hielo es:
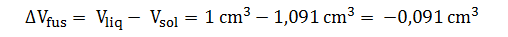
Si consideremos el estado 1 como el punto de fusión normal, tenemos:
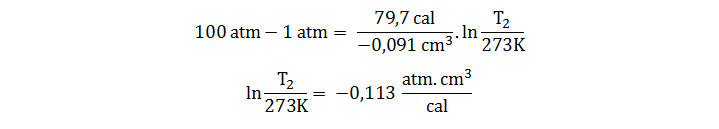
Para proseguir utilizamos dos valores de la contante R para ajustar las unidades:
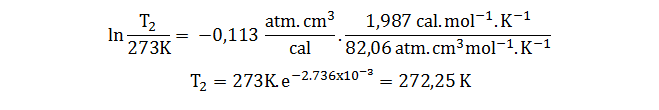
Es decir, que el aumento de la presión ha hecho descender la temperatura de fusión del hielo en aproximadamente 0,7 grados.
Conclusión
Como vemos, la ecuación de Clapeyron expresa que al modificar la presión en un sistema bifásico en equilibrio, la temperatura también se verá afectada, y esta sencilla relación nos permite estimar la presión o la temperatura de una nueva condición de equilibrio partiendo de una conocida, solo debemos aplicar la ecuación de acuerdo al tipo de equilibrio que presentado.
Bueno amigos espero les haya gustado la información sobre esta útil e importante ecuación. ¡Hasta la próxima!
Referencias
Robert T. Balmer (2011). Modern Engineering Thermodynamics. Capitulo 11, pag. 361-404. Elsevier Inc.
Levine, I. (2004). Fisicoquímica. 5ta edición. McGrawHill.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.