So far in my previous post, we have assumed that there is no friction in our oscillating systems. However, in reality, this can never happen – there will always be some friction, causing energy to be lost from the system.
The total energy of a vibrating system depends on the square of the amplitude. If energy is removed from the system, the amplitude of vibration is reduced. How rapidly this happens depends on the amount of friction, which causes what is known as damping.
Damping, causing a reduction in the amplitude of vibration, is often an advantage. With light damping, the oscillations gradually reduce in amplitude but take a long time to disappear. With very heavy damping, the system does not oscillate but returns to its equilibrium position very slowly. With critical damping, the amount of friction is such that the system returns as quickly as possible to equilibrium without ‘overshooting’ in the opposite direction. The time for this to happen is approximately a quarter of the period for free oscillation of the system.
Smoothing out a bumpy ride
Car suspensions are fitted with springs and shock absorbers to damp out the vibrations of a moving car. The shock absorbers are pistons moving up and down in a viscous fluid (usually an oil). They are attached to the car chassis. Without the shock absorbers, the car would bounce up and down repeatedly on the springs.

The amount of damping is set by the dimensions and materials of the spring and absorber. Car suspensions need to be slightly less than critically damped. If there is too much damping, then when the system has responded to a bump or rut in the road it does not return to its equilibrium position in time to respond to the next bump or rut. If the damping is too light, the passengers experience a lot of oscillations before the system recovers. When shock absorbers become worn, the ride of a car becomes bouncy and rather uncomfortable.
FORCED OSCILLATIONS AND RESONANCE
If the vibrating system is losing energy, it is possible to replace the energy or even increase the total energy by applying a force to the system periodically and in the correct direction. If the frequency of the applied force is the same as the natural frequency of the system, the amplitude of vibration builds up.
Think about pushing a child on a swing. You time your pushes to coincide with the natural oscillation, but have to be careful not to push too much or too often as this would cause the amplitude to get too large and the child could fall off.
It is often necessary to prevent vibrations building up in mechanical systems. When the applied force has the same periodic frequency as the natural frequency of the system, we say resonance occurs. When this happens, a large amount of energy is given by the force to the system. (You may have felt intense vibrations when in a car next to a large vehicle with a powerful engine running.)
In a spectacular case of resonance, vibrations set up in the Tacoma Narrows Bridge by strong winds led to its famous collapse. The amplitude of vibration of the bridge became larger and larger until the bridge broke up.

Soldiers marching across a bridge can make it resonate. In 1850, 200 soldiers marching in step across a bridge in Angers, France, lost their lives when the resonance between the frequency of their steps and the natural frequency of the bridge caused the bridge to collapse. To avoid this, soldiers break step across bridges. It has proved necessary to damp out the oscillations set up by pedestrians when they walked across the Millennium Bridge built over the River Thames in central London.
In a car, you get uncomfortable vibrations due to resonance at particular speeds of either the engine or the vehicle itself. If resonance were set up in a turbine or a jet engine, it is possible that the engine would disintegrate. So we can see that it is important to avoid resonance in structures and vehicles.
Damping prevents the build-up of amplitude. The amplitude of vibration of an oscillating system varies with the frequency of the driving force and also damping affects the resonance curves. When the frequency of the driving force equals the natural frequency of the system being driven, the oscillations build up and can become totally uncontrollable.
Resonance can be used to advantage, however, and not only in pushing swings. Resonance is used to amplify the desired frequency when tuning an electrical circuit.
COUPLED PENDULUMS
If two identical oscillators can interact then they will exchange energy, just as the soldiers marching in Angers exchanged energy with the bridge with disastrous results.
A pair of pendulums of the same length can be connected to a common support and set swinging, as shown in the figure below. It helps to lightly link the pendulums, but often enough energy can pass through the support itself. When pendulum 1 is set swinging, its energy gradually leaks through to pendulum 2 until all energy is transferred and it is stationary. Pendulum 2 has now achieved maximum amplitude and starts to pass the energy back to pendulum 1; and so on.
As a variation of this demonstration, the so-called Barton’s pendulums are suspended from one length of string, as in the figure. There is one heavy pendulum (the driver), and a series of pendulums with bobs of smaller equal mass. The lengths of the pendulums differ but one is of equal length to the driver pendulum. It is this one which starts to vibrate with the largest amplitude.

WAVES AS OSCILLATIONS
We have seen that oscillations are periodic. We know that waves are also periodic. Clearly there is a relationship between the two. In fact, an oscillating system can be used to set up waves in a mechanical system. Once the waves have been set off, they travel through the spring or other medium for long distances until the energy is dissipated.
There are different types of waves. Some need a substance to pass through – these are called mechanical waves. Such waves displace (i.e. move) the material which they pass through. However, there is no net motion of the material through which the waves travel, as displaced material has moved back into its original position by the time the wave has passed through.
Examples of mechanical waves are seismic waves in the Earth, water waves on the surface of ponds and oceans, and sound waves through air. Seismic waves are usually set up by earthquakes but can be caused by nuclear explosions. The speed with which they travel depends on the medium and the type of wave.
There are other waves, called electromagnetic waves, which require no medium to travel in. These waves were explained in one of my previous posts here and here
TRANSVERSE AND LONGITUDINAL WAVES
Mechanical waves can be divided into transverse or longitudinal according to their method of travelling. We can demonstrate the two types of wave by using a slinky spring. The transverse wave is observed when the coils move at perpendicular i.e at right angles to the direction of the wave's motion, with the movement along the length of the slinky. To produce a transverse wave, the slinky is rested on a flat surface and one end is moved from side to side, setting up the oscillation and hence the travelling wave.
The end of the slinky can also be moved in and out along its axis. The coils undergo compression, followed by rarefaction when the coils open out. Displacement of the coils is now along the axis of the spring; this is a longitudinal wave.
TRAVELLING AND STATIONARY WAVES
When we start a wave in the slinky, either transverse or longitudinal, we can watch it travel from one end to the other. Because it progresses along the slinky, it is called a travelling (or alternatively a progressive) wave. However, if the far end of the slinky is fixed, waves are reflected back. These can combine with the next waves which are travelling forwards. At the right combination of frequency and speed, the waves travelling in opposite directions can produce stationary or standing wave. In this chapter we shall consider both types.
SETTING UP TRAVELLING WAVES
In general, waves spread out once they are generated, like the ripples in a pond when a pebble is dropped into it. The spreading of waves, both transverse and longitudinal, is looked at in detail here. Here, we restrict ourselves to setting up linear waves such as along a slinky, in a string or in an organ pipe.
Transverse waves are easier to show, so let us look at transverse waves set up in a stretched string. With care, we can set up a single pulse in the string and watch it travel, as shown below. Although the pulse maintains its shape, its amplitude is likely to decrease as it passes along the string. Such pulses can continue for long distances.
We can also set up in the string a wave train consisting of a number of waves. It too will travel down the string and preserve its shape. Alternatively, by continuing to vibrate one end of the string, we can establish a continuous wave travelling along the string.
There are a number of features of these waves to notice. First, the speed of the pulse, wave train or continuous wave passing down the string is independent of the frequency with which the end is vibrated, and is also independent of the amplitude of the waves established. The speed depends on the nature of the string only. It is because the speed is constant that the shape of the pulse or wave remains the same,
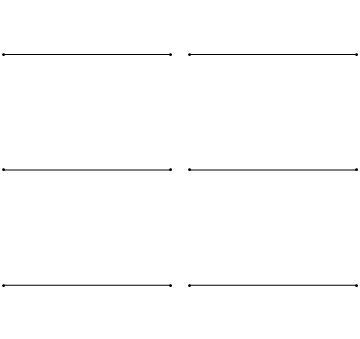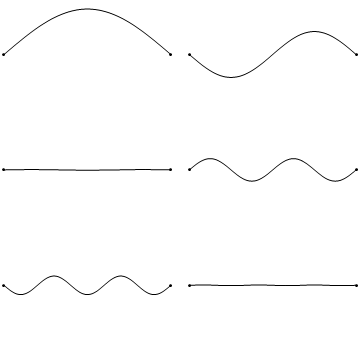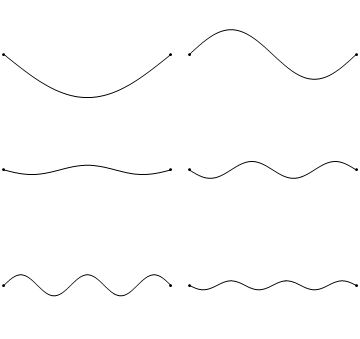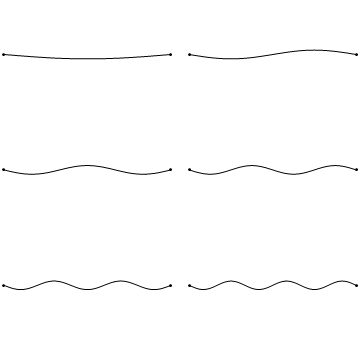
Suppose the wave moves by exactly its own length during a time T, the wave has moved by a single wavelength λ. The velocity of the wave is the distance travelled divided by time and so we have:
V = λ/T
As the time T is the time of travel through one complete oscillation, the wave will have moved from AB to BC and a succeeding wave will have moved into position AB, as shown by the broken line in the drawing. T is the period of vibration. Also, the frequency of vibration f is given by:
F = 1/T
So that we have:
V = λ/T = f × λ
Speed = frequency × wavelength
This simple wave formula applies to all waves. The frequency of the wave is the frequency of vibration used to set up the waves from the end of the string. As the speed is a characteristic of the string, wavelength in a given string will depend on the frequency of the oscillating source.
Another important property of the wave is its amplitude A, which is the maximum displacement of any point on the wave, or any point on the string, from the zero displacement position.
Boat sets up a soliton
A single pulse has been given the special name of soliton. It is not easy to set one up in a string, but the transmission of solitons along optic fibres is important in optical signal communications.
In 1834, John Scott-Russell was walking by the Forth-Clyde canal when he saw a large-scale soliton and wrote this description of it.
'I was observing the motion of a boat which was rapidly drawn along a narrow channel by a pair of horses, when the boat suddenly stopped- not so the mass of water in the channel which it had put in motion; it accumulated round the prow of the vessel in a state of violent agitation, then suddenly leaving it behind, rolled forward with great velocity, assuming the form of a large solitary elevation, a rounded, smooth and well-defined heap of water, which continued its course along the channel apparently without change of form or diminution of speed. I followed it on horseback, and overtook it still rolling on at a rate of some eight or nine miles an hour, preserving its original figure some thirty feet long and a foot to a foot and a half in height. Its height gradually diminished, and after a chase of one or two miles I lost it in the windings of the channel. Such, in the month of August 1834, was my first chance interview with that singular and beautiful phenomenon.’
If one could set up a wave machine across the canal in order to establish continuous waves down the canal of a wavelength comparable with the separation of the canal banks, then these waves would keep going over a long distance without disruption. This is what happens on a much smaller scale when light pulses are sent long distances down a monomode optical fibre.
In my next post, I will explain how to set up stationary waves and the Doppler effect. Till then, I remain my humble self, @emperorhassy.
Thanks for reading.
REFERENCES
https://www.britannica.com/science/damping
https://en.wikipedia.org/wiki/Damping_ratio
https://www.britannica.com/technology/shock-absorber
https://en.wikipedia.org/wiki/Shock_absorber
https://link.springer.com/chapter/10.1007/978-3-319-72314-3_3
https://courses.lumenlearning.com/physics/chapter/16-8-forced-oscillations-and-resonance/
https://www.sciencedirect.com/topics/engineering/forced-oscillation
https://iopscience.iop.org/article/10.1088/0031-9120/45/4/012
https://www.exploratorium.edu/snacks/coupled-resonant-pendulums
http://www.physics.purdue.edu/~jones105/phys42200_Spring2013/notes/Phys42200_Lecture3.pdf
https://www.khanacademy.org/science/physics/mechanical-waves-and-sound
http://minerva.union.edu/newmanj/Physics100/Color,%20Eye,%20&%20Waves/oscillations_and_waves.htm
https://en.wikipedia.org/wiki/Mechanical_wave
https://courses.lumenlearning.com/boundless-physics/chapter/waves/
https://circuitglobe.com/travelling-wave.html
https://phys.libretexts.org/Bookshelves/University_Physics/Book%3A_University_Physics
https://www.sciencedirect.com/topics/engineering/travelling-wave
https://www.researchgate.net/figure/In-the-1830s-the-engineer-John-Scott-Russell-observed-a-strange-wave-on-the-Union-Canal_fig3_240968813
http://maths.straylight.co.uk/archives/256
a beautiful job complimenting you!
!discovery 40
Thanks, @riccc96.
Questo post è stato condiviso e votato all'interno del discord del team curatori di discovery-it Entra nella nostra community! hive-193212
This post was shared and voted inside the discord by the curators team of discovery-it. Join our community! hive-193212
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @steemstem account (for some ROI).
Please consider using the STEMsocial app
app and including @stemsocial as a beneficiary to get a stronger support.
Some interesting phenomenon shown by coupled pendulums.
A great thanks, @rahul.stan.