
The amplitude of the signal going into and out of the amplifier could be measured in volts, and so the amplifier may be described as a voltage amplifier. The output voltage will be bigger than the input voltage: the ratio of the output to the input is called the gain of the amplifier. The gain may be expressed as a number (such as 10 times) or may be measured in decibels (dB).
The decibel
Very often in electronics we wish to compare the relative amplitude of two signals. The signals could be the input to and output from an amplifier, a the ratio could be very large, sometimes as big as millions. For this reason is easier to use a logarithmic scale, as shown in the table below.
| Linear scale, N | 1 | 10 | 100 | 1000 | 10000 | 100000 |
|---|---|---|---|---|---|---|
| Logarithmic scale, log10N | 0 | 1 | 2 | 3 | 4 | 5 |
A unit called the decibel is used. By definition, the ratio of two signals in decibels is:
dB = 20 log10(V2/V1)
Where V1 and V2 are the peak voltages of the two signals. (Although we could as well use the r.m.s. voltages)
EXAMPLE
The input to an amplifier has a peak voltage of 0.2 mV. The output has a peak voltage of 2 V. What is the gain of the amplifier?
ANSWER
Gain = Output voltage / Input voltage = 2 V/0.2 mV = 10 000 times (or × 10 000)
Or, in dB:
Gain = 20 log10(Vout/Vin) = 20 log1010 000 = 20 × 4 = 80 dB
Input and output impedance
When a signal passes into an amplifier, there is a current. The size of the current depends on the signal voltage at any instant, but it also depends on the input impedance of the amplifier. The impedance is measured in ohms.
The signal coming out of the amplifier is also a current and has a voltage (usually both are fluctuating) and is passed into another device or load. In the case of an audio amplifier, the load is usually a loudspeaker. The output of the amplifier behaves as a signal source. The current that this source drives through the load depends on the source voltage, the impedance of the load and the output impedance of the amplifier
It helps to think of the output of the amplifier as a source of alternating e.m.f. with an internal resistance – rather as a battery is made up of a source of e.m.f. ε in series with its internal resistance r.
When the signal source is connected to a load, it operates most efficiently when the load impedance is the same as the output impedance of the amplifier. This is a result of the maximum power theorem.
Impedance: Capacitors and inductors have reactance in a.c. circuits. We treat electronic circuits as a.c. circuits, as the signals they process are often alternating. The combination of resistance and reactance is called impedance. Like resistance and reactance, it is measured in ohms, and like reactance it depends on frequency.
Impedance, Z, is given by: Z = √(R2 + X2) where R is resistance and X is reactance.
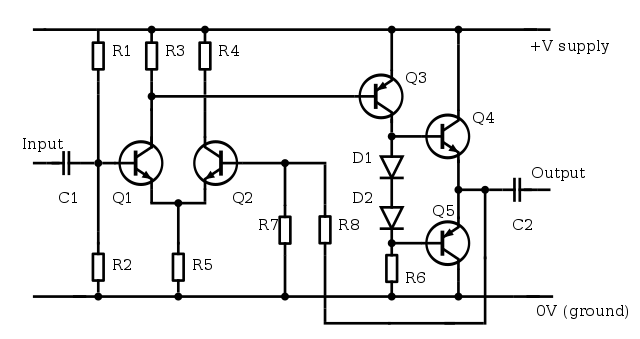
Maximum power theorem
This is a useful idea from d.c. circuits that help in the design of efficient electronic systems. How does the energy transferred from a battery to a load depend on the resistance of the load? Consider the two extremes of the load that is, zero resistance and very high (infinite) resistance.
When the load has zero resistance (R = 0), the current I will be limited only by the internal resistance r of the battery and will therefore have a maximum value. However, the p.d. across zero resistance is zero. No energy is transferred in the load but the battery will get very hot.
When the load resistance R is infinite, the current in the load will be very small. Again, the energy transferred in the load (IV) will be very small. It is reasonable that for some value of load resistance in between, the energy transferred will be a maximum. That value can be found using calculus, as in the following paragraph below:
Derivation of the maximum power theorem
In the circuit consisting of a battery of e.m.f ε, with internal resistance r connected to a load resistor R, we have:
ε = Ir + IR or I = ε/(r + R)
The power W in the load R is given by:
W = I2R = ε2R/(r + R)2
As R changes. So does W. W will be a maximum when dW/dR is zero:
dW/dR = d/dR[ε2R/(r + R)2] = 0
That is, the diferential =:
(r + R)2ε2 - 2ε2R(r + R) ÷ (r + R)4 = 0
Therefore:
(r + R)2ε2 - 2ε2R(r + R)
This simplifies to:
(r + R) – 2R = 0
Which gives the solution:
r = R
That is, the maximum energy transfer happens when the load resistance is the same as the internal resistance of the battery.
The same idea works in electronic systems except that we are dealing with alternating signals rather than d.c. Instead of resistance we consider impedance, but the result is the same: maximum power is transferred when the output impedance is equal to the load impedance.
PROPERTIES OF OPERATIONAL AMPLIFIERS
The operational amplifier or op-amp is nearly the perfect amplifier. Op-amps have some important properties:
- They are differential amplifiers. They have two inputs and the output of the amplifier depends on the difference between them:
output = gain × difference between the two inputs
One input is called the non-inverting input and the other is the inverting input.
Vout = A(ε1 - ε2)
For example, if A = 106, ε1 = 0 V and ε2 = 2 μV. Then:
Vout = 106(0 – 2) μV= -2V
Notice that when ε1 = 0, the output is negative – the amplifier is said to invert the input.
- They have a very high gain A, typically 105 to 106, with some having gains up to 109. This gain is called the open loop gain.
- All inputs and outputs are measured relative to earth (0 V). Most op-amps use a ‘split rail’ power supply which means that earth is taken as the mid-point of the power supply. The supply voltage limits the output voltage of the amplifier. Vout cannot be bigger than ±V.
- The inputs draw very tiny currents – so small that we can consider that they draw no current at all. That is. They have a very high input impedance. (A typical op-amp will draw a current much smalter than micro-amp, and often as low as nano amps.) A voltage of 1 pV at the input will drive a current of pA (1 pico-amp) into the op-amp.
- The output impedance is very low. This means that the output can deliver quite a high current, up to 20 mA.
OP-AMPS IN USE
Op-amps are not used by themselves. The simplest circuits use resistors – in particular, one between the input and the output. This provides feedback between the output and the input and makes some very useful circuits possible. In the examples described, the feedback is negative feedback. This means that a fraction of the output is ‘fed back’ to the inverting input.
The inverting amplifier
In an inverting amplifier, Rf is the value of the feedback resistor between the output and the inverting input. Rin is the input resistor value. The non-inverting input is earthed, that is, at 0 V.
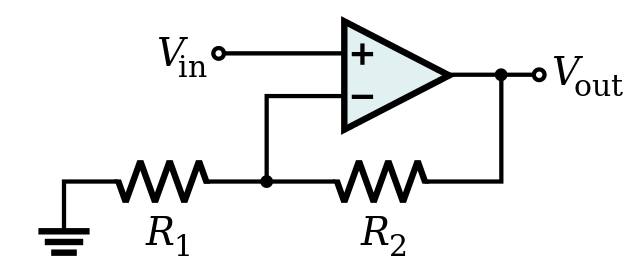
You will find it easier to understand this circuit if you try it out. If the values of the two resistors Rf and Rinare equal, the output voltage will be the same size as the input but it will also be inverted. That is, an input voltage of +1V will give an output of -1 V. To analyse how this circuit behaves, we must start at the output.
In analysing the behaviourof an inverting amplifier, the two resistors are effectively in series. The current drawn by the inverting put of the op-amp is very small compared with the current through the two resistors in series have the same current in them. So the mathematics of this circuit is fairly simple.
The output voltage can be a precise multiple or fraction of the input – it depends only on the two resistors. Notice that the output voltage doesn not swpwnd on any of the characteristics of the op-amp, yet the circuit would not work without it.
The circuit carries out a precise mathematical operation, in this case multiplication by a constant, the gain of this circuit (Vout/Vin). Which is called the the closed loop gain.
One way of looking at the circuit is to say that the output will become whatever value is necessary to make the difference between the two inputs equal zero. In this case, the output goes to a value that makes the inverting input zero. (The other input has been fixed at zero.) The voltage of the power supply limits the maximum output voltage from the amplifier. No matter what the theoretical gain of a circuit, it is impossible for the output to be bigger than the supply voltage. Real op-amps saturate at one or two volts short of the power supply voltage.
For example, if an op-amp is operating from a ±15V supply. Then the output will never be bigger than ±13 V, and so ±13 V is called the saturation voltage. This can be measured by plotting the transfer characteristic of the op-amp. The slope of the central part of the graph is the gain of the inverting amplifier Rf/Rin.
I guess I will be stopping here, till next time. Thanks for coming.
REFERENCES
https://www.electronics-tutorials.ws/amplifier/amp_1.html
https://www.instructables.com/id/Make-a-Simple-Audio-Amplifier/
https://www.animations.physics.unsw.edu.au/jw/dB.htm#:~:text=Definition%20and%20examples,intensity%20or%20several%20other%20things.
https://en.wikipedia.org/wiki/Maximum_power_transfer_theorem
https://www.tutorialspoint.com/network_theory/network_theory_maximum_power_transfer_theorem.htm#:~:text=Condition%20for%20Maximum%20Power%20Transfer&text=Therefore%2C%20the%20condition%20for%20maximum,will%20be%20of%20maximum%20value.
https://www.elprocus.com/operational-amplifiers/
https://www.allaboutcircuits.com/technical-articles/characteristics-of-operational-amplifiers/
https://en.wikipedia.org/wiki/Operational_amplifier
https://www.electronics-tutorials.ws/opamp/opamp_1.html
https://www.allaboutcircuits.com/textbook/semiconductors/chpt-8/introduction-operational-amplifiers/#:~:text=Op%2Damps%20are%20linear%20devices,ifferentiation).&text=The%20operational%20amplifier%20is%20arguably,device%20in%20analog%20electronic%20circuitry.
https://www.electronics-notes.com/articles/analogue_circuits/operational-amplifier-op-amp/inverting-amplifier.php
https://www.electronics-tutorials.ws/opamp/opamp_2.html
Congratulations @emperorhassy! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s) :
You can view your badges on your board And compare to others on the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPSupport the HiveBuzz project. Vote for our proposal!
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Thanks for using the STEMsocial app
and including @stemsocial as a beneficiary, which give you stronger support.
Thank you sir, it will helpful for Electrical Engineering Students