Hello, dear readers. I appreciate the @STEMSocial management for their support. And to all those that reached out to me, including some students of chemistry and researchers (on my discord and outside Hive) on how educative my posts are. Thanks, for all your beautiful comments.
Today, I will do as usual; by trying to explain all about gases as being taught in the classroom to a layman. I hope the post can serve as reference for students and other lovers of chemistry. I promise it’s gonna be interesting as usual. Let me introduce the chapter by explaining the chemistry of airbags.
INTRODUCTION: The chemistry of airbags
Airbags are a familiar addition to car safety these days. But a crash happens very fast, so how does the airbag inflate in time to protect the driver from injury? Airbags are usually inflated by a very fast gas-producing chemical reaction to blow up the bag.

First, the rapid deceleration of the car triggers an electric current, and the energy from this current explodes a detonator cap. The explosion makes the solid substance sodium azide (NaN3) decompose and release nitrogen gas extremely rapidly. The nitrogen inflates the airbag, cushioning the driver and reducing the likelihood of injury.
This is the equation for the decomposition of sodium azide:
2NaN3(s) → 2Na(s) + 3N2(g)
Sodium azide is a solid, so its particles are arranged very close together. The nitrogen it produces is a gas with widely spaced particles. For a relatively small amount of solid, the volume of gas that inflates the airbag is very large. At the same time, because the particles are now widely spaced, they can be compressed and so cushion the driver. The whole process takes about 40 milliseconds. Then, the specially designed bag deflates rapidly, so that the driver has vision and movement after the crash. This also applies where airbags are fitted for other passengers.
Airbags work, therefore, because of the different arrangements of particles in the different states of matter, an application of chemistry that regularly saves lives.
GASES
The Greeks thought that air was one of four elements that made up the Earth. Later, alchemists produced what they called ‘airs’ or ‘vapours’ in their efforts to change common metals, such as iron and lead, into gold. It was a Dutch scientist, Jan van Helmont, who realised that not all these ‘airs’ were the same, though they would fill any container they were put into.
The Greeks had a name for the substance that they thought the gods had changed into the four elements of Earth – chaos. In 1624, van Helmont used this word for ‘airs’. When pronounced in Dutch the word became ‘gas’. It is now recognised as a state of matter, together with the other two states solid and liquid.

VOLUMES OF GASES
Towards the end of the 18th century, chemists were experimenting with reactions that involved gases. The French chemist Joseph Gay-Lussac studied a large number of these reactions and realised that when gases reacted their volumes were in a simple whole number ratio, provided he measured the volumes at the same temperature and pressure. If the product was a gas this volume too was in a simple ratio to the reactants.
When Gay-Lussac reacted 5 dm3 of hydrogen gas with 5 dm3 of chlorine gas, he produced 10 dm3 of hydrogen chloride. The simple whole-number ratio for this reaction is:
1 volume of hydrogen : 1 volume of chlorine : 2 volumes of hydrogen chloride
1 volume of hydrogen + 1 volume of chlorine → 2 volumes of hydrogen chloride
5 dm3 + 5 dm3 → 10 dm3
Note: A decimetre is 10 cm. So a cubic decimetre (dm3) is 10 × 10 × 10 = 1000 cm3, which is the same as a litre.
In 1808, Gay-Lussac summed up his experimental observations in his law of combining volumes and said:
When gases react, they do so in volumes that bear a simple whole-number ratio to each other and to the volumes of any gaseous products, provided the temperature and pressure are the same when the volumes are measured.
AVOGADRO’S LAW
In 1811, an Italian named Amedeo Avogadro, a lawyer and later a professor of physics, put forward a theory to explain the experimental findings of Gay-Lussac and said:
Equal volumes of different gases contain equal numbers of molecules at the same temperature and pressure.
It took about 50 years of confusion before Avogadro’s theory was accepted. One of the stumbling blocks was John Dalton, who in 1803 had produced his atomic theory. He thought that all gaseous elements were made up of separate atoms. He did not understand, for instance, that hydrogen and chlorine were made up of H2 molecules and CI2 molecules. If Dalton had been right, and hydrogen and chlorine gas had been made up of atoms, then Avogadro’s theory would have suggested that these atoms were split.
Let’s try to follow Dalton’s argument to see if it is logical:
1 volume of hydrogen + 1 volumes of of chlorine → 2 volumes hydrogen chloride
Since, according to Avogadro’s theory, each volume must contain the same number of particles if they are measured at the same temperature and pressure, then:
1 million atoms of hydrogen + 1 million atoms of chlorine → 2 million molecules of hydrogen chloride
So: 1 atom H + 1 atom Cl → 2 molecules HCI
This is wrong. If it were correct, there would have to be two hydrogen atoms created from one. This confusion held up progress in chemistry for half a century.
However, if we accept that hydrogen and chlorine are made up of diatomic molecules, then the observations of Gay-Lussac are explained easily by Avogadro:
1 million molecules H2 + 1 million molecules Cl2 → 2 million molecules HCl
So: 1 molecule H2 + 1 molecule Cl2 → 2 molecules HCl
Avogadro’s theory is also called Avogadro’s law, because gases at low pressures obey it.
MOLAR GAS VOLUME
One mole is the amount of substance that contains as many particles as there are atoms in exactly 12 g of carbon-12. The number of particles in a mole is 6.02 × 1023 and is called the Avogadro constant, L. It is the unit chemists use for the amount of a substance. It follows from Avogadro’s law that the volume of one mole of any gas – the molar gas volume Vm must be the same under identical conditions of temperature and pressure, because we are dealing with the same number of particles.
At 273 K (0 °C) and a pressure of 101 kilopascals, kPa (1 atmosphere), 1 mole of gas occupies 22.4 dm3. These conditions of temperature and pressure are called standard temperature and pressure (s.t.p.). So, the molar gas volume at s.t.p. is 22.4 dm3. At 298 K and 101 kPa (sometimes called room temperature and pressure), the molar gas volume is 24 dm3.
So, here are some examples to really understand what I’m talking about.
Example 1.
What is the volume at s.t.p. of:
(a) 1 mol hydrogen, (b) 2 mol hydrogen chloride (c) 0.5 mol oxygen?
Remember: mol is the shortened form of the mole unit.
Answer
a) Since one mole of any gas occupies 22.4 dm3 at s.t.p., the volume occupied by hydrogen must be 22.4 dm3.
b) The amount of gas is 2 moles, so the volume of hydrogen chloride is double the molar volume at s.t.p., which is 44.8 dm3 (22.4 × 2).
c) Oxygen will occupy half the molar gas volume, since there is 0.5 mole present. 22.4 × 0.5 = 11.2 dm3.
CALCULATIONS FROM CHEMICAL EQUATIONS
An understanding of the laws of Gay-Lussac and Avogadro is very useful to chemists. It allows them to use equations to work out the volumes of gases required for a particular reaction, or to predict the volumes of gases that are produced by a given reaction.
Here are some other examples…..
Example 2:
A coal-fired power station uses fuel that contains 0.5 per cent sulphur by mass. What volume of sulfur dioxide at 298 K and 101 kPa is released into the atmosphere by burning 100 tonnes of coal?
Answer
Step 1: Write the balanced equation for the reaction:
S(s) + O2(g) → SO2(g)
(Remember that: (s) = solid, (l) = liquid, (g) = gas.)
Step 2: Convert the equation to amounts: 1 mol S gives 1 mol SO2
Note: In this example we do not need to know the number of moles of O2.
Step 3: Work out the amount being used (1 tonne is 1 000 000 g):
100 tonnes of coal contains 0.5 per cent S.
So the mass of S = 0.5 tonnes = 500 000 g.
Moles of S in 0.5 tonnes = mass (in grams) ÷ mass of one mole (in grams)
= 500 000 g/32 g
= 15 625 mol (ignoring sig. figs)
Step 4: Scale the amounts in the equation:
1 mol S produces 1 mol SO2
15 625 mol S produces 15 625 mol SO2
Step 5: Calculate the volume of gas:
1 mole of gas occupies 24 dm3 at 298 K and 101 kPa.
Volume of SO2 = 15 625 × 24 = 375 000 dm3
= 380 000 dm³ (to two sig. Figs)
Example 3
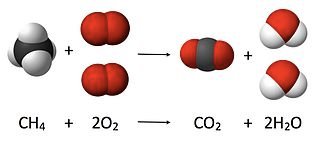
What volume of oxygen is required to burn 600 cm3 of natural gas under room conditions? Assume that natural gas is pure methane.
Answer
Step 1: Write the balanced equation for the reaction:
CH4(g) + 2O2(g) → CO2(g) + 2H2O(l)
Step 2: Convert the equation to volumes:
Since: 1 mol CH4 reacts with 2 mol O2
1 volume CH4 reacts with 2 volumes O2
Step 3: Use the simple whole number ratio of volumes to work out the actual volume used:
600 cm3 CH4 reacts with 2 × 600 cm3 O2
So the volume of oxygen used is 1200 cm3.
So as not to make the post too bulky, I will stop here and continue in my next post; where I will discuss the gas laws and the kinetic molecular model for how gases behave.
Thanks for reading.
REFERENCES
https://www.scientificamerican.com/article/how-do-air-bags-work/
http://www.chemistry.wustl.edu/~edudev/LabTutorials/CourseTutorials/bb/Airbags/151_T5_07_airbags.pdf
https://www.livescience.com/53304-gases.html
https://en.wikipedia.org/wiki/Gas
https://en.wikipedia.org/wiki/Jan_Baptist_van_Helmont
http://www.shodor.org/unchem/advanced/gas/
https://byjus.com/chemistry/gay-lussacs-law/
https://en.wikipedia.org/wiki/Gay-Lussac%27s_law
https://www.britannica.com/biography/Joseph-Louis-Gay-Lussac
https://en.wikipedia.org/wiki/Avogadro%27s_law
https://www.britannica.com/science/Avogadros-law
https://en.wikipedia.org/wiki/John_Dalton
https://www.britannica.com/biography/John-Dalton/Atomic-theory
https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules
https://www.bbc.co.uk/bitesize/guides/zwbyjty/revision/4
https://en.wikipedia.org/wiki/Molar_volume
https://socratic.org/chemistry/the-behavior-of-gases/molar-volume-of-a-gas-224-l-at-stp
http://nobel.scas.bcit.ca/wiki/index.php/Calculations_based_on_chemical_equations
https://www.bbc.co.uk/bitesize/guides/zds48mn/revision/1
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @steemstem account (for some ROI).
Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support.