Hello, dear readers, my beloved students and erudite colleagues. Today on All About Gases as being taught in the classroom, I would start by explaining how gases behave according to the kinetic molecular theory.
A KINETIC-MOLECULAR MODEL FOR HOW GASES BEHAVE
So far, I have considered experimental observations of the behaviour of gases that relate pressure, volume, temperature and amount through the ideal gas equation. The concise statements of these observations we have called laws, because they are true for all gases under a range of conditions.
However, scientists soon began to produce models to explain gas behaviour. The simple model that we accept today for the behaviour of ideal gases is called the kinetic-molecular model or the kinetic theory, after the Greek work kinein, to move. Several notable scientists developed the model in the nineteenth century, in particular Ludwig Boltzmann, an Austrian, and James Maxwell, a Scot.
In the kinetic-molecular model, ideal gases are assumed to be made up of particles (atoms, molecules or ions) that:
- are very widely separated;
- have negligible (zero) volume;
- exert no force of attraction on each other;
- move continuously and randomly;
- have perfectly elastic collisions with each other and the container walls (this means that there is no net gain or loss of energy in collisions);
- have an average kinetic energy that is directly proportional to the absolute temperature of the sample.
Remember that kinetic energy is the energy due to the motion of the particles. Not all molecules move at the same speed, or velocity, at any particular temperature above 0 K, so molecules possess a range of kinetic energies at a particular temperature. For example, in any sample of gas, some molecules will be moving very fast, while others will be moving fairly slowly. This range of speeds leads to a range of energies. I will talk more on this when I’m discussing the Maxwell-Boltzmann distribution of molecular energies.
Now that we have a model we can see how well it fits the experimental observations – the true test of any model.
Gases can be compressed – the kinetic-molecular model explains this because the particles are widely spaced. Boyle’s law – the collisions of particles with the container walls cause pressure. Two factors determine the pressure: the number of collisions in a certain time on a specific area, and the force of these collisions. If we keep the temperature and amount of gas particles constant and decrease the volume of the container that the gas is in, more particles will collide with a specific areas of container wall, so the pressure will increase. Boyle’s law explained by the kinetic theory: When there is a fixed amount of gas at constant temperature and the pressure is doubled, the volume will be decreased by half.
Charles’ law – according to the kinetic-molecular model, the average kinetic energy of the particles is proportional to the absolute temperature. As the temperature of a gas increases, so does the average kinetic energy of its particles. This means that the particles will collide with the container walls more often and with greater force. So doubling the absolute temperature doubles the average kinetic energy of particles in a gas, which leads to a doubling of volume provided the pressure stays constant. Charles’ law explained by the kinetic theory: If the amount of gas and pressure remain the same but as the temperature doubles the average kinetic energy of the molecules also doubles to cause a doubling of the volume.
REAL GASES
So far, we have looked at ideal gases that obey the ideal gas equation exactly under any conditions. In the calculations, we have assumed that gases behave ideally, and at room conditions this assumption is a good one. However, the kinetic-molecular model assumes that particles in a gas have negligible (zero) volume. This is reasonable at room temperature and pressure, when the particles are very widely spaced. But as the particles in a gas squeeze closer together, their volume becomes significant. The kinetic-molecular model also assumes that there are no attractive forces between molecules. This, again, is reasonable provided that the particles are far apart, but, as they draw closer together, forces of attraction are increasingly important. The higher the temperature, the faster the particles move, which also tends to make the forces of attraction between particles negligible. Thus the conditions that allow a gas to approach ideal gas behaviour are high temperatures and low pressures.
Conditions in which real gases do not show ideal behaviour are those that bring the particles close together. At low pressures the particles are far apart, so their volume is negligible compared with the volume of the gas. At high pressures the gas particles take up a larger proportion of the volume, so the volume of the particles becomes significant. Also, because the particles are closer together, attractive forces can operate.
Again, at low temperatures the speed of the particles is slower, so forces of attraction between them can operate. At the boiling point of a substance the forces of attraction are great enough to allow the gas to condense to a liquid. So the closer the temperature of a gas is to its boiling point, the more it will deviate from ideal behaviour. This can be seen for nitrogen gas. If nitrogen were an ideal gas it would obey the ideal gas equation, pV = nRT. So if we had one mole of nitrogen: pV/RT = 1.
A graph of pV/RT can be plotted against pressure, and at any pressure the value should be 1. However, at a low temperature of 203 K the graph shows wide deviation from this value, while at higher temperatures the deviation from ideal behaviour is much less.
HOW PARTICLES ARE ARRANGED IN LIQUIDS AND SOLIDS
The kinetic-molecular model can be extended to include the liquid and solid states of matter. The particles in a liquid are much closer together than they are in a gas, and because of this they exert considerable attractive forces on each other. The particles are also free to move, but are much slower than in the gas.
In the solid state, particles are even closer than liquids, so while it is possible to compress liquids slightly, solids are almost incompressible. The particles are also fixed into position, held by attractive forces, vibrating but not free to move out of position. This three-dimensional arrangement of particles gives solids a definite shape and is called a lattice. Most solids are crystalline, which means that the particles are arranged in an orderly way.
However, not all solids are crystalline. Glass may have a fixed shape and so we call it a solid, but the arrangement of its particles has the disorder associated with a liquid.
THE KINETIC-MOLECULAR MODEL USED TO EXPLAIN CHANGES IN STATE
It takes energy to change a substance from a solid to a liquid and then to a gas. As energy is transferred to a solid, the particles vibrate more until they break out of their fixed lattice positions. This is when the solid melts. There is no change in temperature during this time, because all the energy transferred to the substance goes into overcoming the forces that hold the particles in the lattice. The energy needed to change one mole of substance from a solid to a liquid at the melting point is called the enthalpy change of fusion (ΔHm). When all the solid has melted, the temperature begins to rise and the particles have more energy and move faster.
At the boiling point, the liquid begins to change into a gas and the temperature again stays constant, since all the energy taken in by the liquid is used to overcome the forces that hold the particles close together in the liquid state. The enthalpy change of vaporisation (ΔHm) is the energy that must be supplied to change one mole of liquid into a gas at a particular temperature. When all the liquid has boiled to form a gas, the temperature rises again as the particles move faster. The process of changing state is a physical process because no chemical bonds are broken.
Liquid crystals: Another State of Matter
You often come across liquid crystal displays (LCDs): the numbers displayed on a digital watch use liquid crystals, you may have seen liquid crystal thermometers that change colour depending on the temperature, and laptop computer screens also use liquid crystals. LCDs are commonplace now, but they have only been around for about 50 years.
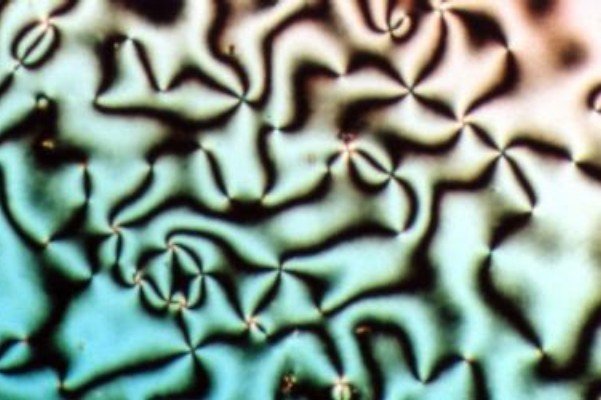
When crystals melt, the ordered crystalline arrangement of their particles breaks down into the disordered liquid state. However, some crystals melt to give particles in an ordered state. This effect was first noticed over 100 years ago by an Austrian botanist, Friedrich Reinitzer. He was heating cholesteryl benzoate to try to determine its molecular structure, and noticed that at 146°C a cloudy liquid was produced. The liquid went completely clear at 178°C. This process was reversible on cooling. Reinitzer had discovered a new state of matter that was intermediate between the liquid and solid states.
The liquid crystal state was an interesting curiosity, but thought to be of no practical use since there were no stable compounds that showed the liquid crystal state at room temperature. In the late 1960s, the search was on to replace the heavy cathode-ray tubes in aircraft. (Older televisions use a cathode-ray tube.) There was renewed interest in trying to produce chemicals that showed liquid crystal properties at room temperature. In 1972 at Hull University, the world’s first stable, room-temperature liquid crystal was made.

Liquid crystals nearly always contain thin, rigid organic molecules. There are three different arrangements of molecules in the liquid crystal state. The one that is used in digital watches and computer display screens is called nematic. In a digital watch or calculator display, a mirror at the back of the display reflects light from the surroundings. An electric field alters the orientation of the liquid crystal molecules in a thin film; this causes the display to go dark. The computer display of a laptop is lit from the back of the display by fluorescent tubes and the liquid crystals are arranged in pixels (small parts of the image) with red, green or blue filters above them to give a coloured image. By altering the electric field in each pixel the orientation of the liquid crystal molecules is changed and a coloured image is generated.
Another arrangement of liquid crystals gives different colours at different temperatures and these are used in thermometers. Liquid crystals are now very big business and a lot of research is under way to produce new molecules that show this interesting state of matter.
I will pause here for now. I will discuss about the vapour pressure and the unusual behaviour of water.
Thanks for coming.
REFERENCES
https://opentextbc.ca/introductorychemistry/chapter/kinetic-molecular-theory-of-gases-2/
https://courses.lumenlearning.com/introchem/chapter/kinetic-molecular-theory-and-gas-laws/
https://en.wikipedia.org/wiki/Real_gas
https://opentextbc.ca/introductorychemistry/chapter/real-gases-2/
https://www.researchgate.net/post/What_are_real_gases_What_are_their_applications
https://www.bbc.co.uk/bitesize/guides/z2wmxnb/revision/4
https://www.siyavula.com/read/science/grade-8/particle-model-of-matter/06-particle-model-of-matter?id=toc-id-4
https://www.chem.purdue.edu/gchelp/liquids/character.html
https://study.com/academy/lesson/the-kinetic-molecular-theory-properties-of-solids-and-liquids.html
https://www.siyavula.com/read/science/grade-10/states-of-matter-and-the-kinetic-molecular-theory/03-states-of-matter-and-the-kinetic-molecular-theory-02
https://courses.lumenlearning.com/boundless-chemistry/chapter/kinetic-molecular-theory-of-matter/
https://www.le.ac.uk/se/centres/sci/selfstudy/particle02.html
https://www.sciencedirect.com/topics/materials-science/liquid-crystal
https://www.britannica.com/science/liquid-crystal
https://en.wikipedia.org/wiki/Liquid_crystal
@tipu curate
Upvoted 👌 (Mana: 0/2)
Congratulations @empressteemah! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s) :
You can view your badges on your board and compare to others on the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @hivebuzz:
Support the HiveBuzz project. Vote for our proposal!
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @steemstem account (for some ROI).
Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support.