¡Hola querida comunidad científica de #Hive, reciban todos un cordial saludo!🖐
Hello dear #Hive scientific community, receive warm greetings from all of you!🖐
Hace algún tiempo para esta comunidad estuvimos desarrollando un tema muy importante en matemática y las ciencias naturales, se trata de magnitudes vectoriales. En dicha publicación hablamos de la definición y ejemplos de vectores, así como también de sus características que son el módulo, la dirección y el sentido además de aprender a calcular su magnitud.
Some time ago for this community we were developing a very important topic in mathematics and natural sciences, it is about vector magnitudes. In this publication we talked about the definition and examples of vectors, as well as their characteristics which are the module, the direction and the sense in addition to learning how to calculate their magnitude.
Imagen realizada con la página web de diseño gráfico y composición de imágenes Canva // Image made with the graphic design and image composition website Canva.
En esta ocasión, veremos lo que son las componentes rectangulares. Antes que todo es propicio preguntarnos, ¿Qué son las componentes rectangulares de un Vector? Las mismas las podemos definir como dos vectores perpendiculares, que al momento de sumarlos dan como resultado el vector inicial, también se puede decir que son las protecciones del vector hacía los ejes del plano de coordenadas. Veamos el vector que se presenta a continuación:
This time, we will see what the rectangular components are. First of all it is appropriate to ask ourselves, what are the rectangular components of a Vector? We can define them as two perpendicular vectors, which when added together result in the initial vector, we can also say that they are the protections of the vector to the axes of the coordinate plane. Let's see the vector presented below:
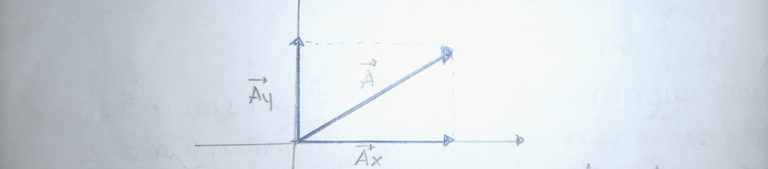
Si analizamos un poco la definición de componentes rectangulares, la cual resalta que son las proyecciones hacía los ejes, también se puede decir que son las sombras que hace el vector en los ejes horizontales y verticales; dichas sombras también son vectores.
Es importante saber, que cuando que cuando la componente “x” va hacia la derecha entonces la componente es positiva; pero si va hacia la izquierda, entonces la componente es negativa. Lo mismo ocurre con el eje “y” cuando va hacia arriba es positiva; y cuando la componente va hacia abajo es negativa.
Otro aspecto muy interesante a considerar, es que no necesariamente el vector debe iniciar en el origen. Si por ejemplo, se toma el vector A y se mueve de posición, este suceso no altera las componentes del vector. Analicemos el siguiente vector:
If we analyze a little the definition of rectangular components, which highlights that they are the projections to the axes, we can also say that they are the shadows that the vector makes on the horizontal and vertical axes; these shadows are also vectors.
It is important to know that when the "x" component goes to the right then the component is positive; but if it goes to the left, then the component is negative. The same happens with the "y" axis when it goes upwards it is positive; and when the component goes downwards it is negative.
Another very interesting aspect to consider is that the vector does not necessarily have to start at the origin. If, for example, vector A is taken and moves position, this event does not alter the components of the vector. Let's analyze the following vector:
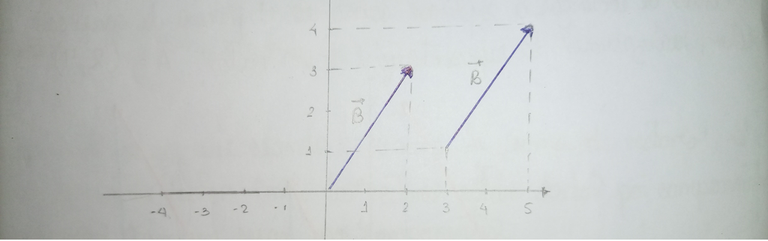
En la gráfica anterior, dibujamos el mismo vector, la diferencia es que uno sale desde el origen y el otro no. Sin embargo, cuando revisamos las componentes son exactamente iguales, dos espacios en “x” y tres espacios en “y”. Si se mueve el vector hacía los negativos seguirá midiendo lo mismo y la componente en “x” será positiva porque va hacia la derecha y la componente “y” igual porque va hacia arriba.
Ahora bien, hay un caso particular y es que cuando los vectores son verticales y horizontales, las componentes cambian. Cuando el vector es vertical sólo tendrá componente “y” y cuando es horizontal sólo tendrá componente “x”. Observemos con detenimiento las siguientes gráficas:
In the previous graph, we draw the same vector, the difference is that one leaves from the origin and the other does not. However, when we check the components they are exactly the same, two spaces in "x" and three spaces in "y". If you move the vector to the negatives it will still measure the same and the component in "x" will be positive because it goes to the right and the "y" component the same because it goes up.
Now, there is a particular case and it is that when the vectors are vertical and horizontal, the components change. When the vector is vertical it will only have a "y" component and when it is horizontal it will only have an "x" component. Let's take a closer look at the following graphs:
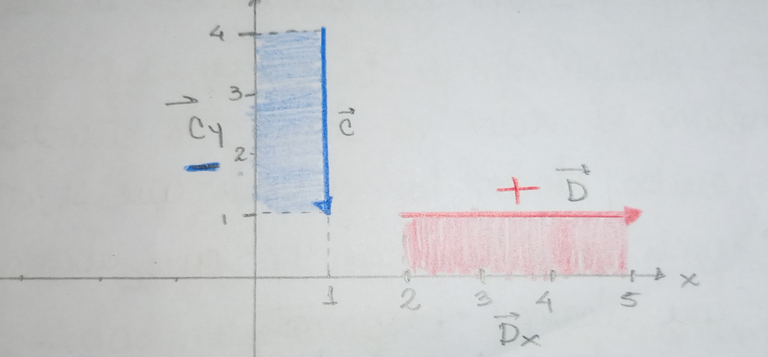
El vector C sólo tiene sombra en el eje “y” y su componente es negativa porque el vector va hacia abajo. Mientras que el vector D sólo tiene sombra en el eje “x”, pero la componente es positiva porque va hacia la derecha.
Vector C only has shadow on the y-axis and its component is negative because the vector goes downward. While vector D only has shadow on the "x" axis, but the component is positive because it goes to the right.
Representación gráfica de un vector por componentes // Graphical representation of a vector by components
Antes de comenzar a explicar cómo es el proceso de graficar un vector, realizaremos la representación de un vector A = (2,4).
Before we begin to explain how the process of graphing a vector works, we will represent a vector A = (2,4)
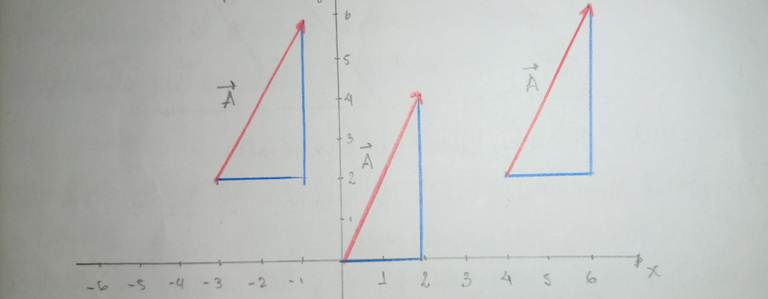
Cuando se nos presentan las coordenadas “x” y “y” para graficar un vector siempre tendemos a graficar desde el origen, y eso es correcto. Sin embargo, un vector puede iniciar desde donde deseamos, siempre y cuando cumpla con las componentes presentes, todas las representaciones vectoriales que están expuestas pertenecen a las coordenadas (2,4).
Resulta que la información que suministra dicha coordenada A = (2,4) obviamente nos dice que una es para “x” y otra para “y”. Pero también nos dice que 2 al ser positivo el vector va hacia la derecha y 4 por ser positivo va hacia arriba; si analizamos bien las gráficas antes presentadas vemos que todos los vectores dibujados cumplen con eso, una componente en “x” que abarca dos espacios, y una componente en “y” que abarca cuatro espacios. De esta manera es como se representan gráficamente las componentes de un vector.
When we are presented with the "x" and "y" coordinates to plot a vector we always tend to plot from the origin, and that is correct. However, a vector can start from wherever we want, as long as it complies with the components present, all vector representations that are exposed belong to the coordinates (2,4).
It turns out that the information supplied by that coordinate A = (2,4) obviously tells us that one is for "x" and one is for "y". But it also tells us that 2 being positive the vector goes to the right and 4 being positive it goes upwards; if we analyze well the graphs before presented we see that all the drawn vectors comply with that, a component in "x" that covers two spaces, and a component in "y" that covers four spaces. This is how the components of a vector are represented graphically.

Ya para despedirme, agradezco a quienes se tomarnos unos minutos de su tiempo para leer mi publicación y me encantaría poder leer en los comentarios sus opiniones e impresiones sobre el tema.
In closing, I would like to thank those of you who took a few minutes of your time to read my publication and I would love to read in the comments your opinions and impressions on the subject.

Referencias
Baldor, A. (1941). Algebra. México, Publicaciones Cultural.
Hinds, J. (2002). Matemática 8. Caracas, Editorial Premier.
References
Baldor, A. (1941). Algebra. Mexico, Cultural Publications.
Hinds, J. (2002). Matemática 8. Caracas, Editorial Premier.

Translator Deepl



Posted Using InLeo Alpha
From Venezuela, our witness drives decentralization and the adoption of Web3 technology, creating opportunities for the local community and contributing to the global ecosystem. // Desde Venezuela, nuestro testigo impulsa la descentralización y la adopción de la tecnología Web3, generando oportunidades para la comunidad local y contribuyendo al ecosistema global.
Sigue, contacta y se parte del testigo en: // Follow, contact and be part of the witness in:
Gracias @hispapro por el apoyo
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.
Gracias @stemsocial
~~~ embed:1801045202003444123?t=mlTZgoURxgact-7_8kEuJw&s=19 twitter metadata:SUxvdmVQaHlzaWNhfHxodHRwczovL3R3aXR0ZXIuY29tL0lMb3ZlUGh5c2ljYS9zdGF0dXMvMTgwMTA0NTIwMjAwMzQ0NDEyM3w= ~~~