Happy Monday and welcome to my particle physics weekly blog.
This post may be my last contribution to STEMsocial and HIVE for 2021, as school vacation starts on the 18th in France. Even if it is less and less clear that I will go anywhere (thanks COVID for this), organising activities with the boys will indeed naturally send the computer to its storage bag and reduce screen time. However, I may be able to do something in the evenings/nights (I sleep efficiently), and thus find some time to write a text next week.
In my last blog, I detailed how the hard work of physicists during the last hundred years led to what is called the Standard Model of particle physics. By trying to understand how matter functions and is organised at its most fundamental level, they ended up with a theoretical framework based on six types of quarks (up, down, charm, strange, bottom and top), three charged leptons (electron, muon and tau) and three neutrinos (electron, muon and tau neutrino). These twelve elementary particles form the basic building blocks of matter.
Matter is of course not inert and interacts. The Standard Model includes three classes of interactions, namely electromagnetism, weak interactions and strong interactions. In the theory those interactions are modelled through so-called gauge symmetries, which I deliberately didn’t describe deeply. What needs to be known, for the purpose of this blog, is that particles interact when they exchange force carriers. We have one or more of such force carriers for each of the three fundamental interactions, i.e. the photon (electromagnetism), the W and Z bosons (weak interactions) and the gluons (the strong force).
The most impressive success of the Standard Model is that once a handful of parameters are fixed, it yields predictions that agree with (almost) all data accumulated over the last hundred years. However, there is a catch. The gauge symmetries are symmetries, which means that anything that is not symmetric in the theory should be forbidden. One consequence of this is that all matter should be massless. Of course, matter is massive, as strongly testified by experiments.
[Credits: CERN]
This is the starting point of the present blog, that will address the Higgs boson and the Brout-Englert-Higgs mechanism. As can be guessed, both are connected to the 2013 Nobel prize in physics. In comparison to the blog of last week, the present post will bring us into a shorter journey of about 60 years of Higgs hunting. I however insist on the fact that this hunt is not over, and we probably still need at least another 75-100 years to finalise it.
The success of the Standard Model
As mentioned in the introduction to this blog, gauge symmetries work incredibly well.
In practice, the theory comes with a bunch of free parameters (a couple of dozens in our case), that are fit from data. Once this fit is done, we can readily use the theory (and the gauge symmetries it relies on) to make any predictions relevant for past, present or future experiments. In the previous blog, I have shown one of the dinosaur plots provided by the ATLAS experimental collaboration to illustrate this point. Note that this funny name is sometimes also heard in the high-energy community, and reflects how the results are organised in the figure. By paying some attention, we can indeed see a brontosaurus emerging from the figure…
Another great example comes from the so-called electroweak fit presented below. Before moving on with the Higgs boson (that is the topic of this blog), I will spend a few words to explain what is precisely the very important figure below.
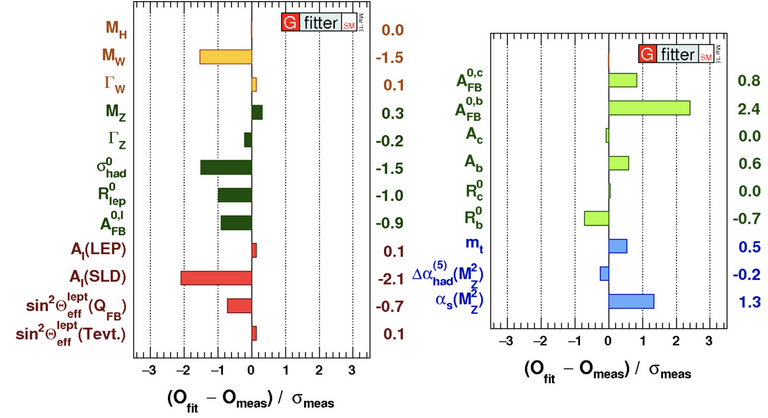
[Credits: GFitter]
First, a fit of the Standard Model parameters has been done from the data we have, using a usual minimisation of the test statistics 𝜒2 (this reads chi squared). This fit relies on various experimental measurements. It uses on the one hand the associated Standard Model theoretical predictions, and on the other hand the corresponding experimental inputs. In order words, we use data to extract as best as we can the values of all Standard Model free parameters.
From there, we next compare the fit results and the measurements, and estimate the deviations between the two. Those deviations are what is shown on the figure: a large coloured bar means a large deviation, while a small coloured bar means a good agreement. But what do large and small mean in this context? We indeed see both very small bars and some larger ones.
The deviations are shown in terms of standard deviations, or 𝝈 (this is the Greek letter sigma). The amount of 𝝈 tells us how much is a deviation significant.
A good example to explain what are these sigmas consists of a coin that we toss 100 times. We expect to get 50 results with the tail up, and 50 results with the head up (if the coin is unbiased). If you do the test at home, you may actually get 50 tails, but also 45, 51 or even 59 tails. In fact, many results are possible (but some are less probable).
Let’s now get wild and redo this 100-toss test 1000 times. For each of those 1000 experiments, we report the number of tails. Please do it at home, but only if you want and if you have nothing else to do (as this may be rather time-consuming). What we will see that most of the results will be 50. However, we will also have a bunch of 49 and 51, a smaller number of 48 and 52, an even smaller number of 47 and 53, and so on.
Let’s now report this on a graph. A standard deviation of 1𝝈 defines a symmetric region around 50 in which about 68% of all the 1000 results are included. A standard deviation of 2𝝈 includes about 95% of all results, and of 3𝝈 includes 99.7% of all results. These 1𝝈, 2𝝈 and 3𝝈 are what we see on the x-axis of the figure above. This thus evaluates how a particular data point (a measurement) could be inconsistent with the model (the Standard Model).
On the figure, we see that every single measurement features less than 3 standard deviations, most of them being in fact even below the 1𝝈 level. This is again what we called before an excellent agreement of the Standard Model with data. In high-energy physics, a hint for a new phenomenon corresponds to a 3-sigma significance. In contrast, a discovery requires 5 sigmas. To go back to the percentages above, we are talking here of about 99.99994%. We should better be sure before claiming about something new, and verify that the observation is not cursed by any unexpected random error!
The origins of the Higgs boson
I have so far shown another important example illustrating the great success of the Standard Model and the gauge symmetries it relies on. However, if those symmetries are realised, then all elementary particles should have zero mass. This strongly contradicts experiment! We are thus left with a big puzzle: a theory that works amazingly well, but that includes a big failure (among others which I won’t cover in this blog).
There is however a cure, that keeps the context of gauge symmetries alive and restores the particle masses. This is what is known as the Brout-Englert-Higgs mechanism. Using an idea from Anderson that dated from 1962, Brout and Englert (see here), and then Higgs (see here), applied it to the Standard Model in 1964.
In order to explain clearly what this idea is, we can use the image of a ball inside a bowl (that comes from the 2013 Nobel prize press release).
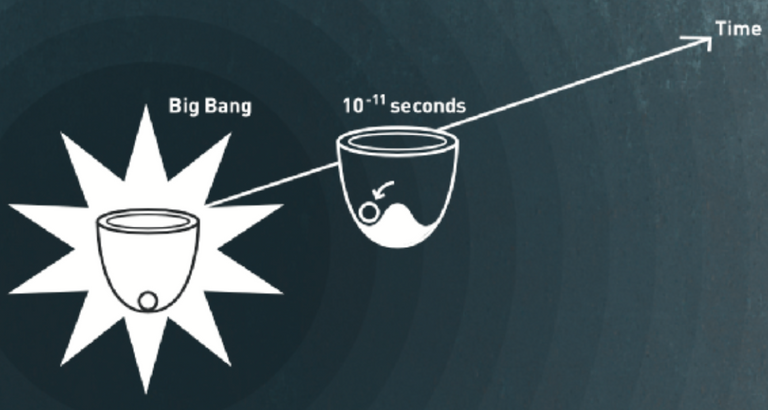
[Credits: Nobel Prize]
At the very beginning, the universe is symmetric. The gauge symmetries are realised and all particles are massless. We focus on the left of the above picture. If we push the ball that lies in the centre of the bowl a little bit up, it falls back at the centre. The symmetry is there, and stays there!
However, very quickly in the Universe history (at 10-11 second after the Big Bang) something happens and hides the symmetry from us. There is now a bump at the bottom of the bowl. Such as bump makes the ball rolling down in any direction. Afterwards, if we push a little bit the ball up, it does not go back to the centre anymore and stays instead down.
The centre is a position in which the symmetry is visible. We see from it the rotational symmetry around the vertical axis. However, when the ball lies in a position away from the centre, the symmetry is hidden. We indeed don’t see it from down there.
This is what the Brout-Englert-Higgs mechanism does. We say that the gauge symmetries are spontaneously broken. In fact, the fall of the ball from the central position is nothing but a phase transition (like water turning into ice).
Now the hot question is the following: what are the visible effects of this phase transition?
The answer is quite concise: there must exist one new particle, the Higgs boson. Before 2012, this particle needed to be found. But that’s not all. Finding a Higgs boson was one thing. However, finding a Higgs boson with properties as expected from the Standard Model was another thing. The former has been achieved on July 4th 2012, but the second one is still an open quest today.
I will now give more details on these two points (finding the Higgs boson and making sure it the discovered particle has the right properties).
Hunting for the Higgs boson
As said before, we are thus left with two tasks: finding the Higgs boson and verifying that it has the right properties (namely those expected from the Standard Model). The only problem is that we had no idea where to look at, at least in the early 1990s.
For the following, I recall that according to special relativity mass is equivalent to energy. This means that searching for a light Higgs boson would require experiments running at lower energies than in heavier cases. However, the Higgs boson could have (almost) any mass. This is precisely the source of the problem: if we want to produce a Higgs boson at accelerators, we have no idea of the collision energy that would be needed to produce it.
This being said, there is a theoretical upper bound on the mass of the Higgs boson. There is hence a maximum value so that the Higgs boson cannot be too heavy. However, anything below this upper value is possible, which leaves a very large number of possibilities.
To fix the ideas, let’s discuss numbers in terms of the proton mass (which is the mass of the nucleus of a hydrogen atom). The above-mentioned theoretical upper bound is equal to about 1000 times the proton mass. For comparison, the value for the Higgs mass as measured at the Large Hadron Collider is equal to 125 times the proton mass (which is a bit larger than the mass of a silver atom).
So, now we can ask ourselves about how this value of 125 GeV (GeV is the energy unit in particle physics, the proton mass being equal to 1 GeV) has been found among so many options?
To answer this question, the story starts in the 1990s with the Large Electron Positron (LEP) collider at CERN. This collider is the one that was preceding the Large Hadron Collider. Here, one beam of electrons and one beam of positrons (the antiparticle of the electron) were accelerated to high energies. Different collision energies were reached during the course of the experiments, the largest ones being of about 200 GeV, or 200 times the proton mass.

[Credits: CERN]
Many light options for the Higgs bosons were probed at this accelerator. Unfortunately, no ‘signal’ has been observed. For now, let’s consider a Higgs boson signal as being the difference between predictions for a given process with a Higgs boson, and the same predictions but without the Higgs boson (more detailed information will be given below).
As a result of these non-observations, the hypothesis of a Higgs boson mass lying below 114 GeV was excluded. In other words, around year 2000 the Higgs boson mass could be anything between 114 GeV and 1000 GeV.
Another collider, the Tevatron at Fermilab in the US, was also searching for the Higgs boson at the end of the 20th century and the beginning of this millenium. The Tevatron operated from the 1980s to the end of 2011. This machine was different from LEP in the sense that instead of smashing electrons and positrons, it was smashing accelerated protons and antiprotons.
Whereas much higher energies were available (roughly 2000 GeV), no Higgs boson was unfortunately found in data. As a consequence, constraints on the possible masses were again set: Higgs boson masses between 160 and 170 GeV were excluded. Again, this left many options possible, and the quest was still unresolved…
At the end of the life of the Tevatron, the Large Hadron Collider (LHC) at CERN had started to operate at a higher energy than the Tevatron one. Two beams of protons were here accelerated at 99.99999% the speed of light, leading to a collision energy of 7000-8000 GeV. However, despite of such a large energy being available, again no Higgs boson was found until the end of 2011.
The situation in 2011 is summarised in the plot below (it is homemade!). The x-axis represents all mass options allowed theoretically, and anything that is coloured is excluded by one or the other of the colliders above-mentioned.
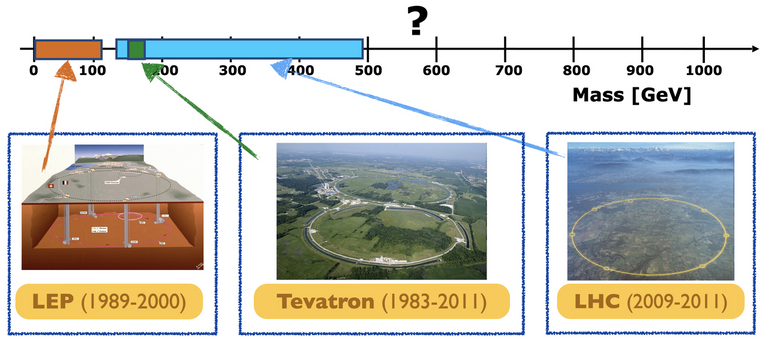
[Credits: @lemouth]
We can see that all lighter mass options were excluded, with the exception of a few values around 125 GeV. This is actually the location where the Higgs boson was waiting for us.
4th July 2012 and beyond: from the discovery to today
A milestone in the Higgs boson story is definitely July 4th, 2012. On that day, the ATLAS and CMS collaborations announced that after all these years, the long awaited Higgs boson had been discovered!
In order to understand how the discovery happened, it is good to focus now on what is a ’Higgs boson signal’. First, let me recall that the Higgs boson is related to the particle masses. Its couplings to the different particles of the Standard Model are therefore stronger for heavy particles (like the top quark or the electroweak Z or W bosons) than for lighter ones (like electrons or light quarks). In this way, if produced, the Higgs boson will preferably decay into heavier particles than lighter ones.
This consideration allows us to define the most frequent signatures to study in order to look for a Higgs boson, or in order words the best signs to look for in the LHC detectors that would correspond to the production and decay of a Higgs boson. The selection of the signatures to consider also accounts for the background of the Standard Model, where the background corresponds to all Standard Model processes leading to the same final state but without any Higgs boson.
The idea is to use a signature for which the signal is frequent enough, but that also yields a not too important background, or at least a reducible one. An example is shown in the image below, in which we can see predictions for a given measurable quantity. The background comprises several Standard Model processes and corresponds to the sum of the light blue, dark blue and green contributions.
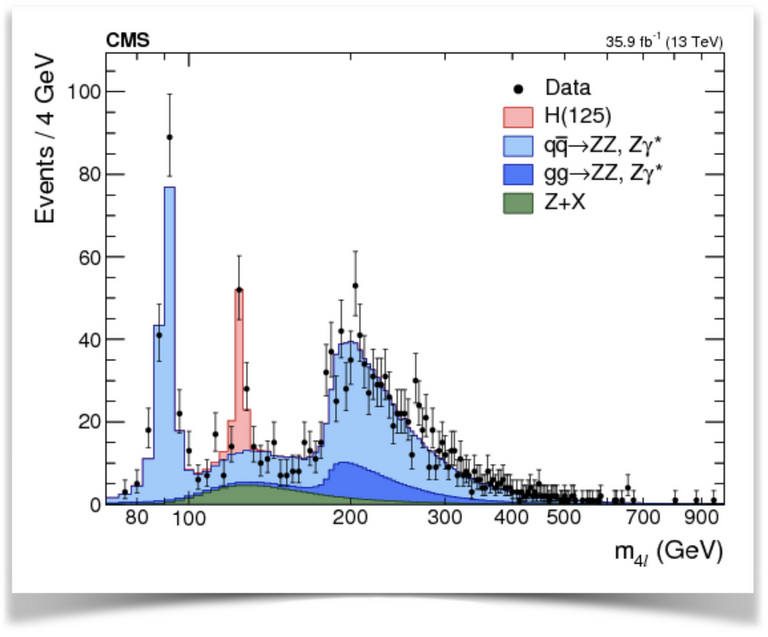
[Credits: CMS collaboration]
The data points (in black, with their error bars) require the red contribution, that consists of the Higgs boson signal. Without a Higgs boson (i.e. without the red contribution), data and theory would disagree very strongly. With the Higgs boson, everything is on the contrary very fine.
This plot is the 2017 version of the discovery plot of 2012, the latter containing less data. It was however significant enough so that we could conclude that the Higgs boson had been discovered, which then led to the Nobel Prize in physics in 2013.
While I have shown only one figure, several signatures have been investigated. In each case, Higgs boson contributions were needed to explain data. In other words, a particle with a mass of 125 GeV had been discovered. We can note that on the x-axis in the figure above, the red peak lies right at 125 GeV!
At this stage, what we know is that we have a Higgs boson, but not necessarily the Higgs boson. To conclude about this, we need to measure precisely the properties of the new boson. In particular, we need to make sure that all couplings of the Higgs boson are proportional to the particle masses. This has of course been done, and the results (see the image below) show a great agreement.
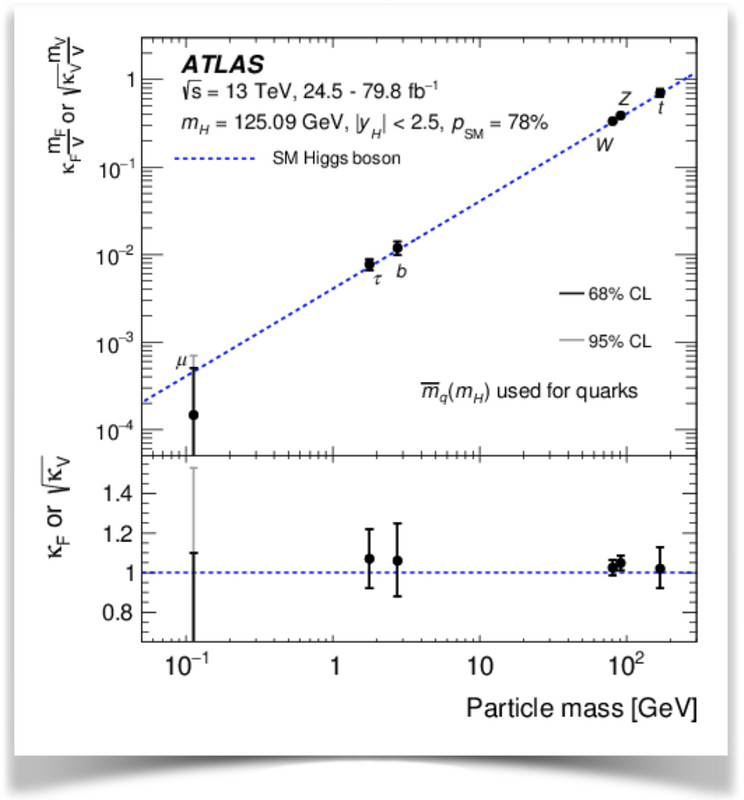
[Credits: ATLAS collaboration]
However, only a few couplings have been tested so far. We indeed can see data points only for the heavier particles: the top quark, the W and Z bosons, the bottom quark, the tau lepton and the muon (although with a very large error bar). This is the reason why we can say that the quest for the Higgs boson is actually still on-going.
In order to be able to conclude that the Standard Model is the true theory of nature without any doubt (and we have doubts), we need to measure every single coupling of the Higgs boson, including its self-couplings that are very challenging both for the Large Hadron Collider and at any of its proposed successors.
50 more years of Higgs hunting
It is now time to finish this blog, which took me quite a long time to write (but this was fun). I have tried to explain how physicists came up with the idea of the Higgs boson. On the one hand, we had the Standard Model of particle physics, a theoretical framework that is working incredibly well. On the other hand, the Standard Model without the Higgs is associated with a variety of issues, the most stressing one (but not the only one) being the fact that elementary particles need to have zero mass.
The discovery of the Higgs boson in 2012 was a great milestone in our understanding of nature, as it validated the Standard Model somehow. It is however not the last step, as we are now left with the task of verifying whether the properties of the Higgs boson are those expected from the Standard Model.
The Large Hadron Collider and the planned decade of studies will clearly help in this task. It will however not be sufficient. More powerful colliders are needed, and in fact, this guarantees about fifty years and possibly even a hundred years of exciting physics.
Will we be able to say that the Standard Model is complete after these 100 years? I do not know, but what is clear is that we may discover non Standard Model phenomena on the way, as expected by the conceptual limitations and issues of the Standard Model. This will be addressed in the next blog!
In the meantime, I wish you a wonderful week and let’s hopefully see each other next Monday (otherwise this will be for the first or second Monday of 2022). Please do not hesitate to ask questions and comment. I am here to answer!
Extremely interesting and well-written blog! I recently finished a biography of Einstein that detailed his quest for a unified field theory in the last few decades of his life. No doubt he would be greatly heartened to see that tireless researchers like yourself are on still hard on the trail all these years later!
Thanks for passing by!
Unification is one of the bit motivation to go beyond the Standard Model of particle physics (and is therefore a big topic as it was already decades ago). I was planning to mention a few things about it in my next blog, in particular the fact that we do not only try to unify the fundamental forces, but also matter. In this way the different particles will only be different facets of a single entity. The major problem is that the most naive attempts fail (too easy would not be funny).
It's a difficult subject to tackle, especially like laymen like myself, so I can really appreciate you laying it out in such a clear fashion. Looking forward to your next blog on the subject!
Thank you for these very nice words!
Your content has been voted as a part of Encouragement program. Keep up the good work!
Use Ecency daily to boost your growth on platform!
Support Ecency
Vote for new Proposal
Delegate HP and earn more
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (80% of the curation rewards are returned).
Please consider including @stemsocial as a beneficiary to get a stronger support.
Congratulations @lemouth! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s):
Your next target is to reach 64000 upvotes.
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPSupport the HiveBuzz project. Vote for our proposal!
I don't have much opinion on the holographic principle as I haven't studied these carefully. This is in fact quite far from what I am working on (high-energy physics is a vast territory). I know some physicists work on this, which is good as we need to be pragmatic and consider any options (as long as these options are not excluded by data).
For the many-world interpretation, this is an alternative way to interpret quantum mechanics. As above, it has not be proven wrong although some see flaws in it. I have personally... no opinion. I feel comfortable with the standard Copenhagen interpretation (that allows to explain data very well). I know of course that other possibilities exist, and that they have at the end of the day pros and cons.
PS: Sorry for not providing any clear answer, but I don't have any here. I know where my personal limits are.
It is definitely not a bullshit theory! But it is too early to say whether it will last.