¡Hola amigos de Hive blog!
Reciban un cordial saludo.
En mis publicaciones anteriores expliqué como obtener las ecuaciones equivalentes que permiten la simplificación de circuitos cuya estructura esta dada por asociaciones en serie o en paralelo de sus elementos pasivos conocidos como capacitores, resistencias e inductores.
Sin embargo, existen situaciones donde el circuito eléctrico no presenta una configuración en serie o en paralelo, lo que impide la aplicación de las ecuaciones definidas para esas configuraciones haciendo necesaria la aplicación de otros métodos que permitan obtener la Impedancia total de la red eléctrica.
Con el fin de proporcionar otras herramientas que permitan fortalecer y consolidar nuestros conocimientos en el análisis de circuitos, analizaremos en este trabajo el método de simplificaron de circuitos conocido como transformación delta – estrella o estrella-delta, debido a la configuración de sus elementos. Este método permite a partir de transformaciones sucesivas la obtención de la impedancia total de una red en el que sus elementos no están agrupados en serie o en paralelo, siendo además un método valido para cualquier red sea de tipo monofásica o trifásica.
Fundamento Teórico
Para facilitar nuestro análisis consideraremos una red eléctrica netamente resistiva, tomando en cuenta que el método también puede ser aplicado a una red eléctrica con elementos capacitivos o inductivos.
En las siguientes figuras se muestran las configuraciones de los circuitos eléctricos estrella y delta.
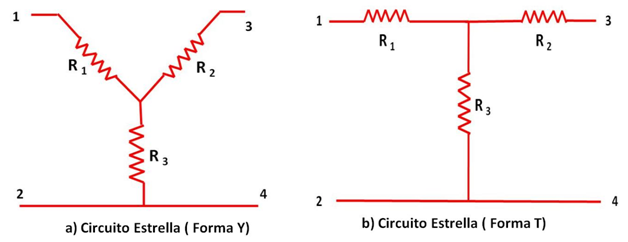
(Elaborada por @lorenzor)
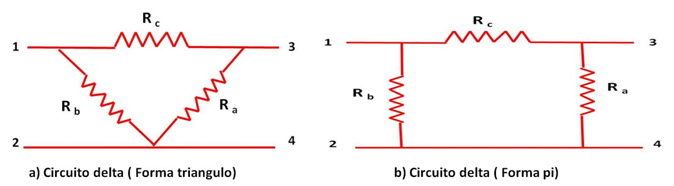
(Elaborada por @lorenzor)
La transformación de un circuito delta a un circuito estrella o viceversa depende de la estructura del circuito en la que el analista deberá decidir cual de las transformaciones es mas conveniente, de tal forma que la transformación escogida lo conduzca a una configuración mas simple, bien sea una asociación en serie o en paralelo.
En el siguiente análisis desarrollaremos la transformación de un circuito a otro basados en los análisis de impedancia entre los extremos de ambas configuraciones y la equivalencia existente entre ellas.
Transformación de un circuito Delta a Estrella
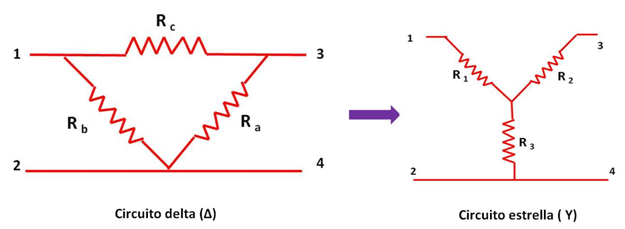
(Elaborada por @lorenzor)
Para transformar un circuito delta a un circuito estrella es necesario la obtención de las resistencia R1, R2 y R3 a partir de los valores de resistencias Ra, Rb y Rc de la estructura delta.
Para obtener las ecuaciones que permiten calcular cada resistencia del circuito estrella (R1, R2 y R3) se igualan las impedancias entre los nodos 1, 2, 3 y 4 dado que estas son iguales en ambas configuraciones.
Nodos 1 - 2
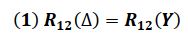
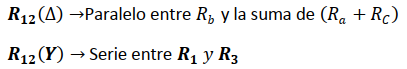
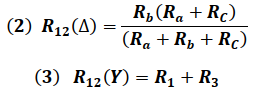
Igualando las impedancia entre los Nodos 1 y 2 de ambas configuraciones se tiene:
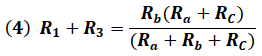
Nodos 1 - 3
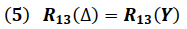
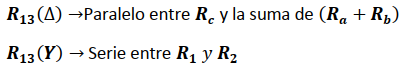
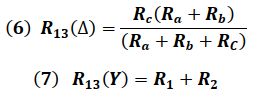
Igualando las impedancia entre los Nodos 1 y 3 de ambas configuraciones se tiene:
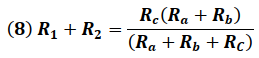
Nodos 3 - 4
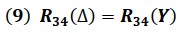
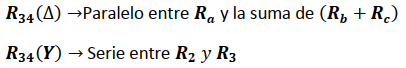
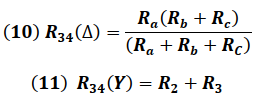
Igualando las impedancia entre los Nodos 3 y 4 de ambas configuraciones se tiene:
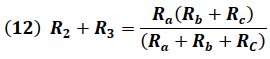
Combinando las ecuaciones (4), (8) y (12) obtenemos:
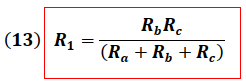
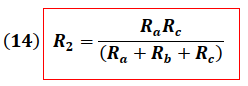
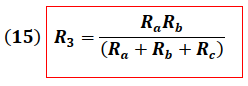
Se puede notar que las expresiones (13), (14) y (15) muestran un patrón en su estructura, lo que permite su obtención de una manera práctica sin la necesidad de realizar su deducción cada vez que sean requeridas o que estas deban ser memorizadas.
Una manera practica de construir estas ecuaciones es colocando el circuito estrella dentro de la estructura delta y derivar a partir de esta figura las resistencias R1, R2 y R3 (Ver Figura 4).
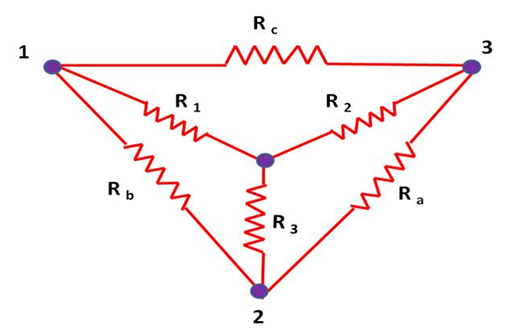
(Elaborada por @lorenzor)
El resultado obtenido en el análisis de impedancia muestra que cada una de las resistencia del circuito estrella (R1, R2, R3) siempre estará dado por el producto de las resistencias laterales ubicadas en el circuito delta, dividido entre la suma de las resistencias que conforman el circuito delta (Ra, Rb, Rc).
En la figura 5 se puede observar que para el caso de la resistencia R1, las resistencias laterales en el circuito delta están dadas por Rb y Rc, de tal modo que según lo enunciado por el método práctico se tiene:
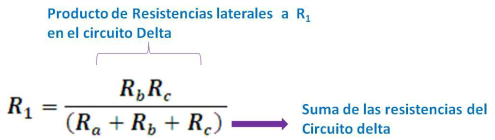
(Elaborada por @lorenzor)
Este método práctico aplica para el resto de las resistencias del circuito estrella y esta validado en el análisis de impedancia desarrollado en nuestro marco teórico, en el que se obtienen las resistencias R1, R2 y R3.
Transformación de un circuito Estrella a Delta
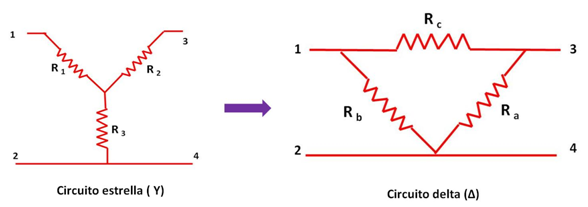
(Elaborada por @lorenzor)
Para transformar un circuito estrella a un circuito delta se deben obtener las resistencias Ra, Rb y Rc a partir de los valores de resistencias R1, R2 y R3 de la estructura delta.
Desarrollando el producto entre las resistencias del circuito estrella dadas por las expresiones (13), (14) y (15) y sumando dichos productos, se obtiene:
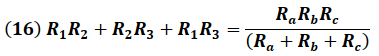
Dividiendo la expresión (16) entre cada resistencia del circuito estrella (R1, R2 y R3) definidas por las ecuaciones (13), (14) y (15), se obtiene:
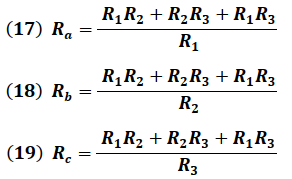
En esta transformación se observa nuevamente un patrón en la estructura de las ecuaciones, lo que permite que puedan obtenerse de manera práctica cuando estas sean requeridas.
Del patrón observado se concluye que cada resistencia del circuito delta estará dada por la sumatoria de todos los pares de productos posibles del circuito estrella, dividido entre la resistencia del circuito estrella que esta ubicada en el lado opuesto.
En la siguiente Figura se ilustra el método práctico para la obtención de una de las resistencias del circuito delta (Ra) a partir de los valores de resistencias del circuito estrella.
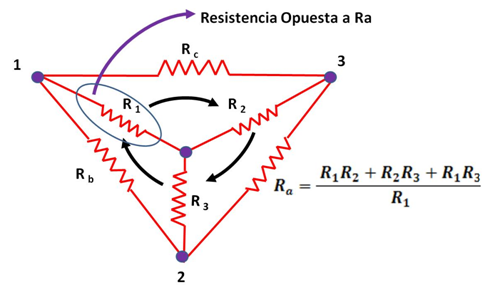
(Elaborada por @lorenzor)
Ejercicio Práctico y Simulación
Determinar la corriente total “i” del siguiente circuito.
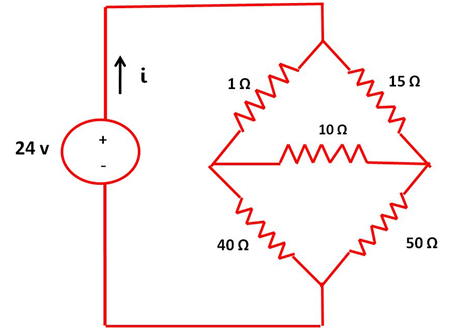
Solución
Análisis Teórico
Para la obtención de la corriente “i” simplificaremos el circuito utilizando en método de transformación delta a estrella en la rama inferior delta formada por las resistencias de 40 Ω, 10 Ω y 50 Ω.
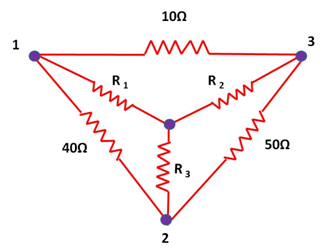
Usando las ecuaciones (13), (14) y (15) obtenidas en nuestro análisis teórico se tiene que:
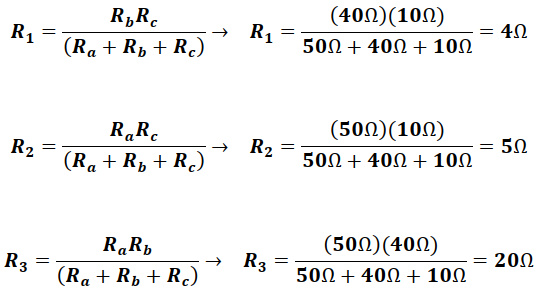
De los resultados obtenidos el circuito toma la forma:
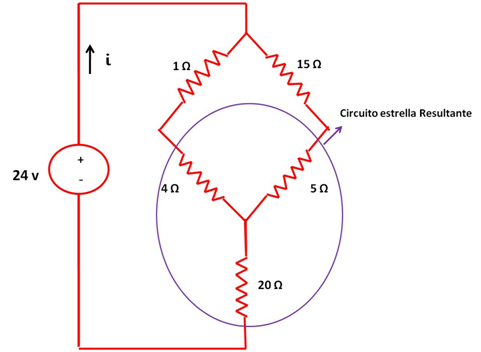
Luego de la transformación, se puede notar la asociación en serie entre las resistencias de 1Ω y 4 Ω y entre las resistencias de 15 Ω y 5 Ω.
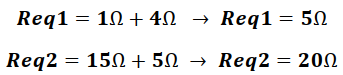
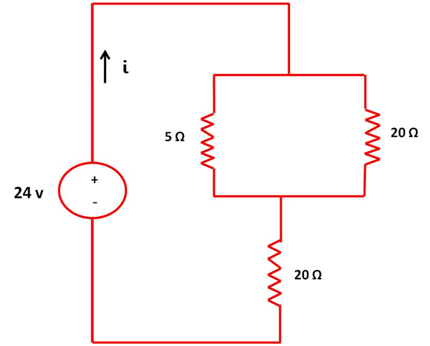
Finalmente, para obtener la resistencia total del circuito se desarrolla el paralelo entre las resistencias de 5Ω y 20Ω, lo que genera una resistencia equivalente que estará en serie con la resistencia de 20Ω.
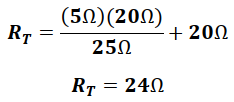
De la ley de Ohm tenemos que:
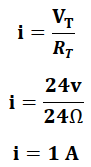
Simulación
Con el objeto de validar el análisis teórico realizado en este trabajo y los resultados obtenidos en el circuito ejemplo en la siguiente simulación, realizada con el simulador de circuitos Proteus version 8, se puede observar que la corriente eléctrica generada por la fuente y la resistencia total del circuito, registradas por el amperímetro y el Ohmímetro, esta en total concordancia con los valores teóricos obtenidos.
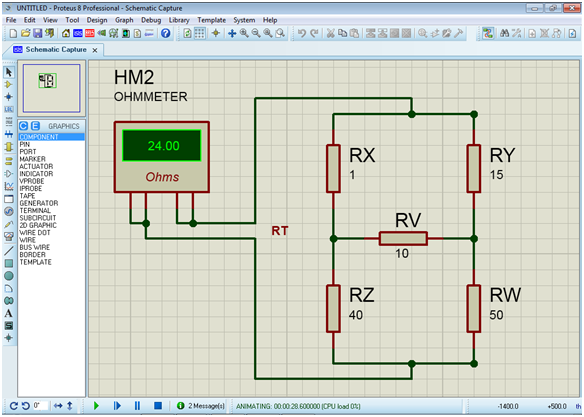
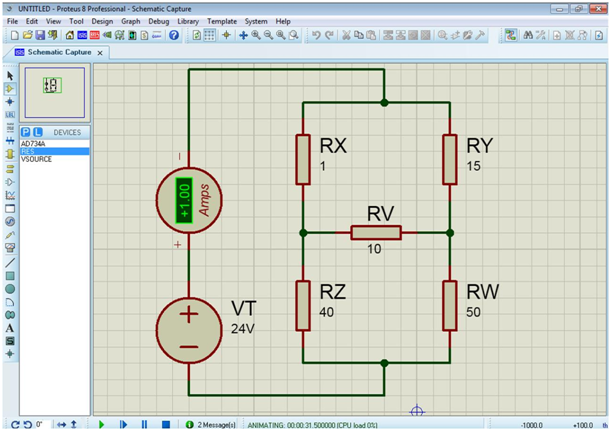
Del análisis realizado se puede apreciar la validez del método de transformación delta-estrella, siendo esta una herramienta útil en el análisis de redes eléctricas, ya que permite la simplificación de un circuito eléctrico facilitando además, la obtención de los parámetros de voltaje y corriente.
Gracias por leer mi publicación, espero que el análisis realizado en este trabajo permita fortalecer y consolidar sus conocimientos en el estudio de las redes eléctricas.
Si tienes alguna duda, pregunta o sugerencia deja tus comentarios y con mucho gusto te responderé.
Referencias
- Circuitos Eléctricos. James W. Nilson. Cuarta edición. Addison-Wesley Iberoamericana.
- Física Vol. II Campos y ondas. Marcelo Alonso, Edward J. Finn. Fondo Educativo Interamericano, S.A.
- Física para ingeniería y ciencias Vol.2 Tercera Edición / Hans C. Ohanian, John T. Markert.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app
app and including @stemsocial as a beneficiary to get a stronger support.
Hola @lorenzor magistral su explicación en el análisis de redes eléctricas con la transformación delta – estrella o estrella-delta, acompañado de la simulación. Gracias
Saludos @alfonsoalfonsi. Gracias por su visita y comentario positivo. Las simulaciones en la situación actual son una herramienta alternativa muy útil para validar los resultados teóricos. Gracias.