¡Hola amigos de Hive blog!
Reciban un cordial saludo.
La combinación de elementos pasivos, tales como resistores y capacitores, es una herramienta útil que permite la simplificación de una gran variedad de circuitos constituidos con más de uno de estos componentes a un circuito equivalente en el que una única resistencia o capacitancia, según sea el caso, representa el valor total de la combinación, lo que facilita además la obtención de la corriente y el voltaje absorbido por toda la red.
Ahora bien, de la misma forma que en una red eléctrica netamente resistiva o capacitiva es posible obtener la resistencia equivalente o la capacitancia equivalente de la red, en un circuito netamente inductivo donde sus elementos estén asociados en serie o paralelo es también posible obtener la inductancia equivalente de dicha red.
En este artículo realizaremos el análisis de una red eléctrica netamente inductiva donde obtendremos, a partir de los fundamentos físicos y matemáticos que gobiernan el comportamiento de un inductor y los principios inherentes a la combinación en serie y paralelo de elementos pasivos, las ecuaciones equivalentes de una combinación en serie o paralelo de una red inductiva.
Fundamento teórico
Combinación de Inductores en paralelo
En la configuración que se muestra en la figura 1 se tiene un arreglo de inductores en paralelo en el que es posible obtener la inductancia equivalente del circuito, cuyo valor representa la inductancia total de dicha combinación.
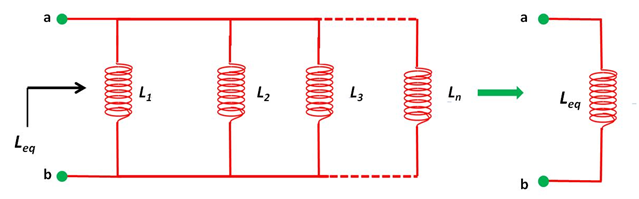
(Elaborada por @lorenzor)
Para obtener la Inductancia equivalente o total del arreglo en paralelo aplicaremos una diferencia de potencial entre los extremos de la combinación (puntos a y b) y analizaremos la distribución de la corriente eléctrica que se establece en el circuito (Ver figura 2).
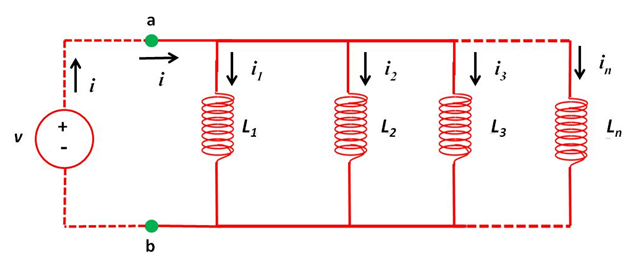
(Elaborada por @lorenzor)
Debido a que en una combinación en paralelo la corriente eléctrica es divida, se tiene que:
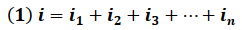
De la ley de Faraday, se tiene que el voltaje en el inductor es directamente proporcional a la variación de la corriente, matemáticamente es expresada de la forma:
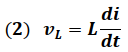
L → Inductancia (constante de proporcionalidad) (Henry)
VL → Fuerza electromotriz (Voltaje en el inductor) (Voltio)
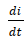 → Variación temporal de la Corriente eléctrica (A/s)
→ Variación temporal de la Corriente eléctrica (A/s)
Despejando "i" de la ecuación (2) tenemos:
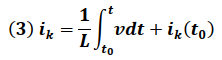
Condición inicial (Valor inicial) 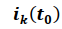 →
→
Debido a que en un circuito en paralelo la diferencia de potencial en cada elemento es la misma, se tiene que:
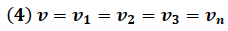
Considerando que el voltaje en una combinación en paralelo es el mismo para cada uno de los elementos, la sustitución de la ecuación (3) en la expresión (1) nos conduce a la relación:
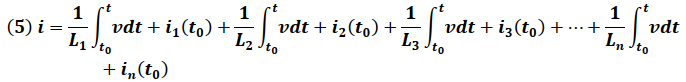
Simplificando obtenemos:
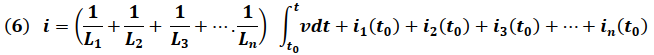
Siendo que la simplificación de la red en paralelo de inductores nos lleva a un inductor equivalente, la estructura final del circuito estará dada por la siguiente configuración:
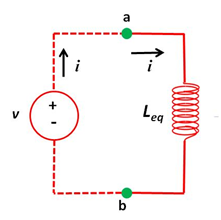
(Elaborada por @lorenzor)
Donde la corriente eléctrica del elemento resultante o equivalente estará definida por la expresión:
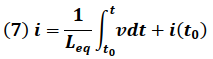
Igualando (6) y (7) se tiene que:
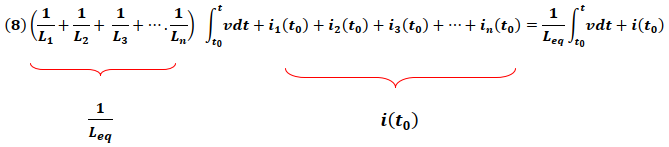
De la expresión (8) se concluye que la inductancia equivalente de la asociación en paralelo está dada por:
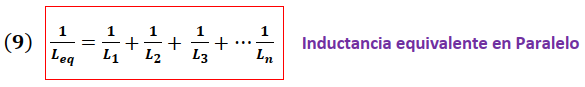
Combinación de Inductores en Serie
De igual forma que en una asociación en paralelo, en una combinación de inductores en serie como el que se muestra en la figura (4), es posible obtener una inductancia equivalente en el que esté representada la inductancia total de la red.

(Elaborada por @lorenzor)
La aplicación de una diferencia de potencial a la combinación en serie de inductores establece una corriente eléctrica en el circuito que es la misma para cada uno de los elementos que la constituye, mientras que el voltaje aplicado es distribuido entre los inductores de la red (Ver Figura 5).
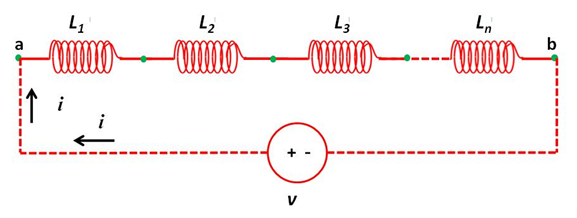
(Elaborada por @lorenzor)
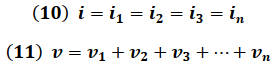
Sustituyendo (2) en (11) se obtiene:
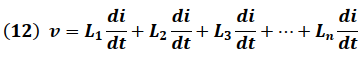
Simplificando:
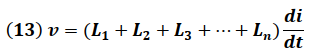
La simplificación de la estructura en serie nos conduce a un circuito equivalente cuya configuración tendrá la siguiente forma:
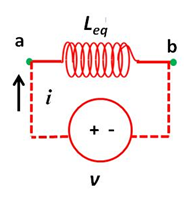
(Elaborada por @lorenzor)
Dado que:
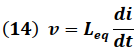
Igualando (13) y (14) tenemos:
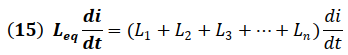
De la expresión (15) se desprende que:
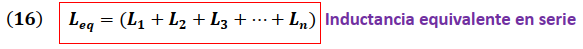
Ejercicio
Determine en la red que se muestra en la figura (7) la inductancia equivalente.
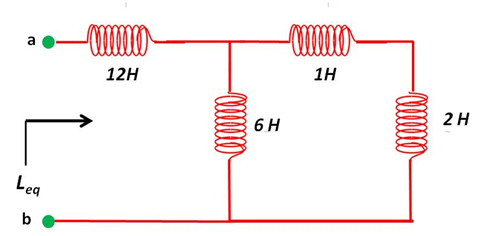
(Elaborada por @lorenzor)
Solución
Para la determinación de la inductancia equivalente del circuito se deben identificar las las combinaciones que satisfacen los principios de una combinación en serie o en paralelo.
Se puede observar que los inductores de 1 H y 2 H cumplen con una combinación en serie, dado que la corriente eléctrica que fluye por cada uno es la misma.
Usando la ecuación de la inductancia equivalente en serie dada por la expresión (16) se tiene:
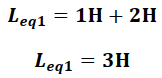
De la primera simplificación se obtiene el circuito que se muestra en la figura 8.
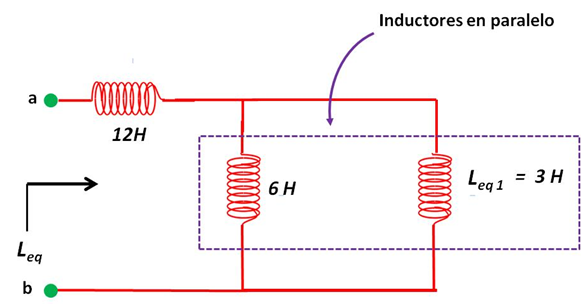
(Elaborada por @lorenzor)
Combinando en paralelo los inductores de 6 H y Leq1= 3H de la ecuación (9), se obtiene:
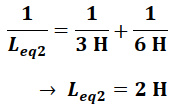
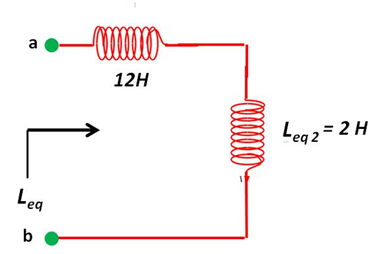
(Elaborada por @lorenzor)
Finalmente, los inductores de 12H y Leq2 = 2 H se agrupan en serie generando una inductancia equivalente dada por:
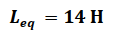
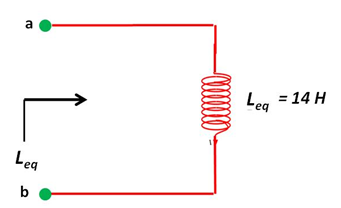
(Elaborada por @lorenzor)
Del análisis realizado se puede apreciar que es posible simplificar a través del método de reducción sucesiva de serie y paralelo una red eléctrica inductiva, permitiendo este proceso la obtención de una forma mas simple de los parámetros de voltaje y corriente absorbidos por la red.
Gracias por leer mi publicación, espero que el análisis desarrollado en este trabajo permita fortalecer y consolidar sus conocimientos en el estudio de las redes eléctricas.
Si tienes alguna duda, pregunta o sugerencia, deja tus comentarios y con mucho gusto te responderé.
Referencias
- Circuitos Eléctricos. James W. Nilson. Cuarta edición. Addison-Wesley Iberoamericana.
- Introduction To Electromagnetic Fields Third Edition / Clayton R. Paul, Keith W. Whites, Syed A. Nasar
- Física Vol. II Campos y ondas. Marcelo Alonso, Edward J. Finn. Fondo Educativo Interamericano, S.A.
- Física para ingeniería y ciencias Vol.2 Tercera Edición / Hans C. Ohanian, John T. Markert.
- Teoría electromagnética. Willian H. Hayt, Jr., John A. Buck. Séptima edición. McGraw Hill.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app
app and including @stemsocial as a beneficiary to get a stronger support.
Me encanta aprender sobre estas cosas mi unico problema es que no son lo mismo comparados con la vida real, quise aprender a armar circuitos y nunca me salieron.