¡Hola amigos de Hive Blog!
Reciban un cordial saludo.
En mi publicación anterior analizamos los fundamentos físicos y matemáticos que permiten la obtención de la resistencia equivalente de un circuito en el que sus elementos resistivos poseen una asociación en serie o en paralelo.
En esta oportunidad se mostrará como obtener, a partir de la ley de Kirchhoff de los voltajes, la resistencia equivalente de un circuito en el que sus resistencias o impedancias no tienen una combinación en serie o en paralelo definida.
Si bien el método de reducción por serie y paralelo permite de manera simple la obtención del valor equivalente de la resistencia de la red donde dichas combinaciones están presentes, el método de Kirchhoff también ofrece una forma rápida y sencilla en la obtención de la resistencia equivalente de circuitos donde las resistencias que lo constituyen tengan o no una combinación definida, convirtiéndolo de esta forma en un método general en la obtención de dicho valor.
A continuación, se muestra un circuito eléctrico en el que las resistencias que lo forman no tienen una combinación en serie o en paralelo.
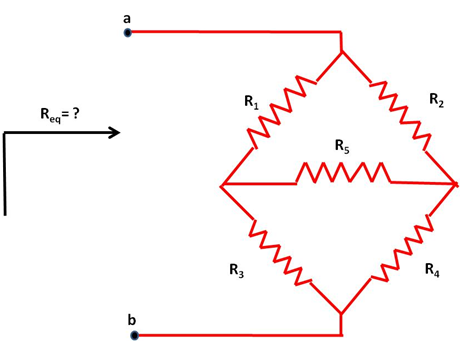
(Elaborada por @lorenzor)
Para la determinación de la resistencia equivalente de la asociación mostrada en el circuito usando las leyes de Kirchhoff, se debe iniciar energizando la red con un valor arbitrario de voltaje o corriente, lo cual conducirá a una relación entre los valores totales de voltaje y corriente, que serán directamente proporcional al valor de la resistencia total del circuito, tal y como lo establece la Ley de Ohm (Ver figura 2).
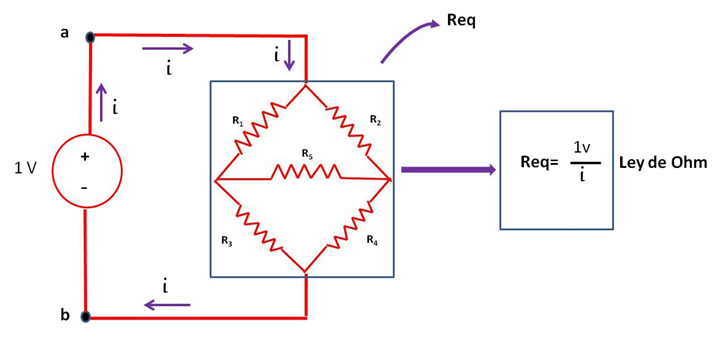
(Elaborada por @lorenzor)
De esta forma, se puede apreciar que la resistencia total o equivalente de la red quedará determinada una vez se obtenga la corriente total “i ” del circuito.
En el siguiente circuito se muestra la distribución de las corrientes de malla que permiten aplicar las leyes de Kirchhoff de los voltajes.
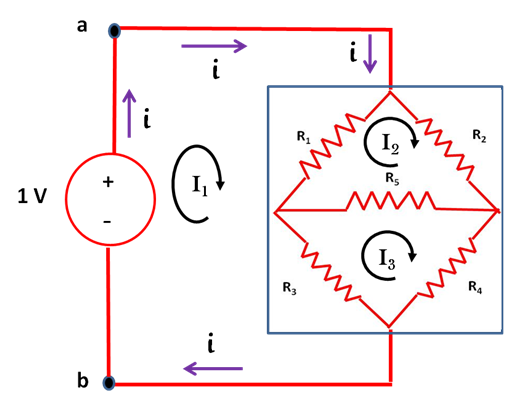
(Elaborada por @lorenzor)
De la ley de Kirchhoff de los voltajes, se obtiene en cada una de las mallas del circuito las siguientes ecuaciones:
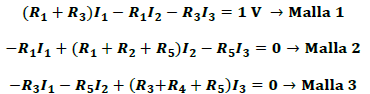
La solución del sistema de ecuaciones permite obtener las corrientes en cada una de las mallas y en la que el valor de la corriente "I1" representa la corriente “i” requerida para la determinación de la resistencia total del circuito.
En el siguiente ejemplo determinaremos el valor de la resistencia total o equivalente de una red eléctrica con valores conocidos de sus elementos resistivos.
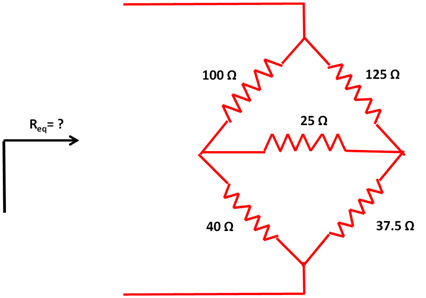
(Elaborada por @lorenzor)
Solución
Aplicando un voltaje arbitrario a la red (1V) y definiendo las corrientes de malla en el circuito se tiene:
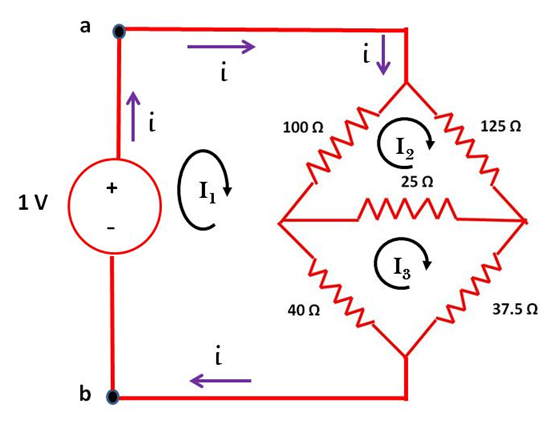
De la ley de Kirchhoff de los voltajes se tiene:
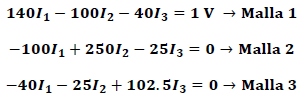
De La solución del sistema de ecuaciones se tiene:
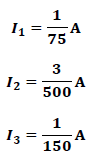
Dado que 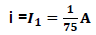 :
:
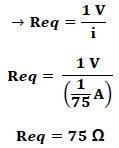
De esta forma se puede apreciar que a partir de la ley de Kirchhoff de los voltajes es posible obtener la resistencia equivalente de una red eléctrica, donde sus elementos constituyentes no poseen una asociación en serie o en paralelo.
Si bien existen otros métodos de simplificación de redes eléctricas en los que sus resistencias no tienen una combinación serie-paralelo, el método de Kirchhoff propuesto en este trabajo ofrece una rápida solución a este tipo de redes.
En una próxima publicación, abordaremos otros métodos para la obtención de la resistencia equivalente de circuitos eléctricos cuyas configuraciones son conocidas como circuitos triangulo – estrella  .
.
 .
.Referencias
- Circuitos Eléctricos. James W. Nilson. Cuarta edición. Addison-Wesley Iberoamericana.
- Introduction To Electromagnetic Fields Third Edition / Clayton R. Paul, Keith W. Whites, Syed A. Nasar
- Física Vol. II Campos y ondas. Marcelo Alonso, Edward J. Finn. Fondo Educativo Interamericano, S.A.
- Física para ingeniería y ciencias Vol.2 Tercera Edición / Hans C. Ohanian, John T. Markert.
- Teoría electromagnética. Willian H. Hayt, Jr., John A. Buck. Séptima edición. McGraw Hill.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app
app and including @stemsocial as a beneficiary to get a stronger support.
Congratulations @lorenzor! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s) :
Your next payout target is 2000 HP.
The unit is Hive Power equivalent because your rewards can be split into HP and HBD
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPCongratulations @lorenzor!
You raised your level and are now a Minnow!