¡Hola amigos de Hive Blog!
Reciban un cordial saludo.
En este artículo analizaremos la condicion bajo la cual un cuerpo rígido permanece en equilibrio estático rotacional cuando sobre el actúan un conjunto de fuerzas.
El equilibrio de un cuerpo plantea el hecho de que el objeto sobre el que actúan las fuerzas se encuentra en reposo o que la velocidad de su centro de masa es constante.
En el equilibrio estático se considera el caso especial de la ausencia de velocidad, tanto del centro de masa como de la velocidad angular respecto a un eje de rotación.
En la práctica, el equilibrio estático es de gran interés en distintas áreas de la ingeniería entre las que se destacan la ingeniería civil, la Ingeniería mecánica y la arquitectura, las cuales basadas en los principios de equilibrio, han permitido la construcción de puentes, edificios y sistemas de grúas con aplicaciones importantes en el desempeño de los huesos y articulaciones de seres vivos.
Fundamentos teóricos
Para los objetos puntuales, la condición de equilibrio estático se obtiene cuando la fuerza neta que actúa sobre el cuerpo es cero, tal y como lo establece la siguiente ecuación:
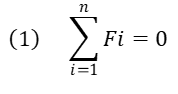
En el caso de un cuerpo extendido (Rígido), la condición de equilibrio estático debe cumplir una segunda condición, la cual está asociada al momento de torsión.
En la siguiente imagen se muestra la aplicación de una fuerza sobre un punto P de un cuerpo rígido respecto al punto de referencia O.
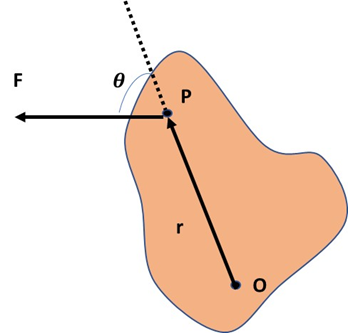
(Elaborada por @lorenzor en Powerpoint)
El momento de Torsión de la fuerza F respecto al punto O esta dado por la expresión:
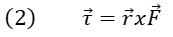
Se puede observar que el efecto que la fuerza F genera sobre el objeto es de una rotación respecto al eje que pasa por el punto O.
Por definición, el momento de torsión está relacionado con su momento de inercia "I" y su aceleración angular"α" a través de la ecuación:
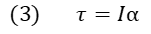
Dado que la condición de equilibrio total del cuerpo (Traslacional y rotacional) exige que la velocidad lineal “vCM” y velocidad angular “ω” sean nula, esto implica a su vez que las aceleraciones respectivas también lo sean.
De tal forma que para garantizar el equilibrio estático rotacional se debe cumplir que la aceleración angular sea cero (α=0).
Con esta condición se establece en forma general que en equilibrio estático rotacional el momento de torsión neto sobre el cuerpo es nulo, tal y como se muestra en la siguiente ecuación:
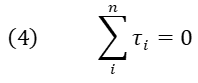
Ejemplo
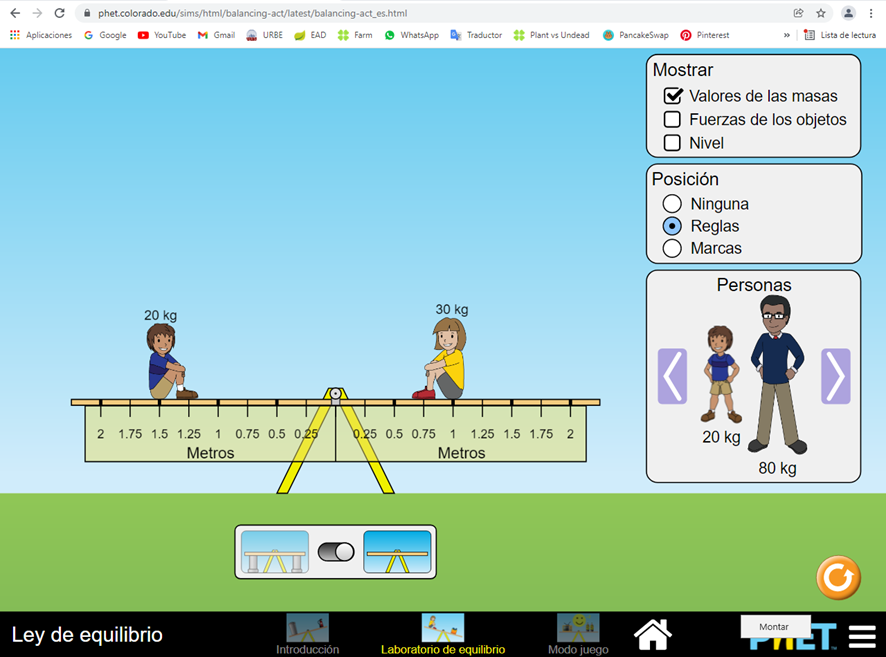
Para ilustrar la condición de equilibrio estático rotacional realizaremos un análisis teórico y practico utilizando el simulador PhET, para determinar la posición de equilibrio en la que un segundo niño tendría que ubicarse sobre un tablón, cuyo centro de gravedad está colocado sobre el soporte del sistema que se muestra en la imagen.
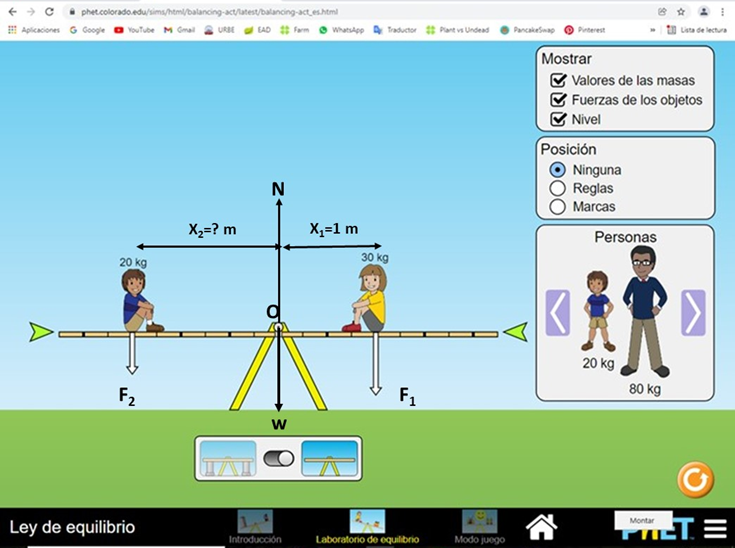
Para facilitar el análisis se debe elegir de forma conveniente un eje de rotación respecto al cual se pueda obtener el momento de torsión total que actúa sobre el cuerpo.
Dada que la elección del eje es arbitraria, se selecciona de tal forma que los cálculos se simplifiquen.
En nuestro sistema, el punto de referencia es tomado en el punto de pivote identificado como punto “O”.
Con la elección del eje de rotación en el punto “0”, los momentos de torsión debido a la fuerza normal (Reacción del soporte sobre el tablón) y el peso del tablón “w” son nulos, dado que los respectivos vectores posición de esas fuerzas respecto al punto “O” son nulos
, lo que implica que el momento total esta determinado por los momentos de torsión generados por los pesos de cada niño, tal y como se muestra en las siguientes ecuaciones.
, lo que implica que el momento total esta determinado por los momentos de torsión generados por los pesos de cada niño, tal y como se muestra en las siguientes ecuaciones.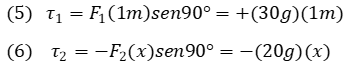
Es importante acotar que, en nuestro análisis, el momento de torsión ha sido considerado positivo para la fuerza F1 (peso del niño en la posición 1), cuya tendencia de giro es en el sentido de las agujas del reloj y negativo para la fuerza F2 (peso del niño en la posición 2), con una tendencia de giro en sentido contrario a las agujas del reloj.
Aplicando la condición de equilibrio estático rotacional dada por la expresión (4) tenemos:
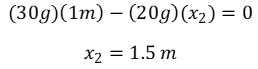
Para validar el resultado obtenido, en la siguiente imagen se muestra la posición de equilibrio obtenida a partir del simulador PhET, donde podemos observar que dicha posición está en concordancia con el resultado en nuestro análisis teórico, validando de esta forma los principios y fundamentos aquí expuestos.
Gracias por leer mi publicación, espero que el análisis realizado en este trabajo permita fortalecer y consolidar sus conocimientos en el estudio del equilibrio estático rotacional de un cuerpo.
Si tienes alguna duda, pregunta o sugerencia deja tus comentarios y con mucho gusto te responderé.
Referencias
- Física para Ciencias e Ingeniería. Fishbane, Gasiorowicz, Thornton. Volumen I. Prentice Hall.
- Física para la Ciencia y la Tecnología. Tipler Mosca. Volumen 1: Mecánica. Oscilaciones y ondas. Termodinámica. 5a edición. Editorial Reverté.
- Física para Ciencias e Ingeniería. Raymond A. Serway, Robert J. Beichner. 5a edición. Tomo I. McGraw-Hill.
- Física Universitaria. Sears Zemansky, Young Freedman. 9na edición. Volumen 1. Addison Wesley Longman.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (80% of the curation rewards are returned).
Please consider including @stemsocial as a beneficiary to get a stronger support.