Hello math bugs (🐞) & hivers(🐝)
I hope you are strong & stout and doing great in life.
Here is another problem on similarity. The problem says: There are two poles of 15m and 10m height, standing vertically on the ground. If tops (A,D) are connected to the bottoms(B,C), the two line segments thus made cut at a point called p. You have to find out the height of PQ.
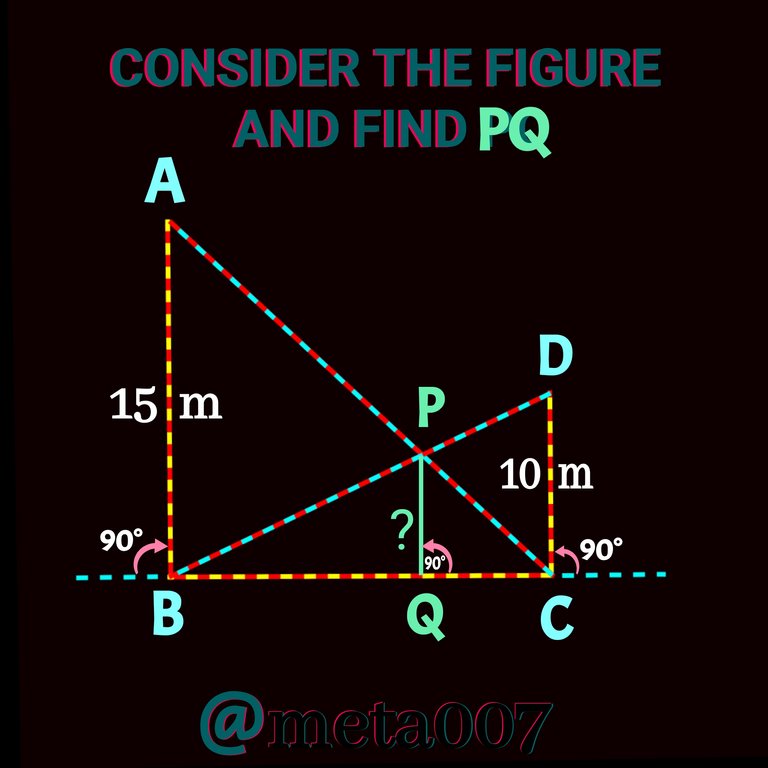
The problem is very simple.There is a relation between AB, CD and PQ. Which is given by:
1/(AB) + 1/(CD)= 1/(PQ)
The values of AB and CD are given. Solving the avobe equation we can easily find out the value of PQ.
Solving farther we can say PQ=(AB×CD)/(AB +CD)
So PQ = (15×10)÷(15+10) = 150/25 = 6 [ cm]
Concept we need to know:
You should know one thing that parallel line segments in a triangle always divide other non parallel sides into same ratio. The point may not be cleared to you. Let's check a figure to figure it out.
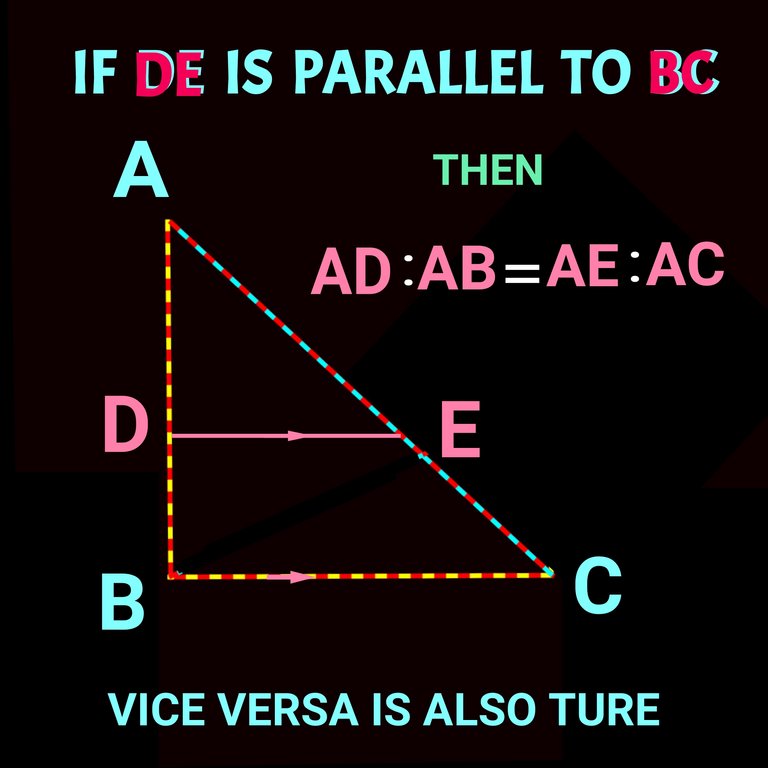
Note: In that case we can aslo write AD: BD = AE: CE.
It is so because, in the above figure, both of the triangles (∆ADE and ∆ ABC) are similiar as their three angles are equal in measurement.
Let's now prove how 1/(AB) + 1/(CD) = 1/(PQ)
In the question also in follwoing figure you can see AB and PQ are parallel. So, we can use similarity in ∆ABC and ∆PQC. Let's check it in the follwoing figure:
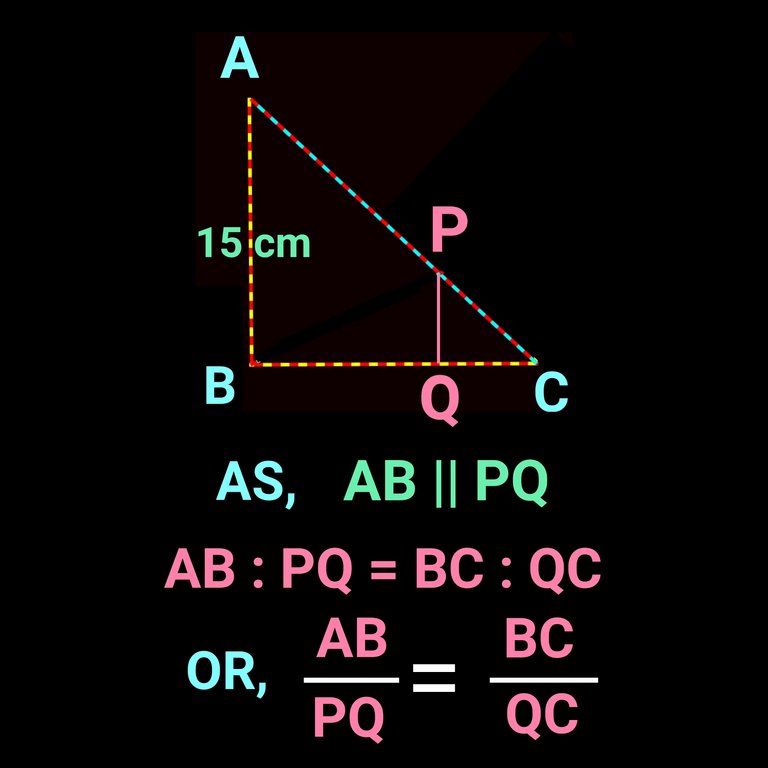
Again , in the same way as CD parallel to PQ, we can use similarity in ∆BCD and ∆BQP. We get the following:
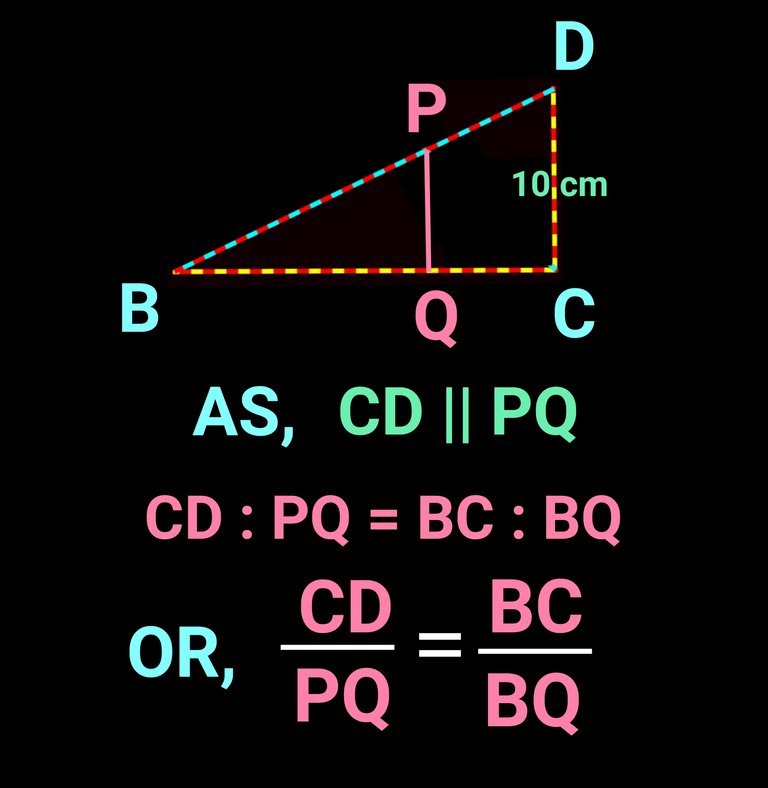
Now, from both of the conclusions in the above two figures, we can derive the required formula. Let's find how AB and CD can be written and then If we add the reciprocal of AB and CD, we get our formula mentioned and used above to find our answer i.e the value of PQ. Let's check the following figure how it can be done:

Now let's add the above two equation to see what we get:
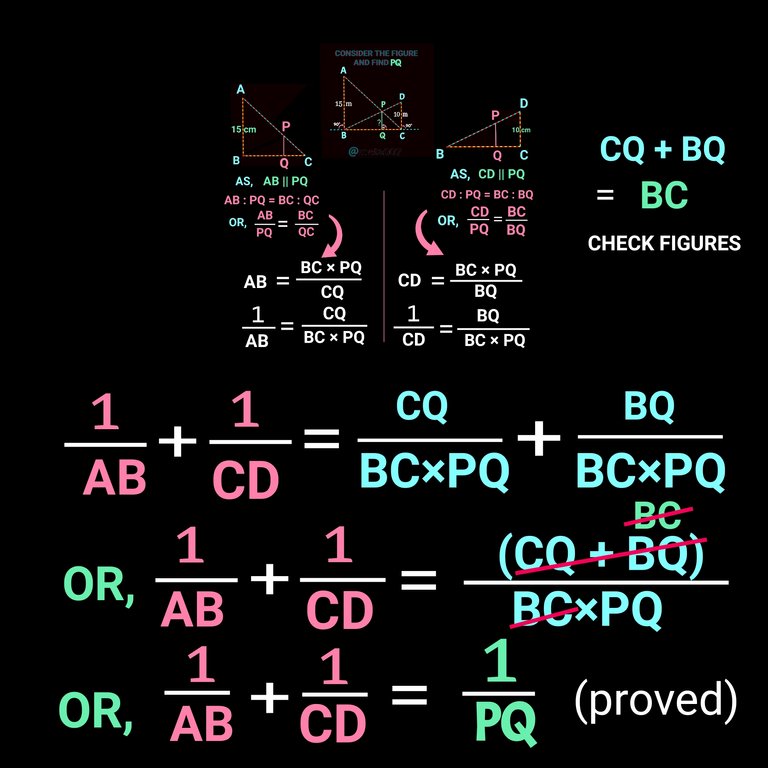
Bravo! We made it.
If you have problem to use similarity, feel free to check my previous post on it here: similarity on right triangle.
🎤🎤 All the figures used here are mdae by me. Figures may not be accurate in measurement; try considering the given data only. If there is any silly mistakes, please excuse me for that and try ignoring it.
I hope you like today's work.
Thank you so much for coming around.
Have a nice day.
All is well.
Regards: @meta007
Post manually reviewed and approved for an Ecency boost. 😊
Thank you so much palomap3
It’s my pleasure!
Yay! 🤗
Your content has been boosted with Ecency Points
Use Ecency daily to boost your growth on platform!
Support Ecency
Vote for new Proposal
Delegate HP and earn more, by @meta007.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
Thanks for including @stemsocial as a beneficiary, which gives you stronger support.
Congratulations @meta007! You have completed the following achievement on the Hive blockchain And have been rewarded with New badge(s)
Your next target is to reach 30000 upvotes.
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPCheck out our last posts: