Cir-Cum-Radius of an equilateral triangle.

[meta007]

Hello math bugs (🐞) and hivers(🐝)
I hope everything is fine and you are having a good time.

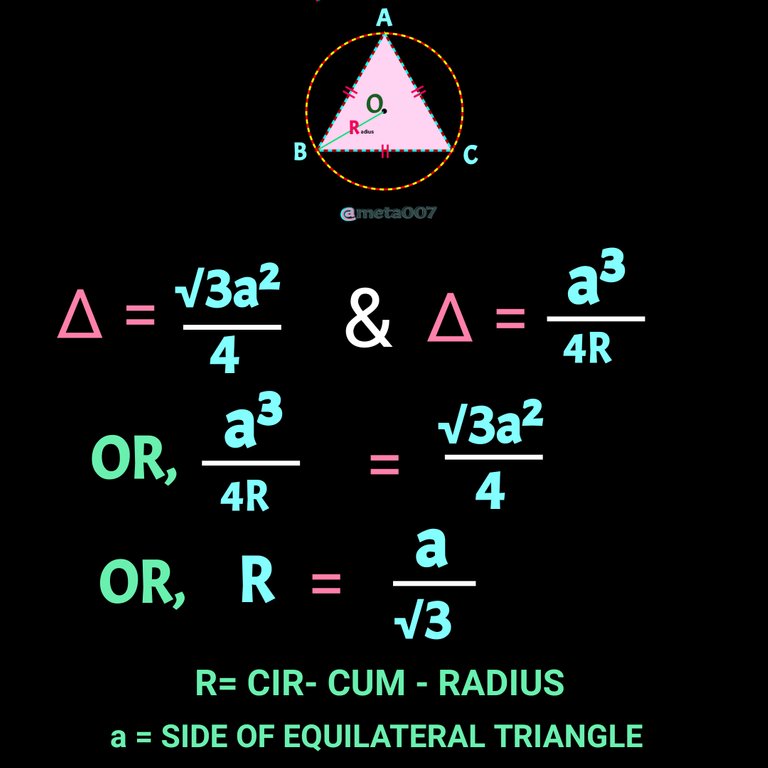
Well come back to another interesting and very important geometric conclusion which is given by R = a/√3 unit, where R means Cir-cum-radius and a is the measurement of am eqilateral triangle, as you can see in the following figure.

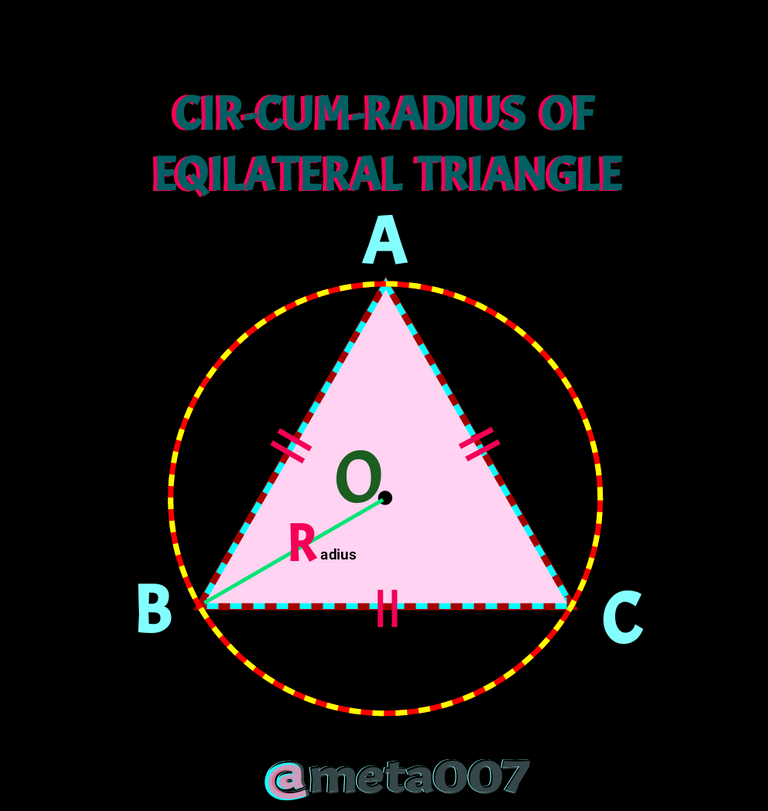
To prove R= a/√3 we gonna need two basic formullae. One of them is given by ∆= √3/4a² uint² and the other one is ∆= abc/4R, here ∆ implies area of the triangle and a,b &c are three sides of a triangle. I am going to proof both of the above formullae I mentioed above and then we will move to today's consideration
R = a/√3

Let's proof first area of an eqilateral triangle is given by ∆= √3/4a²:

There are different ways to find area of a triangle. I am gonna use the basic 1/2×base×height formula and mention the others giving refrence of them as I used or proved in my previous post.

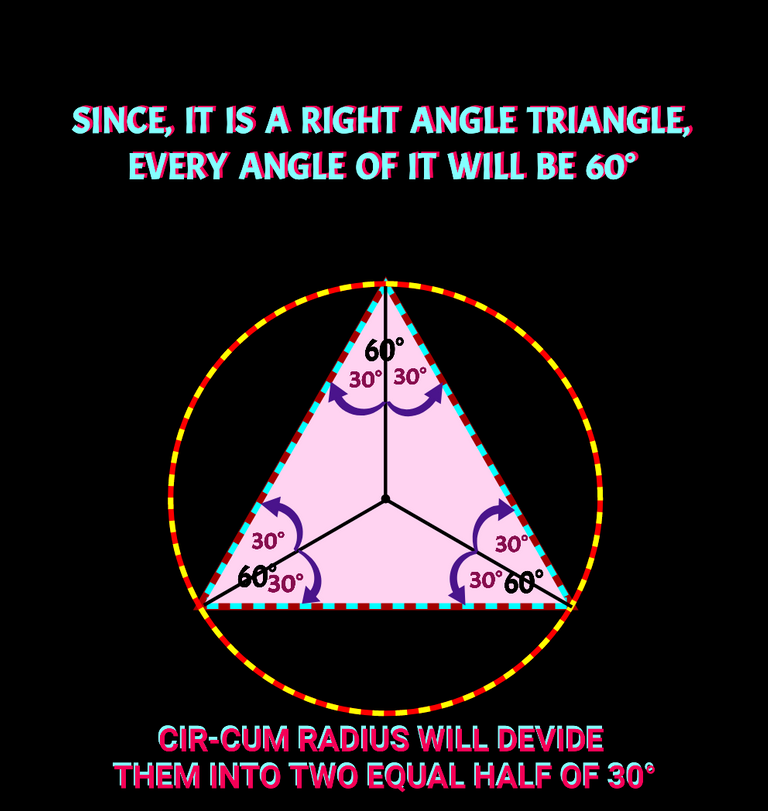
Check, in case of eqilateral triangle, as all sides are equal and so, all angle will also be equal and hence each of the angle be equal to 60° and each raids drawn from vertices will divide each of the angle into two equal half of 30°. As you can see in the following figure.

When the raidus connecting vertices and the centre are produced to the respective sides of the triangle, it will divide and side into two half each half can be assume a/2 unit , as all sides are equal to a as I draw in the following figure.

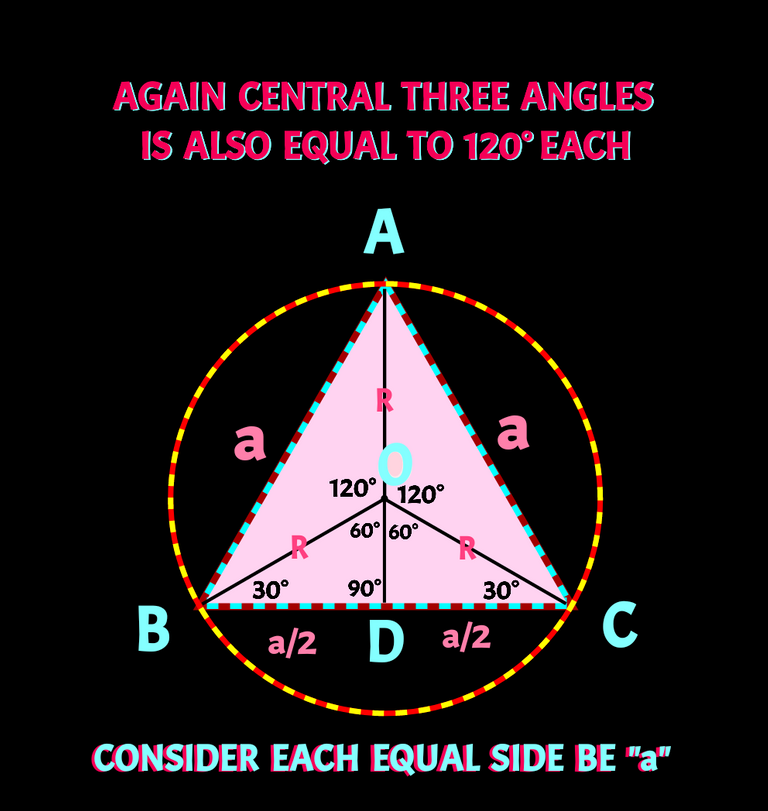
Now from ∆ BCO we can say

Area of ∆BCO = 1/2× BC × DO

For a right triangle of angle 60° ,30° and 90°, the ratio of the sides become √3 : 1 : 2. But here side opposite to angle 60° is a/2. As √3 becomes a/2 , so 1 becomes a/(2√3) and 2 becomes a/√3. But it is not needed here. We just need the base [a/2 ] and the height [a/(2√3)]. Check details in the following figure.

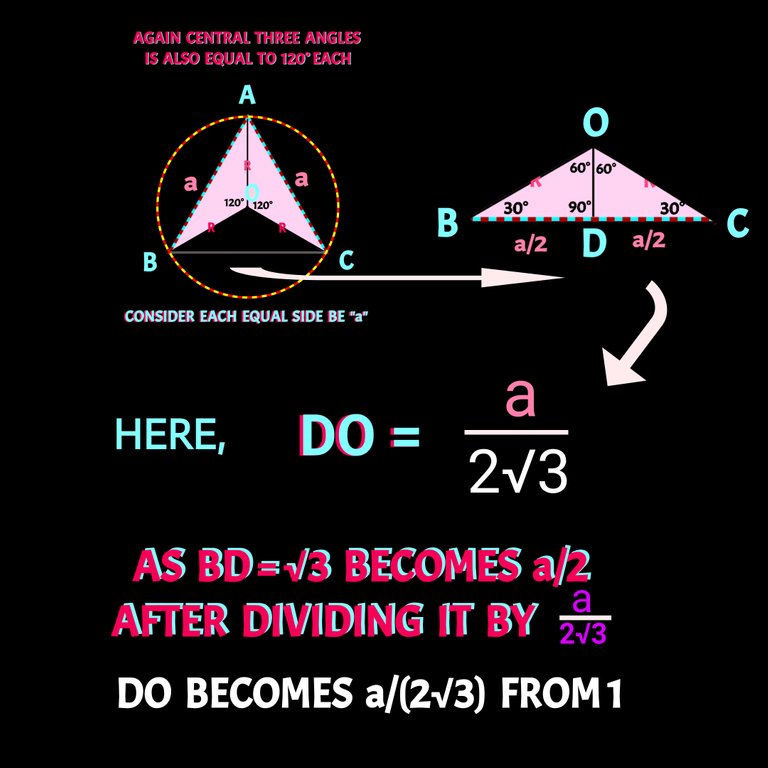
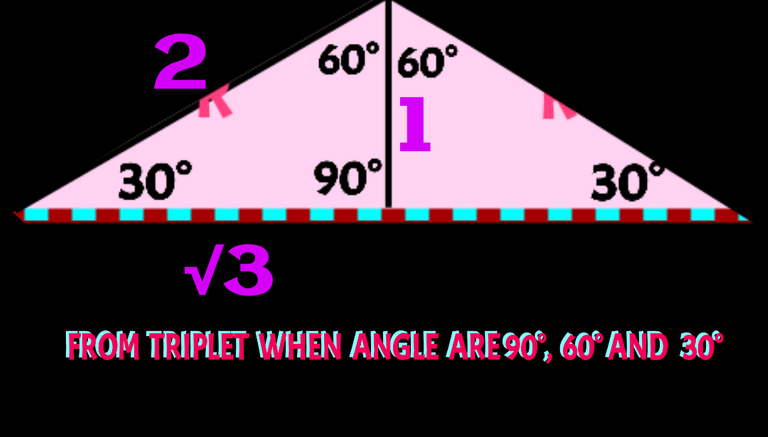
So Area of ∆BCO= 1/2×(a)×a/(2√3)unit²= a²/(4√3) unit²

Hence the are of ∆ ABC becomes = 3 × a² / (4√3 ) unit²
That means Ar ∆ ABC= (√3a²)/4

We can use 1/2× product of two side× sin60° to calculate the area. Check details here

We can also use heron's formulla.

So We got the first formula And which is Ar ∆ABC = (√3a²)/4 unit²

I allready proved in my previous post that Area of a triangle can be writen as ∆ = abc/4R , check it here

As this is equlaterl triangle, we can use it the following way.

Area of triangle = (abc)/ (4R) unit²
Here Ar of ∆ ABC = a³/4R , as three sides are equal.

Now, if we compare this two area , we can solve for R very easily . It will like (√3a²)/4 = a³/4R. If we calculate farther , we can day R = a/√3. Check details in the following figure.

All the figure are made be myself. There may be some silly mistakes while making those figures .please try to ignore them and consider the given data only.

I hope you find my post interesting and effortful. Thank you so for visiting. Have a nice day.

All is well

Regards: @meta007

Comments

[enforcer48]

Another geometric puzzle!

!discovery 37

[meta007]

Thanks man for you regular visit and appreciation though I am not regular😂

[stemsocial]

Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!

Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).

Thanks for including @stemsocial as a beneficiary, which gives you stronger support. 
 

[offia66]

You must be good in mathematics, I got to learn a few things reading through your article.

[meta007]

Hehe.. I don't if I am good or not but I love solving them. Thanks for visiting

[discovery-it]

This post was shared and voted inside the discord by the curators team of discovery-it
Join our Community and follow our Curation Trail
Discovery-it is also a Witness, vote for us here
Delegate to us for passive income. Check our 80% fee-back Program

---

[indiaunited]

This post has been manually curated by @bhattg from Indiaunited community. Join us on our Discord Server.

Do you know that you can earn a passive income by delegating to @indiaunited. We share more than 100 % of the curation rewards with the delegators in the form of IUC tokens. HP delegators and IUC token holders also get upto 20% additional vote weight.

Here are some handy links for delegations: 100HP, 250HP, 500HP, 1000HP.

_{100% of the rewards from this comment goes to the curator for their manual curation efforts. Please encourage the curator @bhattg by upvoting this comment and support the community by voting the posts made by @indiaunited.}

[intishar]

Your explanation was well as expected. I like the way how you describe everything..
!PIZZA

[meta007]

Thanks man for your visit and compliment.

[pizzabot]

PIZZA!

$PIZZA slices delivered:
@dayadam_(1/5) tipped @meta007
intishar tipped meta007

[coinjoe]

If I was a mathematics student, I would be all up in your posts. Defintely gonna keep you in mind for my youngest son when he starts college this next year though. I am sure he will have some difficult math with his major.

[meta007]

Definitely , If he fetches any problem, I can help him to solve it. In that case, feel free to hit a comment on any of my post. I'll be more than happy to help him out.

Thanks man for you sweet compliment and visit.
Have a good day.

[coinjoe]

That is very nice of you. Thank you.

[dayadam]

Excellent explanation for all those interested in mathematics, although I really studied a career that had nothing to do with it hahaha. I think my daughter would be interested in it. Thanks for sharing your knowledge @meta007 ✨

!PIZZA

[meta007]

No wory mam... Thanks for visiting. If she finds any unsolved problem, must pin me. I'll definately help her with a solution.

[sperosamuel15]

Great display... Thanks

[meta007]

Thanks man for your visit and compliment.

[sperosamuel15]

You're welcome

[hivebuzz]

Congratulations @meta007! You received a personal badge!

Happy Hive Birthday! You are on the Hive blockchain for 1 year!

_{You can view your badges on your board and compare yourself to others in the Ranking}