Hello maths bugs(🐞) and hivers(🐝)
Well come to another intesting concept with its proof. We know that the distance between Cir-cum-crntre and In-centre of a triangle is given by square root of (R²-2rR). Here R represents the Cir-cum-radius and r indicates In-radius of Cir-cum-circle and In-circle of a triangle. If you are not aware about these circle and radius, check In-circle and Cir-cum-circle alongwith their related things.
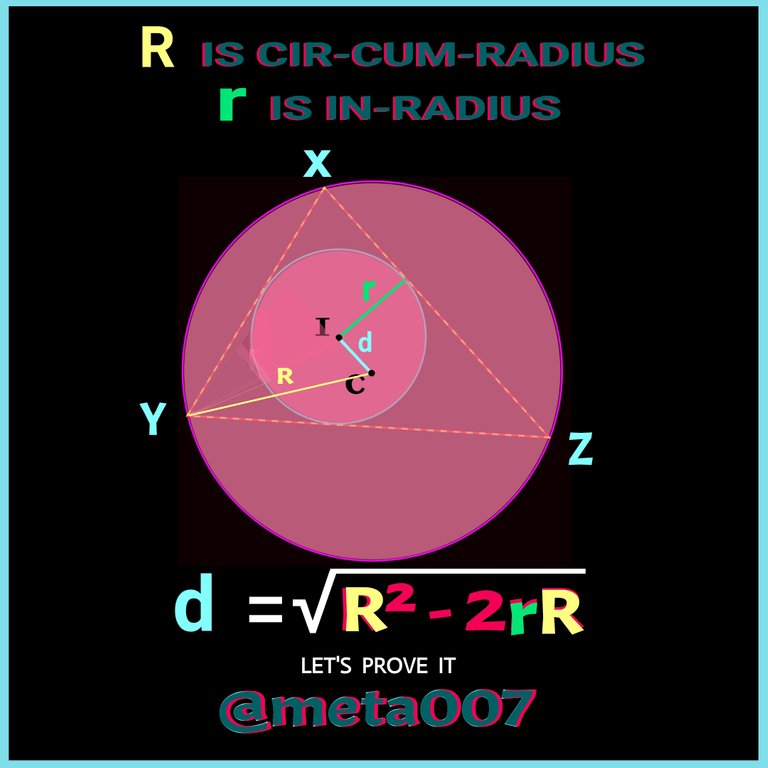
The proof today will be very complicted because of its numerous constructions at the same time. I'll try to darw all the construction calmly one in each figure for your better understanding and also I'll keep telling about each concept to help our proceeding. Let's begin..
Construction 1:
Let's produce IC to both way and conneted IX to down untill they meet outler line of the Cir-cum-circle. Here you must know when two chords of a circle meet inside the cirle, product of a liner segments always be equal to product of the other liner segments. That is IX×IL = IP×IQ. Check it 👇

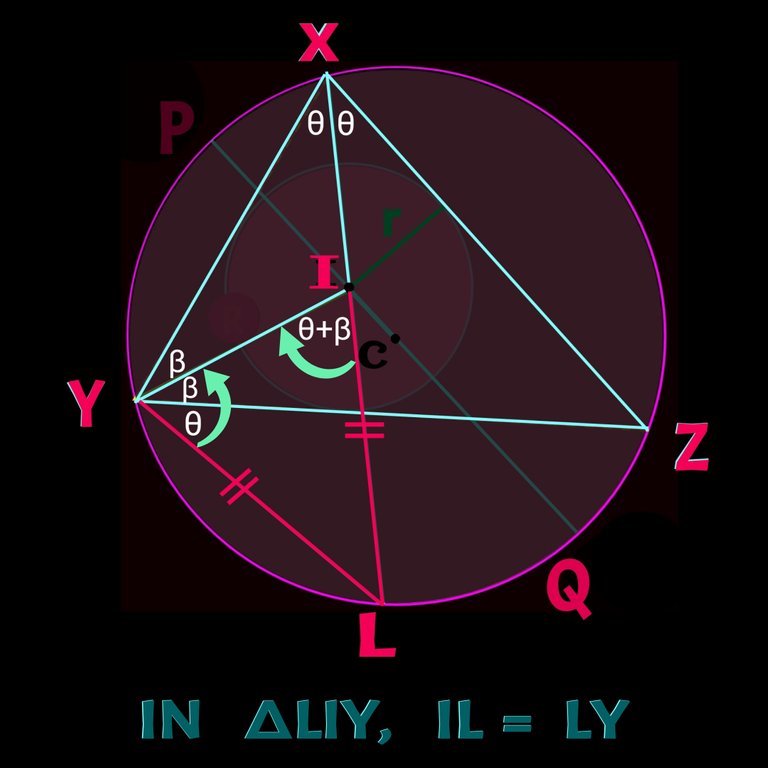
Construction 2 :
LY is connected. Now see, as I is in-centre, IX and IY are the bisectors of ∠YXZ and ∠XYZ Rrespectively. Now just consider ∆IYX and exterior ∠LIY. We know sum of opposite interior angles is equal to the exterior angle. So, ∠IXY +∠IYX = ∠LIY. Arc LQZ conceive two equal angle on the circumference. So ∠LXZ = ∠LYZ. As per the figure both are eaqual to θ.
Now, in ∆LIY, IL = LY. Check it 👇
Construction 3:
Let's connect LC and produce to M and now join MY. Let's also draw IN perpendicular to XY. IN = r. Here, LM going through Cir-cum-centre C is the Cir-cum-radius. So, LM = 2R.

Now, from ∆INX and ∆LMY in the above figure we have as follows:
∠INX = ∠LYX
And ∠IXN = ∠LXY
As two angle equal, third angle is also equal
So, ∆INX is similiar to ∆LYX
So , we can say IN/LY = IX/LM
Or, IN × LM = IX × LY
We have already proved that IL = LY in the figure of construction 2
So, we can say IN × LM =IX × IL
Now, If we repalce IX × IL in the equation IX × IL=IP×IQ what we have concluded in the figure construction 1 by IN × LM, we can have as follows:
IN × LM = IP × IQ
Let's take a final figure to draw the line:
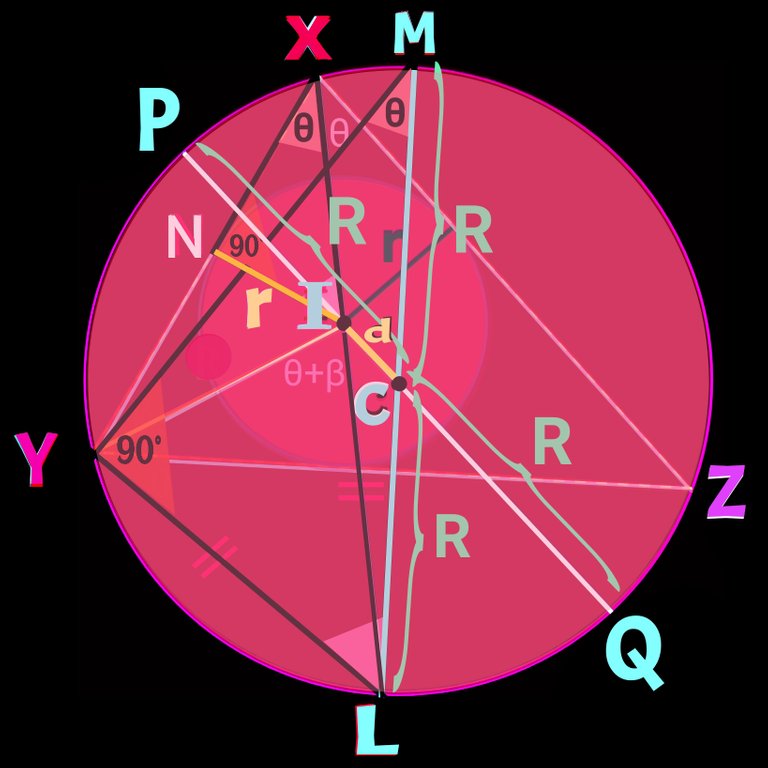
The above figure is conjested but nothing to do, we need all the staffs together now.
In the equation IN×LM=IP×IQ many things can be replace.
Check the figure IN = r
[ r* =In-radius of inner circle of∆XYZ]
And LM = R+R= 2R
[R = Cir-cum-radius of outer circle of ∆XYZ
Again, IP= (R - d) and IQ = (R + d)
So, Replacing all of them we can conclude
r × 2R = (R - d) × (R - d)
Or, 2rR = R² - d²
Or, d² = R² - 2rR
Or, d = √(R² - 2rR) [ proved ]
It's a very important conclusion; suppose if you are asked to find distance between cir-cum-centre and in-centre of a triangle and you are given cir-cum-radius and in-radius only.
Let's me ask you to solve a problem:
Here you go, if 2R = 5 cm and r = 1 cm , Find the distance between two centres.
Thanks you so much guys staying till end.
I hope you like the the explanation. From my part or for you, if anything is missing, please feel free to ask for.
All the figures are made by me using android app. and here may be some silly mistakes; please try ignoring it if you can. Re-editing hurts.
Have a nice day
All is well
Regards: @meta007
Totally did not remember this from geometry class.
!discovery 41
I did not encounter it in geometry class of school life. Later I found it in book in advance section.
Thanks man for your always visit and support.
Have a good day.
hehe. Coincidently last day my students were doing almost kinds of geometry but not the exact one you shared here.
!PIZZA
Really! Good to know that. Hehe
Thanks man for visiting.
Have a nice day.
Yay! 🤗
Your content has been boosted with Ecency Points
Use Ecency daily to boost your growth on platform!
Support Ecency
Vote for new Proposal
Delegate HP and earn more, by @meta007.
Discord Server.This post has been manually curated by @bhattg from Indiaunited community. Join us on our
Do you know that you can earn a passive income by delegating to @indiaunited. We share more than 100 % of the curation rewards with the delegators in the form of IUC tokens. HP delegators and IUC token holders also get upto 20% additional vote weight.
Here are some handy links for delegations: 100HP, 250HP, 500HP, 1000HP.
100% of the rewards from this comment goes to the curator for their manual curation efforts. Please encourage the curator @bhattg by upvoting this comment and support the community by voting the posts made by @indiaunited.
$PIZZA slices delivered:
(1/5) @intishar tipped @meta007
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
Thanks for including @stemsocial as a beneficiary, which gives you stronger support.