Helo math bugs(🐞) and hivers(🐝)
Well come to another intersting gemetric concept. Here I am going talk about Ex. Here Ex means Exo or outer and thus ex-centre become outer centre of a triangle.
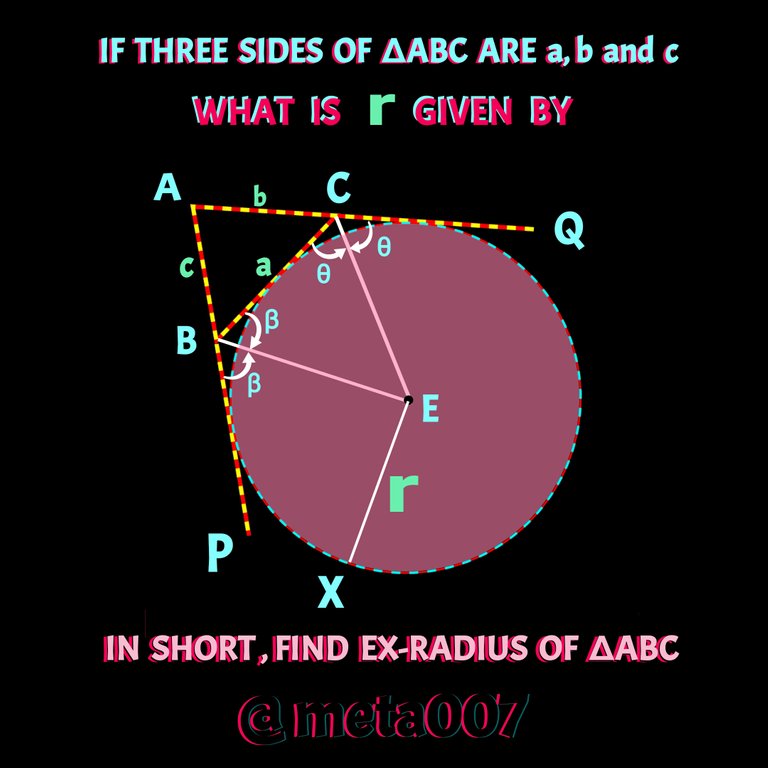
The three sides of ∆ABC are AB, BC and AC. Here in the following picture the O centric circle touches the three sides of ∆ABC. The radius of the circle is called ex-radius. We need two know that the external bisectors of angle B and C will meet at the ex-centre.
There will three ex-centres and three radius.We will just prove one of them and other two can be proved the same say. We are going to prove the ex-radius on not extended side BC and we call it simply r.
We need a simple construction also; let's connect Vertex A and ex-centre E. Check the following figure also.let's also draw the height of ∆ABE and ∆ACE. Each case the height will be r.

Note: For a triangle the height is always perpendicular distance between a vertex and it's opposite side. Hence, a height of a triangle can be outside of the triangle. Here r is the height as a radius is always perpendicular to the point of contact of a tangent.
Let's now concentrate how we can find the area of ∆ABC taking the known variables a,b,c and r. Area of ∆ABE can be given by cr/2 unit² and that of ∆ACE be br/2 and for ∆BEC it will be ar/2. Let's check them below: 👇
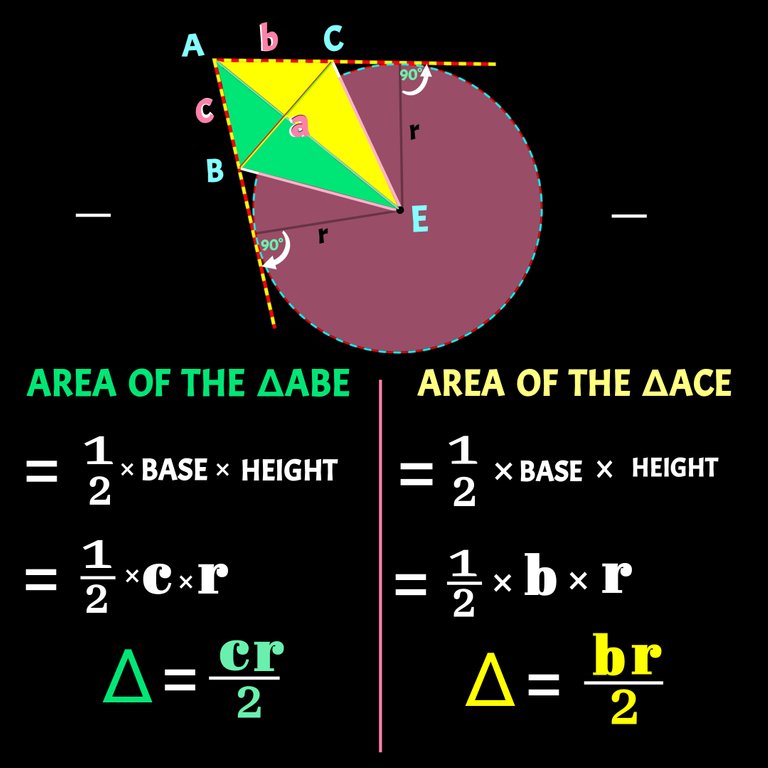
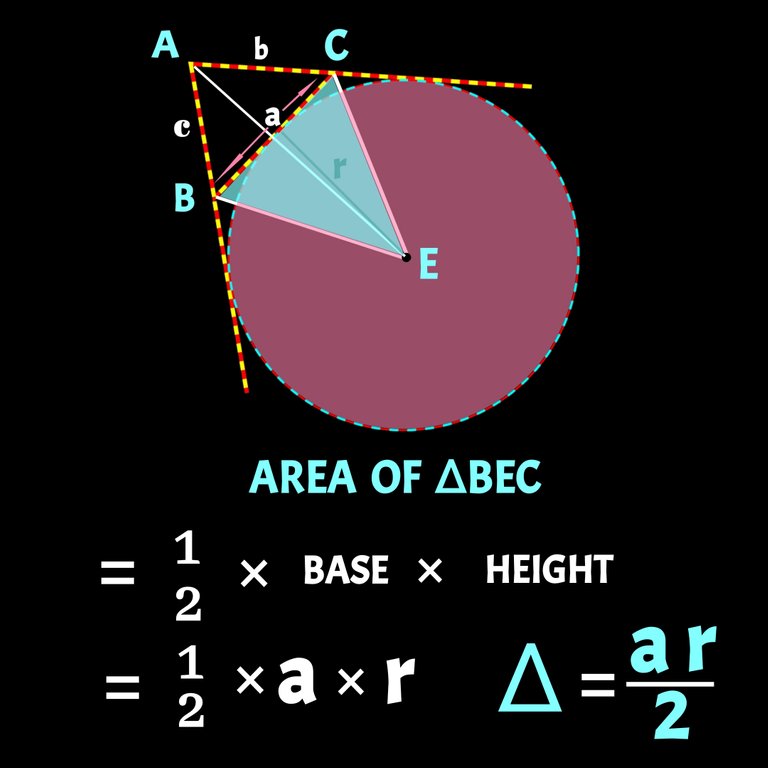
Now we can find the area of ∆ABC.
So, ar.∆ABC = ar. ∆ABE + ar. ∆ACE - ar. ∆BEC. Check it below: 👇


Now time for further calculation. We can write the radius of ex-centre in the form r= ∆/(s-a). Lets check it below: 👇
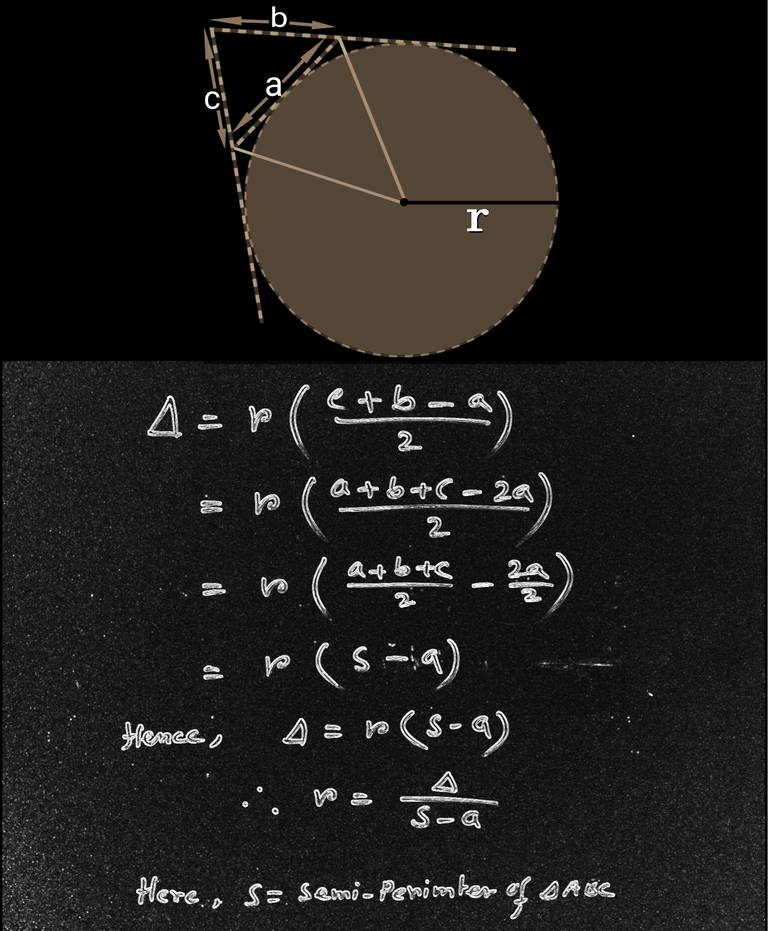
There will three ex-circles and their ex-radius can be given by
r' = ∆/(s-a) unit²
(Radius is perpendicular to not extended side a)
r'' = ∆/(s-b) unit²
(Rdaius is perpendicular to not extended side b)
r''' = ∆/(s-c) unit²
(Radius is perpendicular to not extended side c)
These formullae of radius is very similar to the general one which is given by r = ∆/s , Here r = inradius not the ex one. You can check it here.
🎤🎤All the figures used here is made by me using android application. If you find any silly mistake(s), try ignoring it and just consider the data as the figure may not be accurate in measurement.
Thanks you so much for visiting.
I hope you find my post interesting and effortful.
Have a good day.
All is well
Regards: @meta007
Heheh, once again making mathematics look like it's CRS that's very easy😂
CRS..haha lol
Thanks man for visiting.
Have a good day.
You're welcome
It is very effortful! Math is great science dude. congratulations for the post
Thank you so much for your visit and compliment. It means a lot.
🤗🤗🤗
Congratulations your publication has been chosen among the best of the day.
KEEP CREATING GOOD CONTENT.
Thank you so much for the appreciation. It means a lot.
Discord Server.This post has been manually curated by @bhattg from Indiaunited community. Join us on our
Do you know that you can earn a passive income by delegating to @indiaunited. We share more than 100 % of the curation rewards with the delegators in the form of IUC tokens. HP delegators and IUC token holders also get upto 20% additional vote weight.
Here are some handy links for delegations: 100HP, 250HP, 500HP, 1000HP.
100% of the rewards from this comment goes to the curator for their manual curation efforts. Please encourage the curator @bhattg by upvoting this comment and support the community by voting the posts made by @indiaunited.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
Thanks for including @stemsocial as a beneficiary, which gives you stronger support.