
In this opportunity we will relate to some algebraic expressions called trigonometric ratios, but also with another formulation that serves us for the volumetric calculation of a certain pond, therefore, in addition to the calculation of the volume, we will calculate the internal angles of a ladder placed on the pond for water to be analyzed.
On many occasions our students ask themselves the following question:
Is it possible to apply the algebraic formulations seen in class in our daily life?
It is one of the most common questions that we are going to answer, and it is just one example of countless others that we can carry out in each of our daily activities, so let's proceed to the following example.
exercise
A family has in their house a rectangular water tank (pool type) whose measures are height: 111 cm (1.11 meters), length: 404 cm (4.04 meters) and width: 224 cm (2.24 meters), also to enter the water tank there are two stairs, one of them on the outside and the other on the inside, then the images are shown where you can see the characteristics described above in the following figure 1:


In relation to the approach described above, answer to the following questions:
a.- What will be the volume of water in liters and gallons needed to fill this water tank?
b.- What are the internal angles of the external ladder supported by the tank?
Solution
Data:
h = 111 cm o 1,11 m (Tank height).
L = 404 cm o 4,04 m (Tank length).
A = 224 cm o 2,24 m (Tank width).
V = ? (Volume of water required).
Internal angles of each staircase?
To begin to answer the first question, let's look at the first formula:
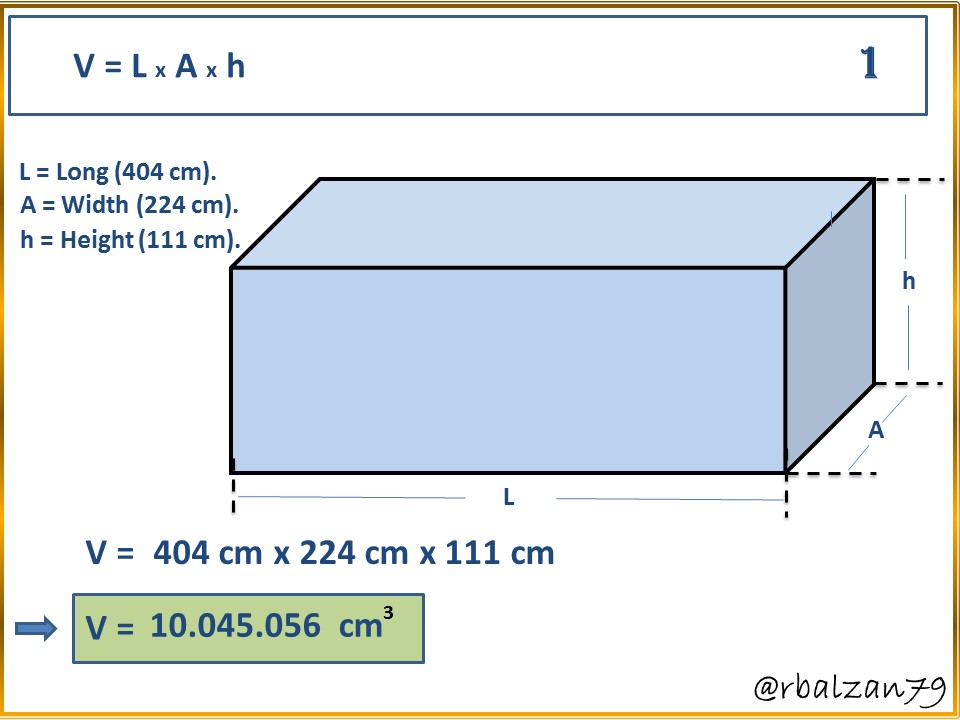
With formula 1, we were able to determine the required volume of water, but, in cubic centimeters, we must now take it to the required units, i.e., liters (L) and gallons (gal), therefore, we have the following:

In this way they could notice how the resultant volume in liters was 10,045.05 liters and if we want it in gallons, it would be 2,653.62 gallons.
b.- To answer the second question it is important to know some trigonometric ratios for the determination of angles of right triangles, and as we could notice in the previous images, the staircase to be analyzed forms a right triangle with the wall where the staircase is supported.
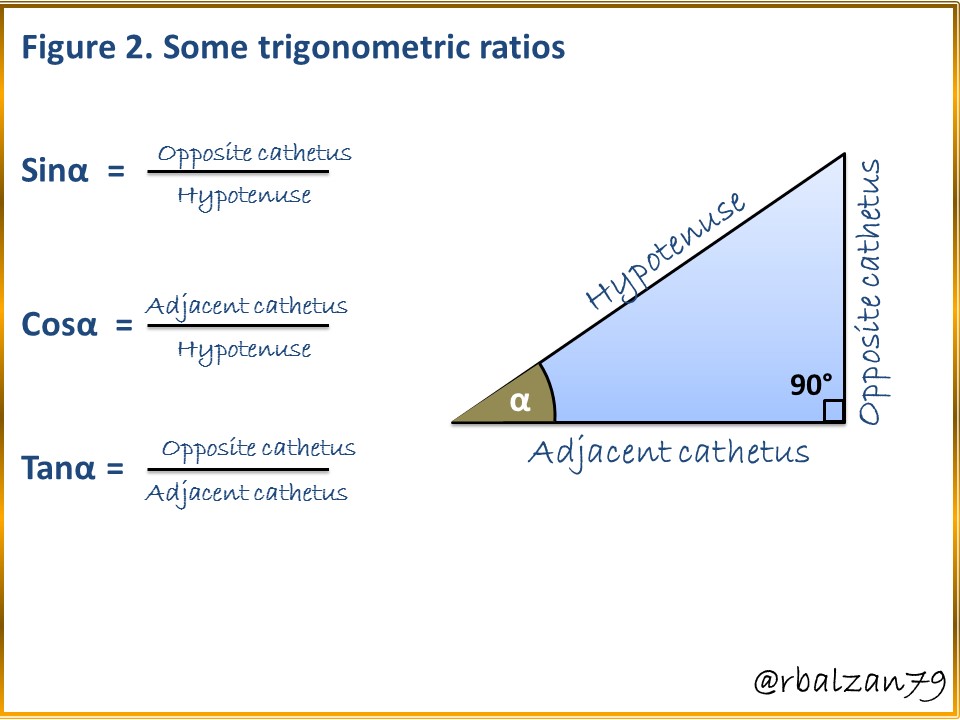
Once we have observed some trigonometric ratios such as sine, cosine and tangent, with a tape measure we proceed to measure each of the sides of the right triangle formed by the ladder located on the outside of the pond as shown in the following figure 3 and 4.


Each of the sides are measurable, therefore, we can know the value of each side of the right triangle indicated, then, this leads us to express that it is possible to use any of the trigonometric ratios mentioned above, in this case, I will use the tangent ratio since those were the sides which I proceeded to measure, i.e., the length of each of the legs.

Thus we know a second angle (α = 59.53°), now we only have to find the third angle and, for this we know that the sum of the internal angles must give us 180°, therefore, we proceed as follows, we will call β the right angle (90°) and θ the remaining angle, then, we have:
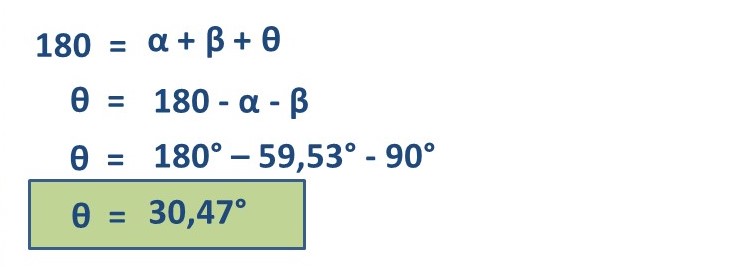
Now we have the value of the three component angles of the right triangle originating from the ladder resting on one of the sides of the pond, observed in Figure 3, therefore, α = 59.53°, β = 90° and θ = 30.47°, the sum of these three angles results in 180°.
Conclusion
Everything that surrounds us constantly tells us that we can know more about them if we wish, the mathematical formulations are extracted from long processes of experimentation of each event or occurrence that takes place next to us, then these formulations are spread everywhere, especially to those educational spaces in order to explain them and make them known in depth.
Many times people are unaware of the immense usefulness of each structured algebraic formulation, especially our students, it is important to make them understand that these formulations are not only explained to solve problems in class, they are also extremely useful outside the classroom, the whole field of science is nourished by them, and it has been through them that we have developed to the maximum, this time I only showed a small but valuable example of application of these mathematical formulations in our daily life, I hope to continue with this purpose later on.
Until another opportunity my dear friends.
Note: The images are property of the author and edited using Power Point and Paint, the animated gif was originated with PhotoScape.
Recommended Bibliographic References
[1] Volume of Rectangular Prisms. Link.
[2] Trigonometry. Link.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.
Thank you for your valuable support dear community. Regards.