Movimiento en línea recta por tramos.
Continuando con la solución de problemas en una dimensión, en este artículo presento cinco videos donde explico las soluciones de problemas interesantes. En este caso el movil se mueve con características diferentes en varios tramos del desplazamieto.
He escogido, como siempre, los problemas que más son consultados por los estudiantes de Física 1. Previo a los videos hago un resumen de las ecuaciones y fórmulas que se necesitan para resolver los problemas que se plantean en cada uno.
Movimiento en una dimensión con aceleración constante



Video 1. Uso de las derivadas e integrales, propiedades del logaritmo y artificios matemáticos.
Video 2. Movimiento rectilíneo por tramos, uso de fórmulas y construcción de gráficas
Video 3. Movimiento por tramos, uso de fórmulas.
Video 4. Movimiento por tramos. Demostración usando fórmulas y uso de la matemática.
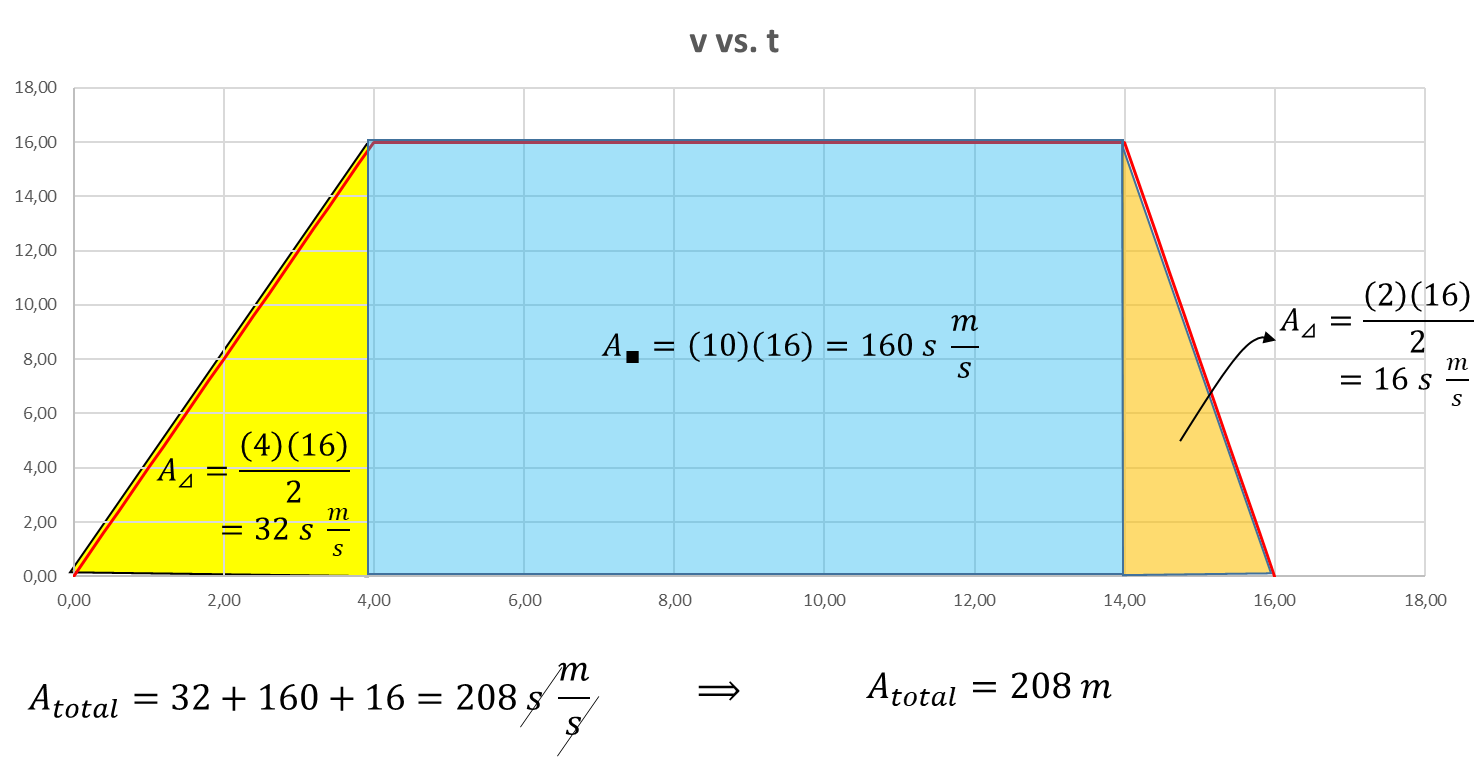
Video 5. Movimiento por tramos, construcción de gráficas y uso de la geometría.
Bibliografía
- Finn E. J., Alonso M. Física Vol I: Mecánica. Fondo Educativo Interamericano, México, 1971.
- Sears F. Zemansky, Young H., Freeman R. Física universitaria, 11ra. Ed., Volumen I, Pearson Addison Wesley, México, 2004.
- Feynman R., Leighton R. Física Volumen I. Mecánica, radiación y calor. Addison-Wesley Iberoamericana, Argentina, 1987.
- Arons A. Evolución de los conceptos de física. Trillas, México, 1970.
- Hewitt P. Física conceptual. Pearson Addison-Wesley, México, 2007.
- French A. P. Mecánica newtoniana. MIT Physics Courses. Reverté, Barcelona, 2006.
- Resnick R., Halliday D. Física Volumen 1. Compañía Editorial Continental. México, 2001.
- Landau L. D., Lifshitz E. M., Mecánica Vol. 1. 2da. Ed, Reverté, Barcelona, 1965.
- Kittel C., Kight W. Mecánica. Berkeley Courses Vol. 1., Reverté, Barcelona, 1989.
Fuentes de las imágenes
Todas las imagenes fueron hechas por mi mediante la utilización del software Power Point (PPT).


Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.
Congratulations @rnunez09! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s):
Your next target is to reach 55000 upvotes.
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPCheck out the last post from @hivebuzz:
Support the HiveBuzz project. Vote for our proposal!
Hola amigo @rnunez09. Este es lo bonito de la física y la matemática, para este caso de cinemática que estás tratando, se ve a leguas por el gráfico, que si analizamos el movimiento desde el punto de partida hasta el punto final se denota que es movimiento rectilíneo pero con cambios de ritmo, por lo que se hace muy propicio para calcular su velocidad y aceleración ser analizado por tramos.
La geometría ayuda mucho, claramente el primer tramos lo podemos realizando el cálculo de la pendiente de la recta, y en el caso de calcular el área bajo la línea recta lo podemos hacer calculando el área del triángulo o inclusive con la aplicación de integrales para el cálculo del área. En el segundo tramo no existe cambios de la velocidad (movimiento constante) por lo que la aceleración es nula y la velocidad constante, el área es la de un rectángulo.
Para el tercer tramo se ve que la velocidad empieza a caer de forma lineal, por lo que dicha desaceleración se puede calcular calculando su pendiente, mientras que su área se puede calcular de forma geométrica o mediante la aplicación del cálculo integral.
Ese primer gráfico habla por sí solo, las demostraciones aquí hechas le dan un valor excepcional porque de esa manera podemos ver las distintas variables y formas que tenemos para atacar la solución de los cálculos de velocidades, distancias, aceleraciones, siempre teniendo en cuenta el aporte del cálculo diferencial e integral, la geometría y álgebra.
Saludos maestro, estaré al tanto de nuevas publicaciones las cuales me estimulan mucho para desarrollar la creatividad en esta área.
Muchísimas Gracias, carlos84.
Aprecio mucho tu comentario y tus aportaciones que mejoran sin duda mi publicación y me motivan a seguir haciendolas. Una vez más muchísimas gracias y disculpa lo tarde de mi parte en responder a tan importante comentario.