LINEAR MODELS AND THEIR APPLICATIONS IN ECONOMICS

[analealsuarez]

Is a powerful tool that allows us to model in an abbreviated way, problematic situations of reality in order to give us the facility to solve a problem in the context where we operate, it is enough to identify clearly and precisely which are the variables involved in it, and differentiate which of them depends on the other variable, that is, we must identify the independent variable and the dependent variable.

---

In the particular case of problems in the context of Economics, the variables with which we are going to get, have to be those linked to the world of economic sciences, such as: Cost, Income, Profit or Profit, Supply and Demand, among others.

---

The case at hand, and since the theory on functions and their respective domains is already known, we want to introduce these economic models in the context of linear functions.

---

I recommend reading, beforehand, the following post: FUNCIONES E IDENTIFICACIÓN DE VARIABLES EN EL CONTEXTO DE LA ECONOMÍA///FUNCTIONS AND IDENTIFICATION OF VARIABLES IN THE CONTEXT OF THE ECONOMY

---

Let us begin by first defining each of these functions:

---

Total Cost function: C(x)= F.C. + V.C.

---

Total Cost function C(x) summarizes the expenses that an entrepreneur must incur to produce x quantity of his goods.

---

Is a difference in these costs, and that is that there is a permanent cost that involves fixed payments made by the entrepreneur to maintain the conditions of its production, such costs are, for example: rent of the premises, payment of services, insurance, etc., this type of cost is called Fixed Cost F.C.. in short, the fixed cost does not depend on production.

---

Variable Cost V.C. if it depends on the quantity x of merchandise produced, because here are summarized the expenses that involve: raw material, labor and other additional expenses that the entrepreneur may eventually require to produce quantity x of his merchandise.

---

In general terms, the Total Cost is the monetary amount invested by the entrepreneur to produce x amount of goods, and corresponds to the total costs, that is, the sum of the Fixed Cost (.F.C) plus the Variable Cost (V.C.).

---

Total Income Function: I(x)=px

---

entrepreneur produces his quantity x of merchandise with the purpose of selling it to obtain profits and in this sense, he places a price ''p'' per unit to his product, in this way, the income perceived by the sale of this merchandise, is determined by the product of the price p by the quantity x of merchandise sold, that is to say: p.x. When the entrepreneur sells x quantity of merchandise, he receives a Total Income I(x)=p.x; which, in general terms, is the monetary quantity that the entrepreneur receives for selling x units of merchandise, at price p.

---

Gain function: G(x)=I(x)-C(x)

---

objective of the entrepreneur is to obtain profits with his enterprise, in this sense, he must be clear about how much he wants to earn, within the rationality of the market, for the production and sale of his product, for this, in his calculations must prevail the idea that the total income must exceed the costs in order to obtain profits, that is: I(x)> C(x), since if I(x)= C(x), the entrepreneur will have losses: I(x)= C(x) the entrepreneur recovers the costs and if I(x)< C(x), the entrepreneur will have losses.

---

Equilibrium point.

---

When I(x)= C(x), i.e., when the entrepreneur recovers the costs, it is said that he has reached the Break-even Point.

---

For now, let's deal with these three models and start with some examples, here we have the following problem:

---

The fixed costs to manufacture a certain item are $300 per week and the total costs to manufacture 20 units are $410. Determine the relationship between the total cost and the number of units produced, assuming it is linear. What will be the cost to manufacture 30 units per week?

---

Solution:

Let us first identify the variables:
x: is the quantity of items produced.
y=C(x): represents the total cost of producing x number of items.
It is known from the problem data that F.C.= 300 and the variable cost of producing 20 items is V.C.= 410.

---

And it is also known that the cost model is linear, therefore, let's represent it in the coordinate axis system in order to get a graphical idea of the problem and understand it better.

---

Let's plot the coordinate axis system, the abscissa axis will represent the quantity x of goods produced, and the y-axis will represent the cost of producing that quantity x of goods.

---

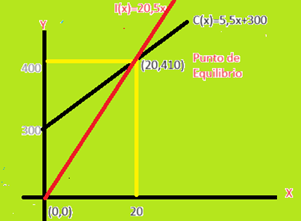
In these problems we preponderate the positive semi-axis of the x, since logically in these problems it is about production and sale of products, it does not make sense to consider negative values for the x.

---

When we talk about Fixed Cost C.F. we mean that this is a permanent cost even when there is no production, a factory can be active a certain time and not be producing, and in such sense its production x is 0, but its monthly fixed costs, in this case, is 300. Therefore, the point of coordinate x=0 and abscissa y=300 must go on the graph, we will call it A= (0,300).

---

Says the problem that the production of x=20 items have a fixed cost of y=410; then point B= (20, 410) must also be located on the plane.

---

---

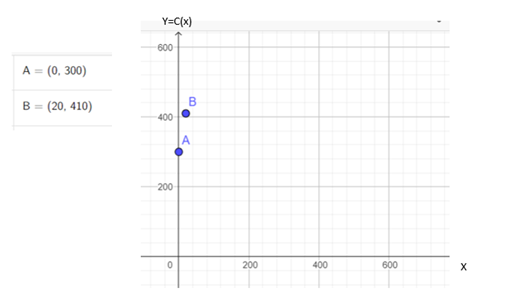
We know that the cost model is linear, so we will draw a ray starting at point A and passing through B.

---

Like this:

---

---

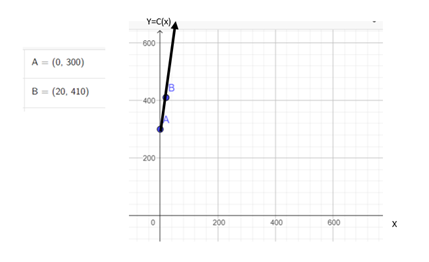
We see in the graph the description of the problem, in it we observe that as x grows (production increases) y also grows (production costs increase), obviously it is an increasing straight line.

---

algebraic description of this model is missing, i.e. the equation describing this line, for this purpose, we will use the equation Slope Intersection at the Origin: y=mx+b, which in our case is C(x)=mx+b.

---

According to the graph b=300, therefore, our cost function, so far, is C(x)=mx+300. It remains to obtain the value of the slope m.

---

Recall the slope formula, given two points P and Q through which a line passes, then the slope formula is given by:

---

---

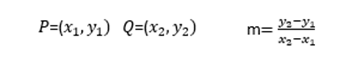
In the problem we have been developing, we have two points: A= (0,300) and B= (20,410), applying the slope formula:

---

---

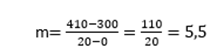
Finally, our functional cost model is: C(x)=5.5x+300.
If we want to determine the cost of manufacturing 30 items, we substitute x=30 and calculate C(30)=5.5.30 +300=165+300=465.

---

That is, the cost of producing 30 items is $465.

---

If the manufacturer decides to sell his product at a price p=20.5, what is the model that defines the total revenue function?

---

Recall that I(x)=px, in this case, we substitute p=20.5 in that model, resulting that: I(x)=20.5x

---

Let us validate our model by substituting x=20, thus: I(20)=20.5.20=410, which is congruent with the stated problem.

---

And in this case, what is the profit model G(x) ?
G(x)= I(x)-C(x)

---

Substituting the above Revenue and Cost models, we get:
G(x)=20,5x-(5,5x+300)

---

We eliminate the parenthesis:
G(x)=20.5x-5.5x-300.

---

Then, our gain model is:
G(x)=15x - 300

---

With this model, we can determine the number of units that must be produced and sold at a price p (in this case 20.5) in order for the entrepreneur to make a profit.

---

For example, if the producer manufactures and sells 20 items, what will be his profit?

---

To answer this question, we must calculate G(20)=15.20-300=300-300=0.

---

This tells the producer that producing and selling 20 items at the price 20, 5 pains, does not yield him profit, thereby only recovering costs. But, in this case we have reached the Break-even Point, this point is where revenue and cost are equalized. That is, break-even point is (20,410).

---

If we want to see this on the graph we must locate two points where the revenue line passes through, one of them is (20, 410) and the other is (0,0) since the revenue of 0 is I(0)=20,5.0=0.

---

Let us see:

For the producer to gain it must be satisfied that G(x)>0, that is:
15x - 300>0

---

Solving the inequality, we are left with:
15x >300
x >300/15
x >20

---

That is, the producer must produce and sell 21 items or more in order to make a profit.

---

In the event that he produces and sells less than 20 items he will make a loss.

---

This happens when 15x - 300<0

---

The following graph summarizes the results:

---

---

Credits:

The post is entirely original to the author.
The graphics were made with the support of Geogrbra and Paint.
Click here to see the article in Spanish
https://hive.blog/spanish/@analealsuarez/linear-models-and-their-applications-in-economics

Comments

[hivebuzz]

Congratulations @analealsuarez! You received a personal badge!

Happy Hive Birthday! You are on the Hive blockchain for 7 years!

_{You can view your badges on your board and compare yourself to others in the Ranking}

Check out our last posts:

Hive Power Up Day - July 1st 2024

[ekojah]

Nice work.