.png)
Ora che siamo a conoscenza del funzionamento base di Matlab e siamo in grado di gestire i dati e la programmazione di primo livello, possiamo affrontare più nel dettaglio la gestione dei vettori e le operazioni su di essi.
I vettori e le matrici compongono il cuore di Matlab ed il software è interamente sviluppato sulla gestione e l'analisi di questi.
Anche gli scalari sono matrici 1x1!!
Differenti Variabili Numeriche
MATRICI: i valori sono memorizzati in m righe e n colonne (m-by-n).
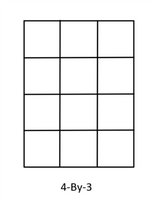 Per esempio --> v =[ 1 2 3; 4 5 6; 7 8 9; 10 11 12]
Per esempio --> v =[ 1 2 3; 4 5 6; 7 8 9; 10 11 12]VETTORI RIGA: i valori sono memorizzati in 1 riga e n colonne (1-by-n).
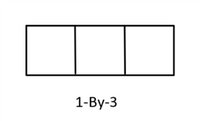 Per esempio --> v =[1 2 3] o v =[1:3]
Per esempio --> v =[1 2 3] o v =[1:3]VETTORI COLONNA: i valori sono memorizzati in m righe e 1 colonna (m-by-1).
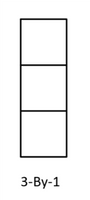 Per esempio --> v =[1; 2; 3]
Per esempio --> v =[1; 2; 3]SCALARE: un singolo valore è memorizzato in una cella 1x1 (1-by-1).
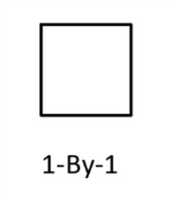 Per esempio --> v =1 o v =[1]
Per esempio --> v =1 o v =[1]
Come possiamo notare dagli esempi nella dichiarazione dei vettori o delle matrici il punto e virgola funge da divisore delle righe e lo spazio delle colonne.
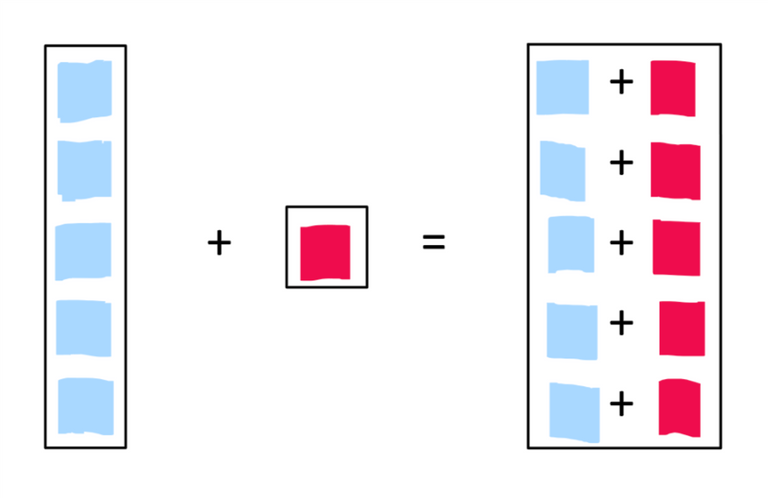
Espansione scalare
| Operatore | Simbolo |
|---|---|
| Addizione | + |
| Sottrazione | - |
| Moltiplicazione | * |
| Divisione | / |
| Esponente | ^ |
In questo caso invece stiamo aggiungendo/togliendo/moltiplicando/dividendo un elemento scalare ad un vettore. Ogni elemento di quest'ultimo sarà modificato, a seconda dell'operatore utilizzato, dallo scalare stesso.
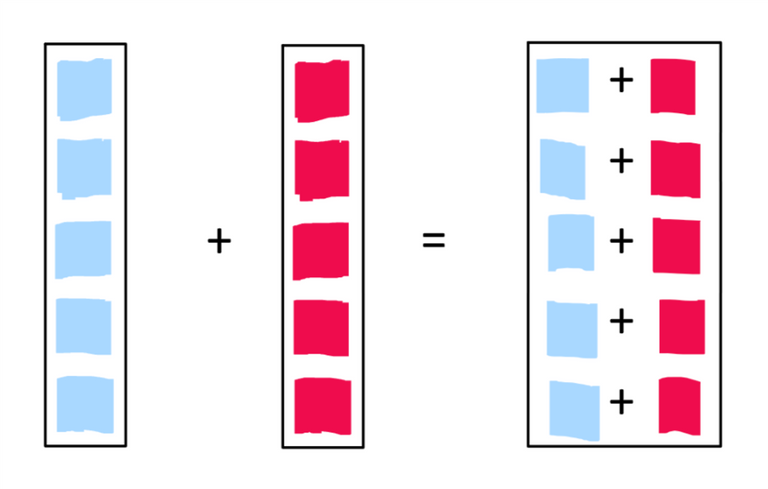
Operazioni Aritmetiche
| Operatore | Simbolo |
|---|---|
| Addizione | + |
| Sottrazione | - |
| Moltiplicazione Puntuale | .* |
| Divisione Puntuale | ./ |
| Esponente Puntuale | .^ |
In questo modo, per esempio, stiamo andando a moltiplicare il primo elemento del primo vettore con il primo elemento del secondo vettore, il secondo con il secondo e così via.
Per questo motivo i due vettori devono assolutamente avere le stesse dimensioni, altrimenti andremo incontro ad un messaggio di errore.
Operazioni e Funzioni sui vettori
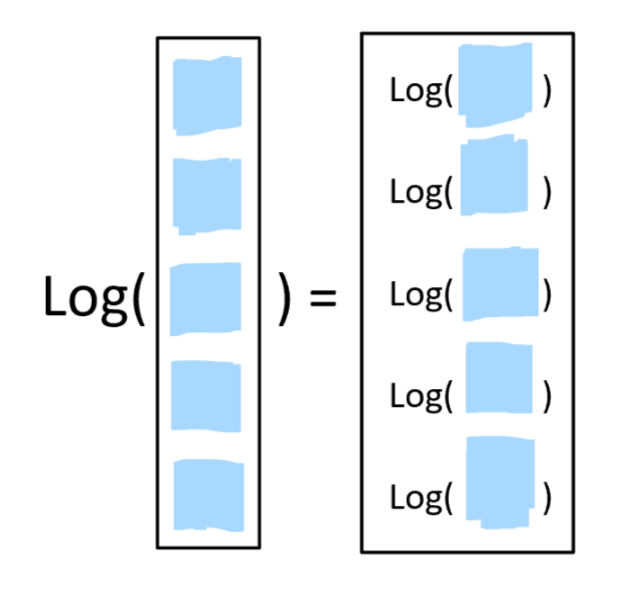
Analogamente alle operazioni aritmetiche, alcune funzioni sono "vettorializzate".
Questo permette di utilizzare un singolo comando per modificare allo stesso modo tutti gli elementi di un vettore.
Questo strumento, seppur banale, ha delle potenzialità enormi e facilita di molto l'utilizzo vettoriale/matriciale delle variabili.
| Funzione | Simbolo |
|---|---|
| Seno | sin |
| Coseno | cos |
| Logaritmo | log |
| Arrotondamento | round |
| Modulo | mod |
| Radice quadrata | sqrt |
Calcolo Statistico con i vettori
All'interno di Matlab è inoltre possibile interrogare i vettori per riuscire a carpire alcuni dati rilevanti senza dover analizzare ogni singolo elemento.
Ad esempio, alcune funzioni come max e min, sono in grado di estrarre il valore massimo o minimo all'interno di un vettore.
Dobbiamo porre molta attenzione nel caso in cui anche solo uno dei vettori di dati soggetti al calcolo presentasse un valore NaN ("Not a Number") dovuto a un qualche errore o ad un dato mancante.
Questo comporterebbe l'assunzione del valore NaN anche come uscita delle funzioni utilizzate facendoci perdere dati.
Per ovviare a questo problema basterà inserire alla funzione 'omitNaN' come secondo input:
>> ValoreMedio = mean(VettoreInput, 'omitNaN')
Alcune funzioni utili e il loro funzionamento:
| Funzione | Risultato |
|---|---|
| max | Ritorna il valore massimo |
| min | Ritorna il valore minimo |
| mean | Ritorna la media degli elementi |
| median | Ritorna la mediana degli elementi |
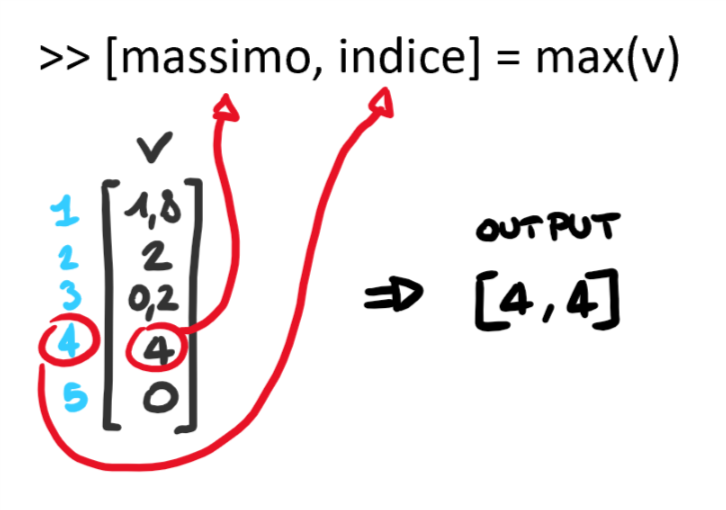
Possiamo notare come le funzioni max e min possono essere usate, come da immagine, per ottenere l'indice di posizionamento del valore. Risulta molto comodo quando l'indice del valore cercato di v è correlato al valore presente sullo stesso indice di un altro vettore (per esempio con i vettori MarketCap e Date dell'esercitazione precedente).
Indicizzazione nei vettori
Ma una volta scoperto che il valore massimo di capitalizzazione di mercato di Bitcoin ha un indice 8, come possiamo trovare il giorno in cui il prezzo era massimo?
Come si può utilizzare l'indice di posizione scoperto per estrarre il giorno corrispondente dal vettore Date?
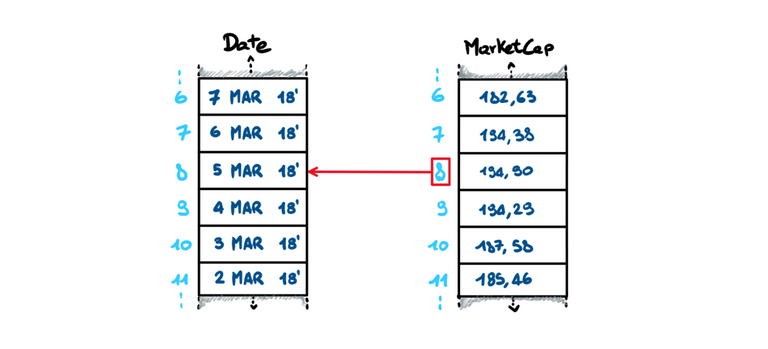
Ogni elemento di ogni vettore ha un indice e in Matlab l'indice del primo elemento è 1.
Possiamo quindi avere accesso ad un dato di un vettore specificandone l'indice tra parentesi dopo il nome della variabile:
>> MaxMarketCap = MarketCap (8)
Questo comando assegna il valore massimo di capitalizzazione in miliardi di dollari, allocato in indice 8, alla variabile MaxMarketCap e visualizza nella Command Window.
Invece di utilizzare un numero si potrebbe utilizzare una variabile come indice.
In questo modo potremmo far dipendere questa variabile da altri parametri all'interno del codice, creare delle dipendenze e correlazioni o selezionare solo sotto-sequenze inserendo indici vettoriali che andranno ad estrarre solo parte dei valori del vettore intero.
Si può utilizzare la parola chiave end come indice per puntare all'ultimo elemento di un vettore indipendentemente dalla sua lunghezza.
Assegnando invece un valore ad un indice non esistente, il software in automatico aggiungerà tanti zeri pari a quelli che mancano per arrivare all'indice di inserimento. Più facile a farsi che a dirsi:
>> x = [1 2 3];
x(6)=33
x =
1 2 3 0 0 33
Alcuni operatori 'comodi'
TRASPORRE UN VETTORE: grazie all'operatore ' siamo in grado di trasporre i vettori. Può essere utilizzato per trasporre anche vettori con numeri complessi trasformandoli (') o meno (.') in complessi coniugati.
>> v = [1 2 3]; >> q = v' q = 1 2 3OPERATORE COLONNA: grazie all'operatore : siamo in grado di decidere quali saranno i valori iniziali, i valori finali e la spaziatura tra ogni elemento di un vettore. Se viene omesso dx il software prende di default il valore 1 di spaziatura.
>> x = v1:dx:v2
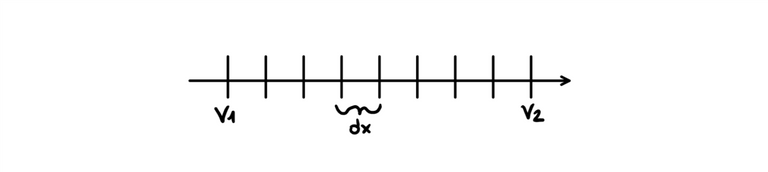
OPERATORE LINSPACE: grazie a questo operatore siamo in grado di decidere quali saranno i valori iniziali, i valori finali e il numero di elementi che intercorreranno tra i due. Se vengono omessi gli elementi di ingresso per l'operatore, esso crea di default un vettore di 100 elementi.
>> x = linspace(v1,v2,n)
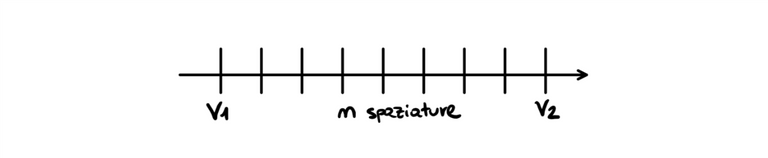
Possiamo notare inoltre come tutti questi siano definiti come vettori riga. Quanto appreso ci permette di trasporre questi vettori nel caso in cui volessimo renderli vettori colonna.
Analisi tipologie di grafici vettoriali
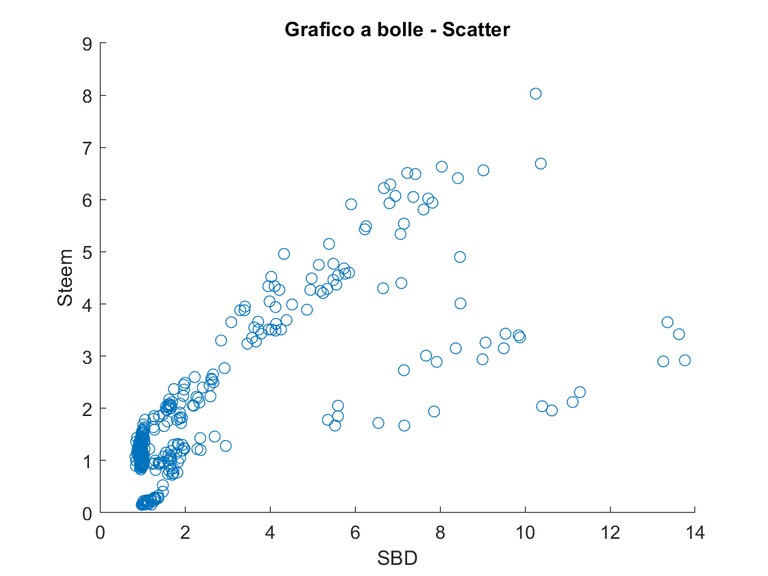
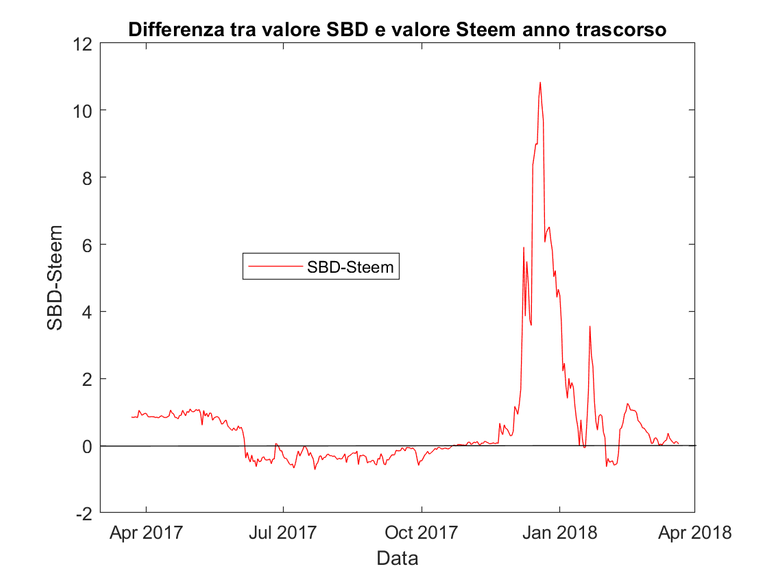
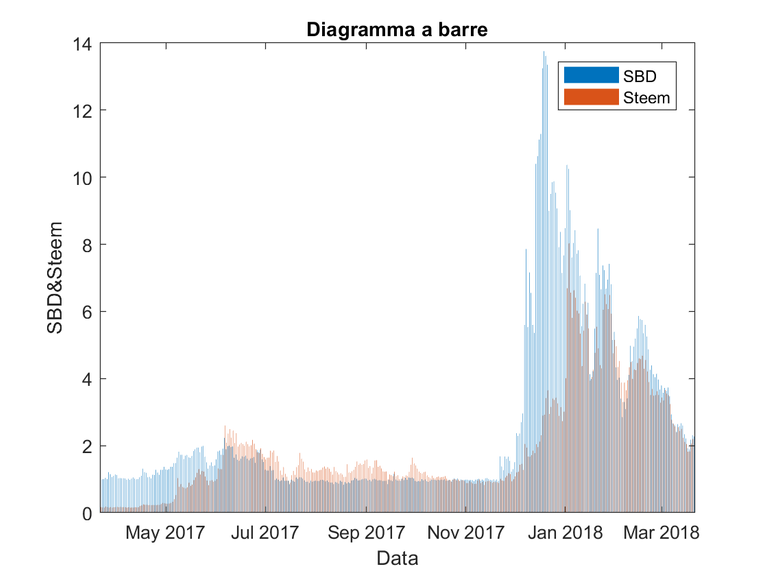
| Funzione | Descrizione |
|---|---|
| scatter | Grafico a bolle, con dimensioni e colore variabili dell'indicatore |
| bar | Grafico a barre (verticali e orizzontali) |
| stem | Grafici a sequenze discrete |
| stairs | Grafici a scale |
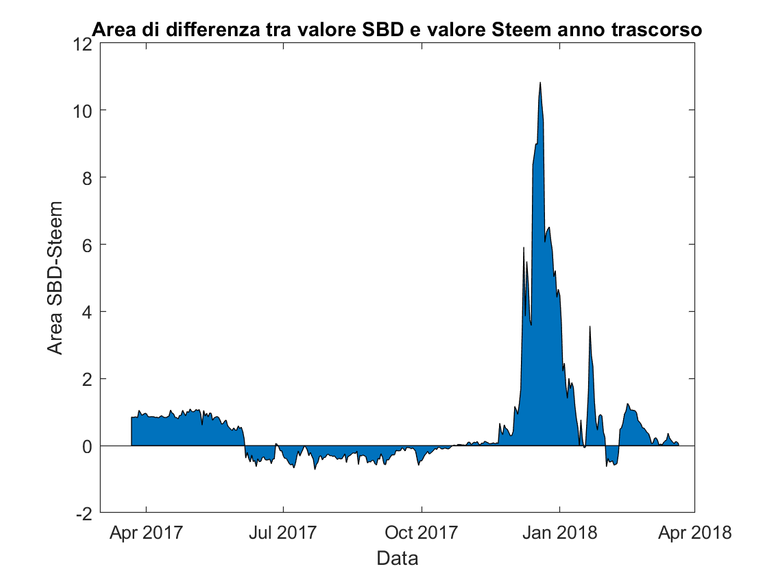
| area | Grafici rappresentativi di aree |
| pie | Grafici a torta |
| histogram | Istogrammi |
Potete trovare altrettanti strumenti grafici seguendo l'help in linea.
Matlab permette di personalizzare ad ogni modo la nostra visualizzazione grafica ma ricordiamoci che i vettori devono avere le stesse dimensioni!
Conclusioni
Abbiamo finalmente concluso la quarta lezione; nella successiva affronteremo il discorso matrici più nel dettaglio.
Volevo ringraziare @bjtcoin per aver dato un suo parere nella scorsa lezione. Spesso il confronto e anche la critica, se costruttiva, possono portare ad enormi miglioramenti!
Al fine di rendere quanto più didattico possibile il corso, ho deciso di fornirvi una parte della mia memoria cloud di Drive dove potete trovare delle cartelle con il materiale per poter eseguire autonomamente l'esercitazione proposta.
Basterà scaricare la cartella "Lesson 04" e selezionarla nella Current Folder.
Qui il link di condivisione della cartella Drive. In questa lezione saranno disponibili solamente le immagini e il file ".mat" dei dati.
Bibliografia e fonti
- Corso di Fondamenti di Matlab al Politecnico di Milano
- Corso online Matlab Fundamentals fornito da MathWorks
- L'esercitazione è creata interamente dal Team Daedevils
Fonti immagini:
- CCO licence
- Le restanti immagini sono create dal Team Daedevils e sono di sua proprietà
Indice
- Lezione 01 - Introduzione
- Lezione 02 - Importazione e tracciamento dati
- Lezione 03 - Incrementare l'automazione utilizzando gli script
 Immagine CC0 Creative Commons, si ringrazia @mrazura per il logo ITASTEM.
Immagine CC0 Creative Commons, si ringrazia @mrazura per il logo ITASTEM.CLICK HERE AND VOTE FOR "DAVINCI.WITNESS"
Being A SteemStem Member