
Salve a tutti!
Nella prima parte di questo articolo - Introduzione alla modellazione 3D Parametrica, Parte I - che ho pubblicato ieri, ho fornito una definizione ed una descrizione di questo metodo di modellazione, ho cercato di spiegarne i vantaggi ed i meccanismi, accennando ai suoi elementi di base, ovvero features e parametri.
Oggi analizzerò in modo più dettagliato proprio questi elementi di base, cercando di fornire una risposta chiara e comprensibile alle seguenti domande:
- Cosa sono le features o lavorazioni e perché sono tanto importanti?
- Cosa sono i parametri e a cosa servono?
Cosa sono le features e i parametri?
Parliamo innanzitutto delle features o lavorazioni: esse rappresentano una sorta di unità elementare di base della modellazione parametrica, poiché costituiscono tutte le operazioni che possiamo svolgere nel nostro ambiente di lavoro: dalle quattro operazioni fondamentali, ovvero estrusioni, rivoluzioni, loft e sweep, a lavorazioni quali forature, raccordi, smussi, svuotamenti, ecc.
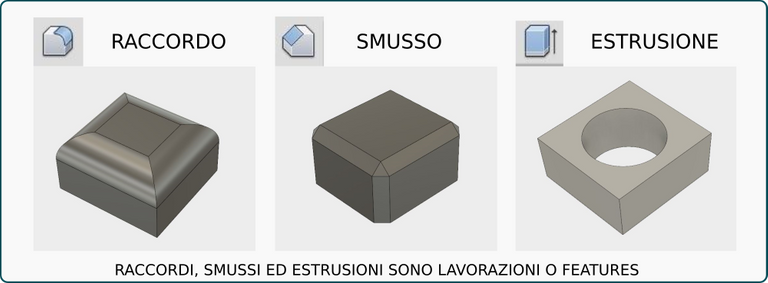
Ogni elemento del nostro spazio di lavoro viene realizzato a partire da una sequenza di lavorazioni (features) successive e ogni volta che eseguiamo una lavorazione, essa viene salvata dal software in una timeline, una sorta di narratore che ci permette a colpo d'occhio di leggere la sequenza di operazioni svolte dall'inizio alla fine, in ordine cronologico. Poiché le features sono a tutti gli effetti gli elementi di base della modellazione parametrica, ci si riferisce ad essa anche col nome di "feature-based modeling", ovvero modellazione basata sulle features.
Alcune features richiedono un disegno (2D o 3D) di base, altre invece sono applicate direttamente all'oggetto. Pertanto possiamo dividerle in due categorie: sketched-features le prime e applied-features le seconde. Esempi di sketched-features sono le quattro operazioni di base: estrusione, rivoluzione, sweep e loft; le features che non richiedono un disegno di base sono, tra le altre, i raccordi, gli smussi, svuotamenti o ispessimenti, ecc.
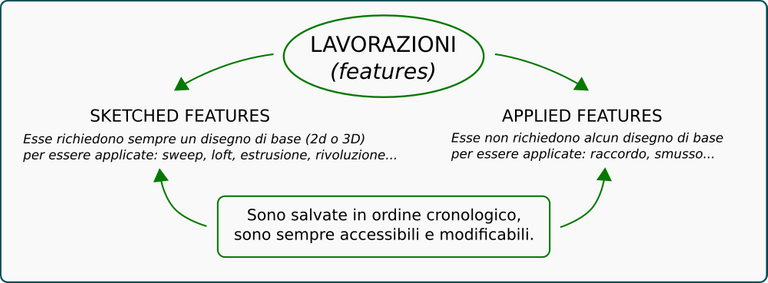
Le informazioni di base che definiscono le caratteristiche delle lavorazioni (il raggio di una circonferenza, la lunghezza di uno spigolo, l'altezza di un cilindro, l'angolo di una rivoluzione, ecc) sono, per usare una parola semplice, dei “numeri”, ovvero i cosiddetti parametri, che costituiscono la base matematica e anche le unità elementari delle features.
I parametri più "ovvi" sono le dimensioni, che possono apparire come quote su un disegno, ma possono anche essere nascoste. Un parametro può essere un numero (una funzione matematica o una misura), un valore testuale o booleano (sì/no, vero/falso). Software come Autodesk Inventor e Fusion360 raccolgono tutti i parametri di una parte o di un assieme di parti in una lista.
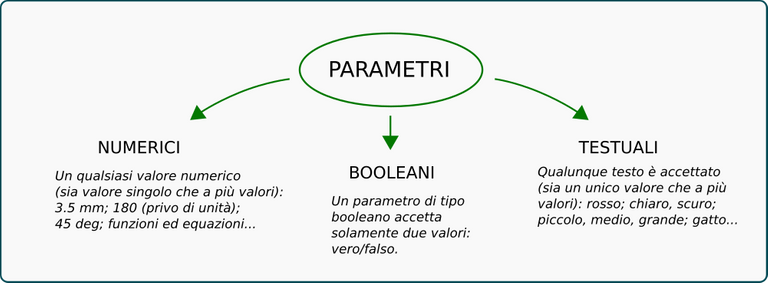
Si tratta di informazioni che hanno un legame bidirezionale con la geometria: i parametri dipendono dalla geometria e, al contempo, la geometria dipende dai parametri. Ciò significa che possiamo modificare le caratteristiche geometriche di un solido o di una superficie non solamente attraverso la manipolazione diretta della geometria, ma anche, forse più semplicemente, cambiando i valori di alcuni parametri rilevanti che troviamo sulla lista o sulla tabella generata dal software. In entrambi i casi, assisteremo ad una doppia modifica contemporanea: se modifichiamo un parametro otterremo una modifica della forma e se modifichiamo la geometria dall'ambiente di modellazione otterremo una modifica coerente del parametro correlato. Ecco perché parliamo di bidirezionalità.
Questo è un grande vantaggio della modellazione parametrica, perché permette in qualunque momento di avere pieno controllo delle misure e delle caratteristiche di un corpo solido o di superficie. Basta avere l'accortezza di rinominare i parametri significativi o commentarli nella lista, in modo da riconoscerli facilmente in qualunque momento.
Un'ultima considerazione, ma non per questo meno importante: quando modelliamo un oggetto utilizzando la modellazione 3D parametrica, il risultato della modellazione non è un oggetto ordinario ma costituisce un'intera classe di oggetti modificabili; è infatti possibile creare infinite combinazioni di parametri per generare potenzialmente infinite variazioni dello stesso oggetto. Ecco perché la modellazione parametrica è uno strumento considerato molto potente!
Lo so, vi ho costretto a leggere una montagna di teoria! Vi assicuro però che essa è estremamente importante per un primo approccio consapevole alla modellazione parametrica, per comprendere bene le sue basi ed il suo grande potenziale; in questo modo sarà più facile, in seguito, dedicarsi alla pratica!
Grazie mille a tutti per aver letto questo articolo!
Tornerò presto con un altro post, questa volta dedicato alle quattro operazioni fondamentali della modellazione 3D.
Nota: tutte le immagini presenti in questo articolo sono state realizzate dall'autore; il word cloud in apertura è stato ottenuto tramite uno strumento online gratuito e disponibile su Wordclouds.com
Se volete leggere la versione in inglese dei miei articoli introduttivi sulla modellazione parametrica, li trovate linkati di seguito:
1. Introduction to 3D parametric modeling - Part I
2. Introduction to 3D parametric modeling - Part II
Brava Fra argomento tosto! E complimenti anche x i corrispettivi in inglese :)
Grazie mille!
Questo post prezioso è stato scoperto dal Team OCD! Rispondi a questo commento se accetti e sei disposto/a a condividere il tuo post! Accettando questo, hai la possibilità di ricevere premi aggiuntivi e una delle tue foto in questo articolo può essere usata nel nostro compilation post! Puoi seguire @ocd per saperne di più sul progetto e vedere altri post preziosi! Ci sforziamo per la trasparenza.
This gem of a post was discovered by the OCD Team! Reply to this comment if you accept, and are willing to let us share your gem of a post! By accepting this, you have a chance to receive extra rewards and one of your photos in this article may be used in our compilation post! You can follow @ocd – learn more about the project and see other Gems! We strive for transparency.