[Mastering Ethereum] 3장 키와 주소

in #kr-dev • 6 years ago (edited)

modolee_logo
안녕하세요. 개발자 모도리입니다.
요즘 참여하고 있는 스터디에서 Mastering Ethereum 를 교재로 하여 매주 스터디를 진행하고 있습니다. 이번 주에 제가 맡은 부분을 정리해서 올립니다.

이더리움 키와 주소

  • 이더리움의 기반 기술 중 하나는 암호학이다.
  • 암호학(cryptography)는 그리스어로 비밀 글쓰기(secret writing)를 의미하지만, 암호학은 단순한 암호화 이 외의 더 많은 것들을 포함한다. - 디지털 서명(digital signature), 디지털 지문(digital fingerprints)
  • 이더리움 네트워크에 정보가 공개 될 때 암호화는 사용되지 않는다. 모든 정보를 누구나 볼 수 있다. 그래서 상태 업데이트가 올바르게 되었는지는와 합의가 이루어졌는지를 검증할 수 있다.
  • 이더리움에서 자산의 소유권을 제어하기 위한 개인 키와 주소에 사용되는 공개 키 암호화(PKC : public key cryptography)을 알아보자.

소개

  • 이더리움에는 EOA(Externally Owned Accounts), CA(Contract Accounts) 두 가지 종류의 계정이 존재한다. CA는 개인 키를 가지고 있지 않기 때문에, EOA에 대해서만 다루도록 한다.
  • 개인 키는 이더리움에서 사용자 간의 상호 작용에 있어 핵심적인 역할을 한다.
  • 계정 주소는 개인 키로 부터 얻어낼 수 있으며, 1개의 개인 키는 오직 1개의 계정 주소와 매핑된다.
  • 개인 키는 이더리움 시스템 내에서 직접적으로 사용되지 않는다. 즉, 이더리움 시스템에 직접적으로 전송되거나 저장되어 있지 않다.
  • 계정 주소와 디지털 서명 만이 전송되고 저장된다.
  • 자산의 접근과 제어는 개인 키를 이용해 만들어진 디지털 서명으로 이뤄진다.
  • 만약 누군가가 개인 키 복사본을 가지고 있다면, 동일하게 자산의 접근과 제어가 가능하다. 그러므로 안전한 개인 키 관리가 필요하다.
  • 이더리움과 같이 공개 키 암호화를 사용하는 시스템은 공개 키와 개인 키로 이루어진 키 쌍을 사용한다. 일반적으로 개인 키는 특별한 파일에 담겨 지갑 소프트웨어가 관리하고 있으므로, 사용자가 직접 보는 경우는 드물다.
    • 공개 키 : 은행의 계좌번호와 같아서, 다른 계정과의 식별을 위해서 사용된다.
    • 개인 키 : 은행의 비밀번호와 같아서, 계정을 제어할 수 있다.
  • 이더리움 전송 시 수신자는 이더리움 주소를 나타낸다. 일반적으로 공개 키를 통해 생성 된 주소이지만, 그렇지 않은 경우도 있다. (CA주소를 나타내기도 하며, CA는 개인 키를 가지고 있지 않다.)

공개 키 암호화와 암호화폐

공개 키 암호화의 발견

  • 공개 키 암호화(비대칭 키 암호화)은 현대의 정보 보안에 핵심이다.
  • 1970년대 전까지는 정부가 비밀로 지키고 있던 강력한 암호학 지식이 Martin Hellman, Whitfield Diffie, Ralph Merkle 세 사람에 의해 공개적으로 알려지게 되었다.

공개 키 암호화

  • 공개 키 암호화은 정보 보안을 위해 유일한 키를 사용한다.
    • 이 키는 특별한 속성을 갖는 수학 함수를 기반으로 한다.
    • 그냥 계산하시는 쉽지만, 역산은 힘들다.
    • 이 함수를 이용하면 수학의 법칙으로 안전이 보장되는 디지털 비밀과 위조할 수 없는 디지털 서명을 만들 수 있다.
  • 예를 들어 두 소수를 곱하는 것은 매우 쉬운 일이지만, 어떤 큰 수가 주어지고 곱해서 이 수를 만들 수 있는 두 소수를 구하는 것은 매우 어려운 일이다.
    • 8018009가 주어지고 곱해서 이 수를 만들 수 있는 두 소수를 찾는 것은 어렵다.
  • 이런 함수 중 몇 몇은 비밀 정보 일부가 주어지면 쉽게 풀 수 있다.
    • 앞의 수에서 한 소수가 2003이라는 것을 알려준다면, 8018009 ÷ 2003 = 4003 를 계산하여 다른 한 소수도 쉽게 구할 수 있다.
    • 이렇게 역산을 할 수 있는 함수의 비밀 정보가 없는 한 역산이 매우 힘든 함수를 trapdoor function이라고 부른다.

타원 곡선

  • 암호학에서 유용하게 사용되는 고급 수학 함수는 타원 곡선이다.
  • 타원 곡선의 산술, 곱셈 연산은 매우 단순하지만, 나눗셈은 거의 불가능하다.
  • 이것을 이산 로그 문제라고 부르며, 현재는 알려진 trapdoor function이 없다.
  • 타원 곡선 암호화는 현재 컴퓨터 시스템에 널리 사용되며 이더리움의 개인 키와 디지털 서명의 기초가 된다.

이더리움에서 공개키 암호화의 사용

  • 이더리움에서 개인 키 - 공개 키 쌍을 만들기 위해서 공개 키 암호화를 사용한다.
  • "쌍" 이라고 불리우는 이유는 공개 키가 개인 키로 부터 생성되기 때문이다.
  • 이것은 이더리움 계정과 계정의 자산을 제어할 수 있으며, 스마트 컨트랙트 이용 시 인증이 가능하다.
  • 디지털 서명은 어떤 메세지로도 만들 수 있는데, 이더리움에서는 메세지라는 정보와 개인 키를 이용해서 디지털 서명을 만든다.
  • 자산을 옮기거나 스마트 컨트랙트 실행을 위해 이더리움 네트워크에 트랜잭션을 보내기 위해서는 개인 키와 대응되는 디지털 서명이 있어야 한다.
  • 타원 곡선 알고리즘을 통하면 디지털 서명과 계정 주소, 트랜잭션 상세 내역을 맞춰 봄으로써 누구나 트랜잭션 검증이 가능하다.
  • 검증 과정에는 개인 키가 포함되지 않는다. 하지만 계정 주소를 생성한 공개 키와 쌍을 이루는 개인 키를 가진 사람만이 해당 메세지를 만들 수 있다는 것을 확실할 수 있습니다.
  • 이것이 공개 키 암호화의 "magic" 입니다.

TIP

  • 대부분의 지갑 구현체들은 개인 키, 공개 키 쌍을 모두 키 페어 형태로 저장한다. 하지만 개인 키를 통해서 공개 키를 생성할 수 있으므로, 개인 키가 저장되어 있어도 상관 없다.
  • 이더리움 프로토콜에 암호화 부분은 없다. 즉, 이더리움의 모든 메세지는 누구나 읽을 수 있다. 개인 키는 오직 트랜잭션 인증을 위한 디지털 서명을 만드는 데에 만 사용 된다.

개인 키(Private Keys)

  • 개인 키는 간단히 생각하면 랜덤하게 선택 된 숫자이다.
  • 개인 키를 소유하고 제어하는 것이 해당 키와 연결 된 이더리움 주소의 자산을 제어하는 데 핵심이다.
  • 그리고 또한 해당 이더리움 주소의 접근을 승인하는 스마트 컨트랙트에 접근할 수 있다.
  • 개인 키는 자산의 사용하는데 필요한 디지털 서명을 만드는데 사용된다.
  • 개인 키는 반드시 비밀로 잘 지켜야 한다. 개인 키가 제 3자에게 노출된다면, 그 사람 역시 개인 키 소유자와 동일하게 이더리움 계정의 자산과 스마트 컨트랙트들을 제어할 수 있게 된다.
  • 개인 키는 반드시 백업해 두어야 하고, 갑작스런 손실(분실)로 부터 보호되어야 한다. 개인 키를 잃게 된다면, 복구 할 수 없으며 자산 역시 영원히 잃게 된다.

랜덤 한 수로 부터 개인 키 생성하기

랜덤 소스

  • 개인 키를 만들기 위한 첫 단계는 안전한 엔트로피 소스 또는 랜덤성을 찾는 것이다.
  • 개인 키를 만들 때에는 반드시 1 ~ 2^{256} 사이의 숫자를 선택해야 한다.
  • 그 숫자를 고르는 방법이 예측 가능하거나 결정적(deterministic)이지 않다면 어떤 방법이든 상관없다.
  • 이더리움은 랜덤 한 256 bits를 만들기 위해 기본 운영체제의 난수 생성기(RNG : Random Number Generator)를 사용한다.
  • 보통 OS의 난수 생성기는 사람의 랜덤 소스에 의해 초기화 됩니다. 몇 초간 마우스를 마구잡이로 움직이거나 키보드를 마구잡이로 누르라고 요구하는게 이러한 이유입니다. 비트코인 주소 생성기
  • 다른 방법은 컴퓨터의 마이크 채널을 통해 들어 오는 우주 방사선 잡음을 이용하는 방법이다.

개인 키 범위

  • 조금 더 정밀하게 보자면, 개인 키는 0이 아닌 2^{256} (78자리 숫자로, 대략 1.158 * 10^{77} 정도) 이하의 숫자이다.
  • 정확한 숫자는 2^{256}와 앞 38 자리를 공유하며, 이더리움에서 사용하는 타원 곡선의 규칙에 의해 정의된다.
  • 개인 키 생성을 위해서는 랜덤 한 256 bits를 선택하고 유효한 범위인지 확인한다.
  • 프로그래밍 측면에서는 보통 매우 긴 랜덤 한 문자열(암호학적으로 안전한 랜덤성 소스로 부터 수집 된)을 Keccak-256 또는 SHA256(두 방법 모두 간편히 256-bits의 숫자를 만들어 냄 )과 같은 256-bits 해시 알고리즘에 넣어서 랜덤한 256-bits를 만들어 냅니다.
  • 만약 결과가 유효한 범위 안에 있다면 적합한 개인 키를 만들어 낸 것이고, 그렇지 않으면 다시 시도하면 된다.

개인 키 생성은 오프라인 작업

  • 개인 키 생성 과정은 이더리움 네트워크 또는 다른 어떤 외부와의 커뮤니케이션이 필요 하지 않아 오프라인으로 진행할 수 있다. (오프라인으로 하는 것을 추천)
  • 다른 누군가가 선택할 수 없는 숫자를 선택하려면 진~~짜 랜덤해야 한다.
  • 만약에 자신이 직접 숫자를 선택한다면, 다른 누군가도 시도해 볼 확률이 굉장히 높다. (그리고 이더가 털린다.)
  • 좋지 않은 난수 생성기(대부분의 프로그래밍 언어가 제공하는 pseudo-random rand() 함수와 같은 것)을 사용하는 것은 좋지 않은데, 그 이유는 제대로 된 난수 생성기에 비해 훨씬 더 분명하고 훨씬 더 복제하기 쉽다.
  • 온라인 계정의 비밀번호 처럼, 추측 불가능 해야 한다.
  • 다행스럽게도 개인 키를 기억할 필요가 없으므로 개인 키를 선택하는 최선의 방법(진정한 무작위성)을 취할 수 있습니다.

TIP
이더리움 개인 키 영역의 크기는 셀 수 없게 큰 숫자이다. 대략 10진수로 10^{77}, 77자리의 숫자이다. 비교를 해보자면, 볼 수 있는 우주가 10^{80}개의 원자를 포함하고 있다고 한다. 즉, 우주의 거의 모든 원자가 이더리움 계정을 가질 수 있을 만큼의 개인 키가 있는 것이다. 만약 랜덤 한 개인 키를 뽑았다면, 누구도 그 수를 추측할 수 있는 방법은 없다.

Warning
난수 생성을 위해 직접 코드를 작성하거나 프로그래밍 언어에서 제공하는 단순한 난수 생성기를 사용하지 마라. 필수적으로 충분한 엔트로피를 시드로 하는 암호학적으로 안전한 pseudo-random 숫자 생성기(CSPRNG - Cryptographically Secure Pseudo-Random Number Generator)를 사용하라. 난수 생성기의 문서를 공부하고 암호학적으로 안전한지 확실히 확인하라. CSPRNG 라이브러리의 올바른 구현은 키 보안에 굉장히 중요하다.

  • 아래는 랜덤하게 생성된 개인 키를 16진수 형태로 나타낸 것이다. (256 bits 가 64자리의 16진수로 표현되어 있다.):
    f8f8a2f43c8376ccb0871305060d7b27b0554d2cc72bccf41b2705608452f315

공개 키(Public Keys)

  • 이더리움의 공개 키는 타원 곡선 상의 한 점이다. 즉, 타원 곡선 방정식을 만족하는 x, y 좌표 쌍이다.
  • 단순히 말해서 이더리움 공개 키는 두 숫자이며 그것을 붙여서 사용합니다.
  • 이 두 숫자는 개인 키를 가지고 단 방향 계산을 해서 얻어진다.
  • 개인 키를 가지고 있으며 공개 키를 계산하는 것은 매우 쉽지만, 공개 키를 가지고 개인 키를 구하는 것은 불가능하다.

Warning
앞으로 수식들이 나올텐데, 당황하지 마라. 따라 오기 힘들다면, 다음 몇 섹션은 건너 뛸 수 있다. 당신 대신 수학을 해 줄 수 있는 툴과 라이브러리는 많다.

  • 공개 키는 개인 키를 이용한 타원 곡선 곱셈 계산을 통해 얻어지지만, 실질적으로 역산은 불가능하다.

  • K = k * G

    • k : 개인 키
    • G : 상수 점 (x, y). Generator Point
    • K : 공개 키
    • * : 일반 곱셈이 아닌 타원 곡선 상에서 일어나는 특별한 곱셈 연산자

  • K를 안다고 했을 때 가능한 모든 k를 brute-force로 시도한다고 했을 때 걸리는 시간은 우주가 허용하는 시간 보다 오래 걸릴 것이다.

  • 단순히 말하면 타원 곡선 상의 산술 연산은 일반적인 정수 산술 연산과 다르다.

  • 한 점(G)에 정수(k)배를 해서 다른 한 점(K)를 얻을 수 있다. 하지만 나눗셈과 같은 연산은 없다. 그래서 단순히 공개 키 K를 점 G로 나눈다고 해서 개인 키 k를 얻을 수 없다.

  • 이것이 공개 키 암호화와 암호화폐가 설명하고 있는 단방향 수학 함수이다.

TIP
타원 곡선 곱셈은 암호학자들이 "단 방향" 함수라고 말하는 것 중 하나이다. 정방향(곱셈)을 쉽게 할 수 있지만, 역방향(나눗셈)은 불가능하다. 개인 키 소유자는 쉽게 공개 키를 만들고 누구에게나 공유할 수 있지만, 누구도 공개 키를 가지고 개인 키를 계산할 수는 없다. 이 수학적 트릭이 위조할 수 없고 안전한 디지털 서명 기반이 되고, 디지털 서명은 이더리움 자산의 소유권을 증명하고 컨트랙트를 제어할 수 있다.

  • 개인 키로 부터 어떻게 공개 키를 만들어 내는 지 시연해 보기 전에 타원 곡선 암호화를 조금 더 자세히 살펴 보자.

타원 곡선 암호화 설명

  • 타원 곡선 암호화는 비대칭 (또는 공개 키 ) 암호화 종류로, 타원 곡선의 점에 덧셈과 곱셈으로 표현되는 이산 로그 문제를 기반으로 한다.
  • 아래 그림은 타원 곡선의 한 예로 이더리움에서 사용하는 타원 곡선과 비슷하다.

TIP
이더리움은 비트코인과 동일하게 secp256k1이라는 타원 곡선을 사용한다. 이 덕분에 많은 비트코인 라이브러리를 재사용 할 수 있다.

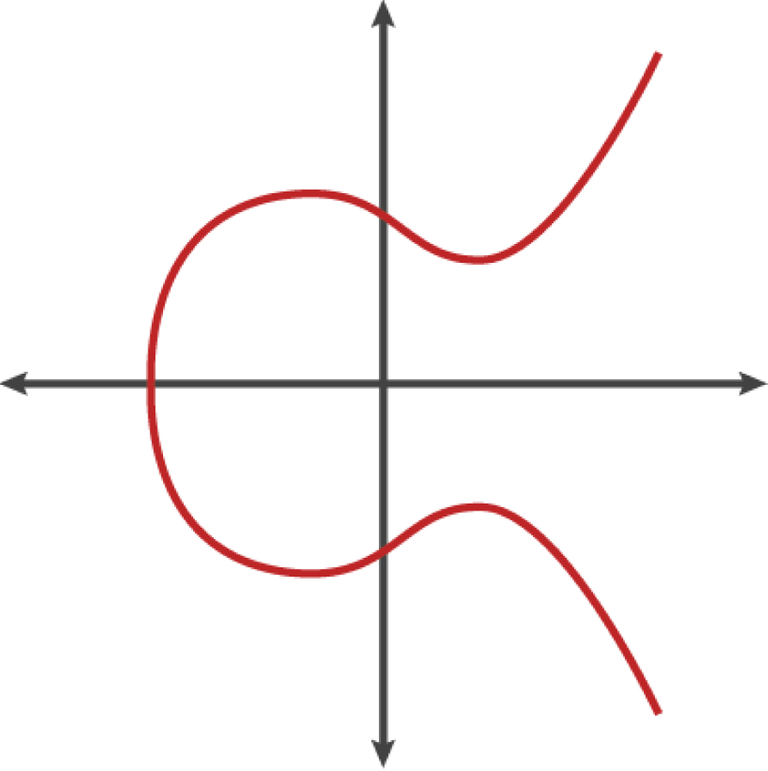
타원곡선_예

  • 이더리움은 NIST(US National Institute of Standards and Technology)에 의해 확립 된 secp256k1이라는 표준으로 정의 된 타원 곡선과 수학적 상수의 집합을 사용한다.
  • secp256k1 곡선은 타원 곡선을 만드는 아래 함수에 의해 정의된다.
  • y^2=(x^3+7) over (𝔽_p)
    or
  • y^2 mod p = (x^3+7) mod p
  • mod p 는 이 곡선이 소수 차수 p의 유한 체(finite field) 위에 있다는 것을 나타내며 𝔽_p 라고 쓴다.
  • p는 매우 큰 소수이다. p = 2^{256} – 2^{32} – 2^{9} – 2^{8} – 2^{7} – 2^{6} – 2^{4} – 1
  • 이 곡선은 실수가 아니라 소수 차수의 유한 체 상에 정의되기 때문에 시각화 하기 어려운 2차원의 흩어진 점들의 형태로 보여진다.
  • 하지만 수학적으로는 실수에서와 동일하다.
  • F(p), p=17 타원 곡선을 시각화 하면 다음과 같다.
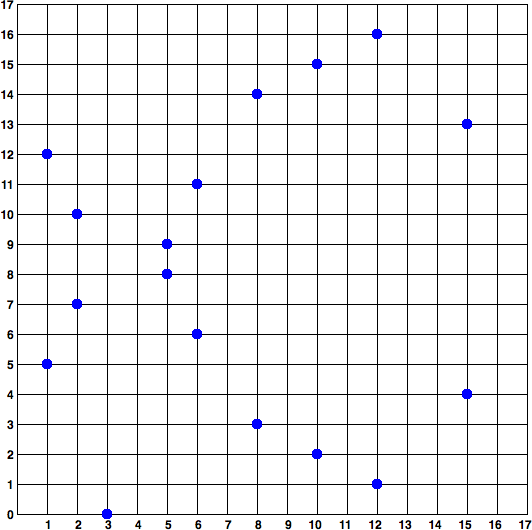
    샘플_타원곡선

secp256k1
secp256k1 - bitcoin wiki
secp256k1 실습
y^2=(x^3+ax+b) over (𝔽_p)

  • Curve
    • a = 0
    • b = 7
  • Field
    • p = 17

K = k * G

  • n : k (개인 키)
  • P : G (Generator Point)
  • Q = n * P : k * G (공개 키)
  • 아래 좌표 Q는 secp256k1 곡선 상의 한 점이다.
  • Q = (49790390825249384486033144355916864607616083520101638681403973749255924539515, 59574132161899900045862086493921015780032175291755807399284007721050341297360)
  • 파이썬을 이용해서 Q가 secp256k1 곡선 상의 점이라는 것을 검증할 수 있다.
  • y^2 mod p = (x^3+7) mod p 수식을 정리하면, (x^3+7 - y^2) mod p = 0 이 된다.
  • x, y에 Q의 좌표를 넣어서 계산해 보자.
  • 파이썬 연습장
p = 115792089237316195423570985008687907853269984665640564039457584007908834671663
x = 49790390825249384486033144355916864607616083520101638681403973749255924539515
y = 59574132161899900045862086493921015780032175291755807399284007721050341297360
result = (x ** 3 + 7 - y**2) % p
print(result)

실행 결과
0

타원 곡선 산술 연산

  • 많은 타원 곡선 수학은 우리가 학교에서 배웠던 정수 산술 연산과 상당히 비슷하게 보이고 동작한다.
  • 덧셈 연산자는 수직선 상에서 움직이는 대신에 곡선의 다른 점으로 움직인다.
  • 덧셈 연산자가 정의 되었다면, 곱셈 연산자도 정의할 수 있다. (곱셈은 덧셈을 반복하면 된다.)

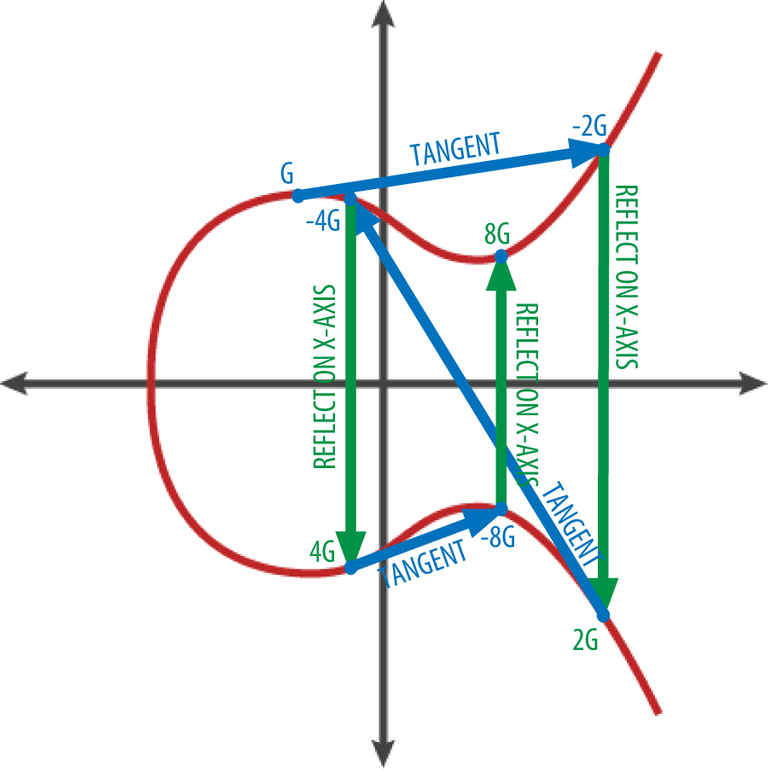
타원곡선_곱셈

공개 키 생성하기

  • 랜덤하게 생성 된 수 k (개인 키)를 미리 정의 된 곡선 상의 점 G(Generator Point)에 곱하면 곡선 상의 또 다른 점 K(공개 키)를 얻을 수 있습니다.
  • secp256k1 표준의 G가 정의되어 있으며, 항상 같은 G를 사용한다.

K = k * G

  • k : 개인 키
  • G : Generator Point (생성점?)
  • K : 공개 키
  • 모든 이더리움 사용자들이 항상 같은 G 를 사용하기 때문에, G에 개인 키 k를 곱하면 항상 같은 공개 키 K가 나온다.
  • k(개인 키)와 K(공개 키)는 고정 된 관계를 가지고 있지만, k에서 K를 구하는 단 방향으로의 계산만 가능하다.
  • 그래서 이더리움 주소(공개 키로 부터 생성 된)를 개인 키 노출 없이 누구나와 공유할 수 있다.

예제 용 개인 키
f8f8a2f43c8376ccb0871305060d7b27b0554d2cc72bccf41b2705608452f315

  • 위의 개인 키를 이용해서 공개 키를 만들어 보자.
  • K = f8f8a2f43c8376ccb0871305060d7b27b0554d2cc72bccf41b2705608452f315 * G
  • K 는 2차원 상의 한 점이다. K = (x, y)

개인 키로 얻은 2차원 점 K
x = 6e145ccef1033dea239875dd00dfb4fee6e3348b84985c92f103444683bae07b
y = 83b5c38e5e2b0c8529d7fa3f64d46daa1ece2d9ac14cab9477d042c84c32ccd0

  • 이더리움의 공개 키는 130자의 16진수(65 bytes) 표현 된다.
  • Standards for Efficient Cryptography (SEC1)에서는 타원 곡선 상의 점을 식별하는데 사용할 수 있는 4가지 prefix를 정의했다.
| Prefix | Meaning                      | Length (bytes counting prefix)
| 0x00   | Point at Infinity            | 1
| 0x04   | Uncompressed Point           | 65
| 0x02   | Compressed Point with even Y | 33
| 0x03   | Compressed Point with odd Y  | 33
  • 이더리움은 압축 안된 공개 키만 사용하여, 04 prefix만 사용한다.
    04 + X-coordinate (32 bytes/64 hex) + Y-coordinate (32 bytes/64 hex)
  • 예제 용 개인 키로 만든 공개 키는 다음과 같다.
    046e145ccef1033dea239875dd00dfb4fee6e3348b84985c92f103444683bae07b83b5c38e5e2b0c8529d7fa3f64d46daa1ece2d9ac14cab9477d042c84c32ccd0

타원 곡선 라이브러리

  • 암호화폐 관련 된 프로젝트에서 사용되는 secp256k1 타원 곡선의 구현체가 몇 가지 있다.

OpenSSL

  • OpenSSL 라이브러리는 secp256k1의 모든 구현을 포함하여, 포괄적인 암호학적 기본 요소(primitives)를 제공한다.
  • 예를 들어 공개 키를 만들어 내기 위해 EC_POINT_mul()를 사용할 수 있다.
  • https://www.openssl.org/

libsecp256k1

  • 비트코인 코어의 libsecp256k1은 secp256k1과 다른 암호학적 기본 요소의 C언어 구현체이다.
  • libsecp256k1의 타원 곡선 암호화는 비트코인 코어의 OpenSSL을 대체하기 위해서 스크래치부터 구현되었다.
  • 성능과 보안 모두 뛰어나다.
  • https://github.com/bitcoin-core/secp256k1

암호화 해시 함수

암호화 해시 함수의 5가지 주요 속성

  • Determinism

    • 동일한 입력 메세지는 항상 같은 해시 출력을 만든다.

  • Verifiability

    • 메세지의 해시 계산이 효율적이다. (선형 복잡도)

  • Uncorrelated

    • 원본 메세지와 출력 해시를 연관 지을 수 없도록 입력 메세지의 매우 작은 부분이 변경되어도 해시 출력의 많은 부분이 변경되어야 한다.

  • Irreversibility

    • 해시 출력을 통해서 입력 메세지를 계산하는 것은 불가능합니다. brute-force로 가능한 모든 메세지를 찾는 것과 같습니다.

  • Collision Protection

    • 두 개의 다른 입력 메세지가 동일한 해시 출력을 만들 수 없어야 한다.
    • 해시 충돌에 대한 저항은 이더리움에서 디지털 서명 위조를 피하기 위해 중요합니다.

  • 이러한 속성들 덕분에 암호화 해시 함수가 다양한 보안 프로그램에서 유용하게 사용된다.

    • Data fingerprinting
    • Message integrity (error detection)
    • Proof-of-Work
    • Authentication (password hashing and key stretching)
    • Pseudo-random number generators
    • Message commitment (commit–reveal mechanisms)
    • Unique identifiers

이더리움의 암호화 해시 함수 - Keccak-256

  • Keccak-256은 2007년에 National Institute of Science and Technology(NIST)에서 주최한 SHA-3 암호화 해시 함수 경연에 후보로 설계되었다.
  • Keccak이 우승하였고, 2015년에 Federal Information Processing Standard (FIPS) 202로 표준화 되었다.
  • 이더리움 개발 중에는 아직 NIST 표준이 확정되지 않았고, NIST가 효율성을 향상시키기 위해서 코드를 수정했다.
  • 수정한 코드의 결함이 발생해서 표준화가 늦어졌다.
  • 이더리움 재단에서는 NIST가 수정한 SHA-3 표준 보다는 원본 Keccak 알고리즘을 구현하기로 결정했다.
  • 이더리움에서 사용하는 Keccak-256과 최종 확정 된 표준 FIP-202 SHA-3의 차이 때문에 혼란을 일으킨다. ERC-59에서 모든 코드와 OPCODE에 있는 sha3 다시 네이밍하기 위해 나눈 흔적을 찾아 볼 수 있다.

사용하고 있는 해시 함수가 어떤 것일까?

  • 이더리움 코드에 SHA-3, Keccak-256을 혼용해서 사용하고 있긴 하지만, Keccak-256을 사용한다.
  • 실제로 공백 해시를 통해서 확인할 수 있습니다.
Keccak256("") =
c5d2460186f7233c927e7db2dcc703c0e500b653ca82273b7bfad8045d85a470

SHA3("") =
a7ffc6f8bf1ed76651c14756a061d662f580ff4de43b49fa82d80a4b80f8434a

이더리움 주소

  • 이더리움 주소는 공개 키 또는 컨트랙트에 Keccak-256 해시 함수를 적용하여 만들어 낸 유일한 식별자이다.
  • 이전 예제에서 사용했던 개인 키, 공개 키를 다시 가져와보자.
  • 개인 키 k :
    k = f8f8a2f43c8376ccb0871305060d7b27b0554d2cc72bccf41b2705608452f315
  • 공개 키 K :
    K = 6e145ccef1033dea239875dd00dfb4fee6e3348b84985c92f103444683bae07b83b5c38e5e2b0c8529d7fa3f64d46daa1ece2d9ac14cab9477d042c84c32ccd0

Warning
주소를 계산할 때 사용하는 공개 키 형식은 prefix 04를 포함하지 않는다.

  • Keccak-256을 이용한 공개 키 K의 해시 :
    Keccak256(K) = 2a5bc342ed616b5ba5732269001d3f1ef827552ae1114027bd3ecf1f086ba0f9

Question

  • 실제로 공개 키 K를 Keccak-256 해시 함수에 넣어서 돌려보면 다른 값이 나오는데 왜 그런가??? 더 찾아보기
    6e145ccef1033dea239875dd00dfb4fee6e3348b84985c92f103444683bae07b83b5c38e5e2b0c8529d7fa3f64d46daa1ece2d9ac14cab9477d042c84c32ccd0 이 형태 그대로 Keccak256에 입력으로 집어 넣는게 아닌가???
    53a07bd0be78dd08f3505b0f4daafc5d8dc848ca07a8b87f24129615789912ff
  • https://keccak-256.cloxy.net/
  • https://emn178.github.io/online-tools/keccak_256.html
  • 아래 소개 되는 helpeth를 이용하면 위와 같은 결과가 나오는데 그냥 직접 Keccak256을 돌리면 아래 값이 나온다.
    ./helpeth keyDetails -p 0xf8f8a2f43c8376ccb0871305060d7b27b0554d2cc72bccf41b2705608452f315
  • 그런데 여기서 제공하는 keccak256을 돌리면 또 정상적으로 나오는데, 16진수 인코딩의 문제가 아닌가 생각된다.
  • 입력 데이터에 prefix "0x"를 안 붙였을 때
    ./helpeth keccak256 6e145ccef1033dea239875dd00dfb4fee6e3348b84985c92f103444683bae07b83b5c38e5e2b0c8529d7fa3f64d46daa1ece2d9ac14cab9477d042c84c32ccd0 -> 53a07bd0be78dd08f3505b0f4daafc5d8dc848ca07a8b87f24129615789912ff
  • 입력 데이터에 prefix "0x"를 붙였을 때
    ./helpeth keccak256 0x6e145ccef1033dea239875dd00dfb4fee6e3348b84985c92f103444683bae07b83b5c38e5e2b0c8529d7fa3f64d46daa1ece2d9ac14cab9477d042c84c32ccd0 -> 2a5bc342ed616b5ba5732269001d3f1ef827552ae1114027bd3ecf1f086ba0f9

  • 해시 결과 중에서 마지막 20 bytes (least significant bytes)가 바로 이더리움 주소이다.
    001d3f1ef827552ae1114027bd3ecf1f086ba0f9

  • 대부분의 이더리움 주소는 16진수로 인코딩 되었다고 표시하는 prefix "0x"를 붙이고 있다.
    0x001d3f1ef827552ae1114027bd3ecf1f086ba0f9

이더리움 주소 형식

  • 이더리움 주소는 공개 키의 Keccak-256 해시 값 중 마지막 20 bytes를 16진수로 표현한 것이다.
  • 주소 자체에 체크섬을 포함하고 있는 비트코인 주소와 다르게 이더리움 주소는 별도의 체크섬이 없는 raw 16진수이다.
  • 상위 레이어에서 체크섬을 포함하려고 하는데, ENS 같은 상위 레이어의 개발이 초기에 기대했던 것 보다 매~~우 느려서 대안을 ICAP 같은 인코딩이 지갑 개발자들이 사용하게 되었다.

Inter Exchange Client Address Protocol (ICAP)

  • International Bank Account Number (IBAN) 와 부분적으로 호환되는 형식
  • 표현하는 방식은 Direct, Basic, Indirect 3가지 있다.
  • 현재 많이 사용되고 있지 않기 때문에, 자세한 내용은 다루지 않겠다.
  • 자세한 내용은 공식 위키를 참고 바람

Hex encoding with checksum in capitalization (EIP-55)

  • ICAP와 ENS의 늦은 개발 때문에, EIP-55로 다른 표준이 제안되었다.

  • EIP-55는 16진수 주소 중 일부를 대문자화하여 구버전과 호환되는 이더리움 주소 체크섬을 제공한다.

  • 이더리움 주소는 대소문자 구분없이 사용할 수 있다는 점을 이용한 아이디어이다.

  • 일반 이더리움 주소
    0x001d3f1ef827552ae1114027bd3ecf1f086ba0f9

  • EIP-55 적용한 주소
    0x001d3F1ef827552Ae1114027BD3ECF1f086bA0F9

  • 두 주소의 차이점은 중간 중간 대문자로 변경된 영문자가 보인다는 것이다.

  • EIP-55 적용하는 방법

  • prefix "0x"를 제외한 소문자로 된 주소의 해시 값을 구한다.

Keccak256("001d3f1ef827552ae1114027bd3ecf1f086ba0f9")
23a69c1653e4ebbb619b0b2cb8a9bad49892a8b9695d9a19d8f673ca991deae1
  • 주소와 주소 해시 값의 같은 자리 문자끼리 비교한다.
Address: 001d3f1ef827552ae1114027bd3ecf1f086ba0f9
Hash   : 23a69c1653e4ebbb619b0b2cb8a9bad49892a8b9...
  • 만약 해시 값이 0x8과 같거나 큰 경우 대문자로 바꿔준다.
Address: 001d3F1ef827552Ae1114027BD3ECF1f086bA0F9
Hash   : 23a69c1653e4ebbb619b0b2cb8a9bad49892a8b9...


  • 에러 검출하기
  • 주소 0x001d3F1ef827552Ae1114027BD3ECF1f086bA0F9 의 마지막 두번째 문자 F를 E로 잘못 입력 한 경우
  • 주소는 0x001d3F1ef827552Ae1114027BD3ECF1f086bA0E9가 되고, 해시 값은 다음과 같다.
Keccak256("001d3f1ef827552ae1114027bd3ecf1f086ba0e9")
5429b5d9460122fb4b11af9cb88b7bb76d8928862e0a57d46dd18dd8e08a6927
  • EIP-55 조건에 맞게 대문자화 되었는지 확인해 본다.
001d3F1ef827552Ae1114027BD3ECF1f086bA0E9
5429b5d9460122fb4b11af9cb88b7bb76d892886...
  • 뒤에서 4번째 문자 A와 매칭되는 해시 값은 2인데 대문자화 되어 있으니, 뭔가 잘못 된 것이다! (다른 문자들도 다른 것이 더 있다.)

Key, Transaction 관리 툴 helpeth

  • https://github.com/ethereumjs/helpeth
  • 다양한 기능을 제공하지만 여기에선 개인 키를 넣어서 공개 키, 주소, ICAP주소, EIP-55 체크섬 주소 정보를 얻을 수 있는 명령을 소개한다.
  • 설치를 위해서는 npm이 필요하다.
  • 설치하기
    git clone https://github.com/ethereumjs/helpeth.git
    cd helpeth
  • 실행하기
    npm install
    helpeth keyDetails -p 0xf8f8a2f43c8376ccb0871305060d7b27b0554d2cc72bccf41b2705608452f
  • 실행 결과
    Address: 0x001d3f1ef827552ae1114027bd3ecf1f086ba0f9
    Address (checksum): 0x001d3F1ef827552Ae1114027BD3ECF1f086bA0F9
    ICAP: XE60 HAMI CDXS V5QX VJA7 TJW4 7Q9C HWKJ D
    Public key: 0x6e145ccef1033dea239875dd00dfb4fee6e3348b84985c92f103444683bae07b83b5c38e5e2b0c8529d7fa3f64d46daa1ece2d9ac14cab9477d042c84c32ccd0

결론

  • 이더리움의 공개 키, 개인 키 사용을 중심으로 공개 키 암호화에 대해서 알아보고, 이더리움 주소 생성과 검증에 사용되는 해시 함수와 같은 암호학적 도구들을 사용해 봤다.
  • 그리고 디지털 서명과 어떻게 개인 키를 드러내지 않고 개인 키의 소유권을 주장할 수 있는지도 살펴봤다.
  • Wallets 챕터에서는 이런 것과 더불어 지갑이 어떻게 키들을 관리하는지 살펴보겠다.

참고 자료

#kr #ethereum #mastering-ethereum #keccak256
6 years ago in #kr-dev by
$0.14
  • Past Payouts $0.14
  • - Author $0.11
  • - Curators $0.03
10 votes
Reply 5
Sort:  
  • Trending
    • [-]
     6 years ago  

    오! 대단하십니다!

    [-]
     6 years ago (edited) 

    감사합니다! ^^

    $0.00
      Reply
      [-]
       6 years ago  

      저보다 정리를 더 잘해주셨네요.ㅎㅎ

      $0.00
        Reply
        [-]
         6 years ago  

        먼저 정리해 주신 덕분에 도움 많이 됐습니다! ^^

        $0.00
          Reply
          [-]
           6 years ago (edited) 
          • 개인 키 : 256 bits (32 bytes)
          • 공개 키 : 520 bits (65 bytes) -> 실제로 해시에는 64bytes만 사용
          • 주소 : 160 bits (20 bytes)

          주소의 표현할 수 있는 범위가 개인 키, 공개 키 보다 좁으니 서로 다른 개인 키에서 동일한 주소를 생성할 수도 있지 않느냐 라는 질문을 받았습니다.

          그래서 구글링을 해봤는데, 가능성은 있지만 그 가능성이 매우 희박하다라고 답변이 달려 있습니다. 물론 이 글은 비트코인 관련 질문이긴 하지만 이더리움도 동일하게 적용됩니다.

          https://bitcointalk.org/index.php?topic=566319.msg6208311#msg6208311

          "하루 동안 상어한테 물리고, 버스에 치이고, 총 맞고, 번개를 맞은 다음에 복권에 당첨 될 정도의 확률이다" 라고 하네요 ㅋㅋㅋ

          $0.00
            Reply