1을 무한히 곱하면 그것은 무엇일까?
1을 유한번 곱하면 답은 1이다. 근데 1을 무한번 곱하면 1일까? [참고로 1을 무한번 더하면 무한대라는 것은 쉽게 짐작 가능하다.]
절대값이 1보다 큰 수의 경우에는 무한번 곱하면 무한대가 된다. 작은 수의 경우 무한번 곱하면 0이 될 것이다. 그러나 절대값이 1인 경우에는 어떻게 될까?
정답은 무한대이다. 사실 이는 로그의 정의와 관련이 있다. 1의 무한번 곱을 A라 가정하고 로그를 취해보면 유한한 것의 무한번 덧셈이 되어 무한이 된다.
[과연? @blockchainstudio 님이 댓글로 이것이 잘못된 것이라는 것을 보여주셨다. log(1) =0 이기 때문에 사실 무한대 0 (이 0은 exact 한 값) 즉 0을 무한번 더해도 0이니 0이 된다. 이런 ㅋㅋ 초등학생(?) 친구에게 잘못 알려준게 되버렸군 ㅋㅋㅋ;
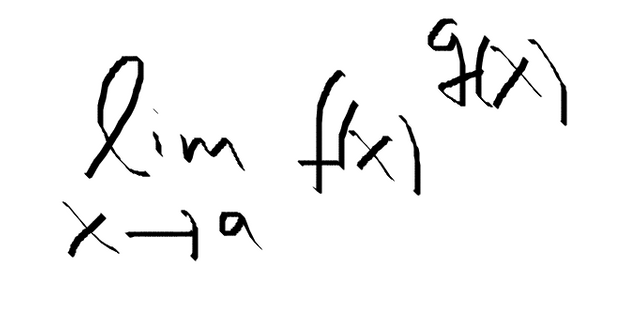
이런 경우의 문제에서는 Indeterminate 즉 부정형으로 정의가 잘 되지 않는다. 비슷한 질문을 0^0 에도 할 수 있겠다. 이 두 0이 모두 exact 한 값이라면 어떻게 지수의 0 을 정의하는 가에 따라 달라지겠지만, 0으로 가는 극한값인 경우에 똑같은 문제가 발생한다.* 더 자세히 알고 싶다면 위키 링크를 참조
즉 극한을 취할 때 그 1이 정말 exact 한 1과 0인지 아니면 극한값이 1이나 0으로 가는지가 중요하다.
좀 더 생각해보고 글을 쓸껄 ㅋㅋㅋ 이런 ㅋㅋㅋ 실수가 박제되어 버렸군 ㅋㅋㅋㅋ
그래도 이렇게 실수했으니 다시는 까먹지 않을듯!!!
]
추후에 무한과 유한에 대한 이야기를 한번 정리해 보는 시간을 가져봐야 겠다. 잠깐 편의점에 햄버거와 라면을 사러 가는 동안 엘레베이터에서 만난 한 친구의 질문에 이런 포스팅을 남긴다. [Sorry]
[* 흠 log1 의 값을 생각 안 한 것을 둘째 치고, 내 머릿속에 Product에 관해서 Arbitrary product 와 finite product 를 생각하면서 Product topology 를 생각해서 그 차이를 고려한다고 하면서 이런 사단이 일어난듯 싶다.* ㅠㅠ 너무 오랜만에 테크닉컬한 것이 아닌 이런 것을 생각해서 그런가? ㅋㅋㅋ ]
재미있는 질문이네요. 그런데 1+와 같은 극한값이 아닌이상 1 무한번 곱하면 여전히 1이 되긴 합니다.
말씀해주신 log로 생각해도 log1=0이므로 무한번 더해도 0이고 그러니 여전히 A=1.
흠 ㅋㅋㅋ
@blockchainstudio 님의 말이 맞습니다.
제가 다른 문제랑 헷갈렸네요
이런 형태에서 f->1, g-> 무한대로 갈 때의 문제에서는 부정형(Indeterminate) 이고 정확히 숫자를 가졌을 때는 1이 되는게 맞는것 같습니다.
이런; ㅋㅋㅋ
감사합니다^^ 무한대는 사실 헷갈릴 수밖에 없는 개념인 것 같아요.
1을 무한대 곱하면 무한대이군요. 기준을 무한대에 두면 이해가 되네요. ㅎ
이런 @zzan.co8 님 제가 헷갈렸네요 ㅋㅋㅋㅋ 아래 @blockchainstudio 님이 정정해 주셨어요
Hi @beoped!
Your UA account score is currently 3.636 which ranks you at #6287 across all Steem accounts.
Your rank has dropped 507 places in the last three days (old rank 5780).Your post was upvoted by @steem-ua, new Steem dApp, using UserAuthority for algorithmic post curation!
In our last Algorithmic Curation Round, consisting of 93 contributions, your post is ranked at #39.
Evaluation of your UA score:
Feel free to join our @steem-ua Discord server