Introduction
저번시간에 어떤 집합 위에 정의된 equivalence relation의 개념과 예시에 대해 배웠습니다. 오늘은 지난번에 언급했던 quotient set 에 대해서 알아보고, 구체적인 예시를 들어보겠습니다. 그리고 Group의 Example들을 다룰 때 들었던 예시 ℤ/nℤ 를 다시 설명해 보겠습니다.
우선, S 를 set 이라고 두고 ~를 equivalence relation on S 라고 하겠습니다. any 원소 x∈S에 대하여 Equivalence class 라는 것을 정의 하겠습니다:
Definition
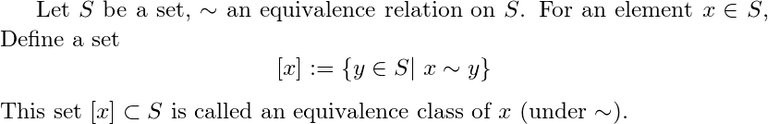
다시 말해서, x∈S의 equivalence class [x]는 S의 원소 중에서 x와 ~로 relation이 있는 것들을 원소로 갖는 집합입니다. 나은 이해를 위해 예시를 들어보겠습니다:
Example
ℤ 위에서 equivalence relation 을 생각할 수 있는데 대표적인 예가 저번 글에서 말씀드렸던 ≡ (mod n) 입니다 (n은 정수).
보다 구체적으로 보기 위해서 n=5라고 합시다. 그러면 equivalence classes 들은 다음과 같이 됩니다:
······
[0]={···,-10,-5,0,5,10,···}=5ℤ
[1]={···,-9,-4,1,6,11,···}=1+5ℤ
[2]={···,-8,-3,2,7,12···}=2+5ℤ
[3]={···,-7,-2,3,8,13···}=3+5ℤ
[4]={···,-6,-1,4,9,14,···}=4+5ℤ
······
이것은 equivalence class의 정의로 부터 쉽게 알 수 있습니다 (체크해 보세요).
[a] 의 원소는 a≡b (mod 5)인 모든 b∈ℤ 입니다. 다시 말해서, a와 b를 5로 나누었을 때 나머지가 같은 정수 b 들을 원소로 갖는다는 말입니다.
이 예시로 알 수 있는 놀라운 점이 있습니다:
≡ (mod 5) 에 대하여 다른 원소 a,b∈ℤ 들에 대해서는 [a] 와 [b]가 다르구요, 심지어 [a]와 [b]의 교집합이 공집합 입니다.
≡ (mod 5) 에 대하여 같은 원소 a,b∈ℤ 들에 대해서는 [a]와 [b]가 같습니다.
모든 a∈ℤ에 대하여 [a]를 합집합 하면 전체 집합 S 가 됩니다.
이를 일반적인 set S 와 equivalence relation ~ on S 에도 생각해 볼 수 있습니다:
Proposition
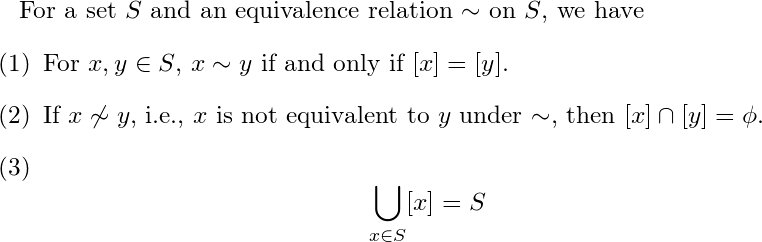
이러한 성질을 equivalence classes 가 S의 partition 을 만든다고 합니다. (the equivalence classes form a partition of S)
이 proposition을 다음과 같이 증명할 수 있습니다:
Proof
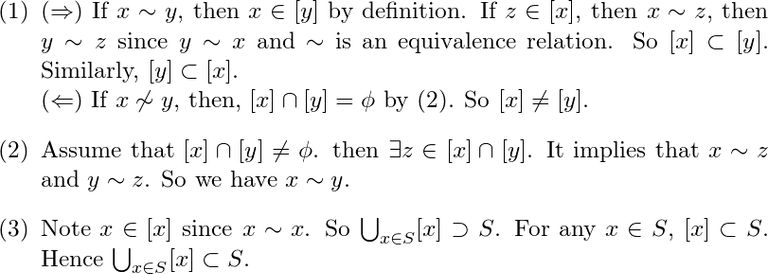
자, 그럼 집합 S의 partition이라는게 무슨 의미일까요? 말 그대로 S를 쪼갠다는 의미입니다. 위의 예시 ℤ에서 the equivalence classes under ≡ (mod 5) 가 ℤ를 5등분으로 쪼개는 것을 알 수 있습니다:
ℤ=[0]∪[1]∪[2]∪[3]∪[4]
마지막으로 대망의 quotient set을 정의하겠습니다:
Definition

그러면 앞의 Proposition에 의해서 S/~ 는 S 의 partition이 됩니다.
ex) ℤ/≡ (mod 5)={[0],[1],[2],[3],[4]}
그리고 ℤ/5ℤ=ℤ/≡ (mod 5) 임을 알 수 있습니다 (as a set).
일반적인 정수 n에 대해서도 ℤ/nℤ=ℤ/≡ (mod n) 입니다.
글을 마치며
다음시간에는 quotient set 의 중요한 예시들을 소개하겠습니다. 읽어주셔서 감사합니다.
와...제가 읽어도 이해할 수 없는 내용들이라.ㅠ
아무튼 편안한 저녁 되시길 바라겠습니다.
네. 읽어주셔서 감사드립니다~
짱짱맨은 스티밋이 좋아요^^ 즐거운 스티밋 행복한하루 보내세요!
네 감사합니다~ 즐거운 스티밋 되세요~!
술마시고 보려니 따라가기 힘드네요 ㅋㅋ 정신차리고 다시 복습해야겠습니다.
다이어트 중이라.. 금주.. 저도 술마시고 싶네요 ㅠ 읽어주셔서 감사합니다~
일일이 tex로 쳐서 이미지로 만든다음에 올리시는 것이라면, 무척 노동이겠습니다. 개념부터 차근차근 적어주심에 감사합니다. 독자층이 많지는 않을 것 같아서 그게 좀 걱정입니다.
제가 tex는 지겹도록 많이 쳐봐서 힘들지는 않네요.. 애초에 순수수학이라 많은 독자층은 기대 안했지만 그래도 봐주시는 분들이 계셔서 힘이 납니다!
꾸준히 쓰다보면 독자층도 꾸준히 늘지 않을까 싶네요.
네. 응원드립니다. 개인적으로 TDA도 최근에 관심있게 살펴보고 있어서, 아마 관련된 부분이 나오면 제가 질문을 드릴 수도 있을 것 같습니다.
여담이지만, 순수수학과 더불어, (일반인들을 위한) 약간의 (쉽게 풀어쓴) 현재의 학문적 동향이나 숨겨진 비사 같은 것을 적어보셔도 괜찮을 듯 싶습니다. 부담드리는 것이 절대 아니니, 그냥 참고만 하시면 좋겠습니다. :)
제가 TDA는 잘 모르지만, 관련 수학 지식들에 대해서는 도움을 드릴수도 있겠네요. (대수위상이라던지..)
일반인들도 읽을만한 글도 한번 쓰도록 해 보겠습니다. 코멘트 감사합니다!